Skip to main content
SpringerLink
Log in

Non-Linear Analysis of Axially Loaded Piles Using “t–z” and “q–z” Curves

  • State-of-the-Art Review
  • Published:
Geotechnical and Geological Engineering Aims and scope Submit manuscript

Abstract

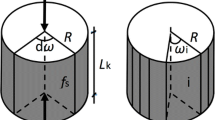
In the present work, the behaviour of a single pile submitted to axial loading is analyzed. Namely, we examine the static stiffness coefficient at the head of a flexible pile, vertically embedded in a homogeneous or multilayer soil of random geometry and mechanical properties. To solve the problem, an analytical closed form solution is developed, based on Winkler’s theory. The model is used in combination with suitable shape functions, which describe reliably the vertical movement of the pile with depth. By choosing the appropriate shape functions along with “t–z” and “q–z” curves and following an iterative process, a relatively accurate estimation of the vertical displacement at the head of the pile can be achieved. Unlike traditional numerical solutions, the proposed method does not require discretization of the pile into finite elements (and afterwards resolution of a system of linear equations of high order) but only discretization in sections aiming integration with depth.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12

Similar content being viewed by others

References

  • American Petroleum Institute (1993) Recommended practice for planning, designing and constructing fixed offshore platforms–load and resistance factor design, API Recommended practice 2A-LRFD, 1st edition

  • Bustamante M, Frank R (1997) Design of axially loaded piles: French practice. In: De Cock F, Legrand C (eds) Design of axially loaded piles: European practice. Balkema, Rotterdam, pp 161–175

    Google Scholar 

  • Coyle HM, Reese LC (1966) Load transfer for axially-loaded piles in clay. J Soil Mech Found Div ASCE 92(SM2):1–26

    Google Scholar 

  • Fahey M, Carter JP (1993) A finite element study of the pressuremeter test in sand using a nonlinear elastic plastic model. Can Geotech J 30:348–362

    Article  Google Scholar 

  • Foi A-MG (2014) Non-linear analysis of axially loaded piles using ‘‘t–z’’ curves. MSc Dissertation, University of Patras, [in Greek]

  • Geognosi SA (1995) Assessment of results of a load test for a pile of diameter 800 mm. Thessaloniki (Greece), [in Greek]

  • Kraft LM, Ray RP, Kagawa T (1981) Theoretical t–z curves. J Geotech Eng Div ASCE 107(GT11):1543–1561

    Google Scholar 

  • Mylonakis G (1995) Contributions to static and seismic analysis of piles and pile-supported bridge piers. PhD Dissertation, University of New York, Buffalo

    Google Scholar 

  • Mylonakis G, Gazetas G (1998) Settlement and additional internal forces of grouped piles in layered soil. Geotechnique 48(1):55–72

    Article  Google Scholar 

  • Novak M (1974) Dynamic stiffness and damping of piles. Can Geotech J 11(4):574–598

    Article  Google Scholar 

  • Psaroudakis E, Mylonakis G, Klimis N and Foi A-M (2014) Non-linear analysis of axially loaded piles using “t–z” curves. 7th Pan-Hellenic Congress of Geomechanics, Athens [in Greek]

  • Rajapakse RKND (1990) Response of axially loaded elastic pile in a Gibson soil. Geotechnique 40(2):237–249

    Article  Google Scholar 

  • Randolph MF, Wroth CP (1978) Analysis of deformation of vertically loaded piles. J Geotech Eng Div ASCE 104(GT12):1465–1488

    Google Scholar 

  • Sanchez-Salinero I (1982) Static and dynamic stiffness of single piles, Geotech. Eng. Rep. GR82-31. Austin: University of Texas

  • Scott RF (1981) Foundation analysis. Prentice Hall, New Jersey

    Google Scholar 

  • Seed HB, Reese LC (1957) The action of soft clay along friction piles. Trans. ASCE 122

  • Thomas GE (1980) Equivalent spring and damping coefficient for piles subjected to vertical dynamic loads. MS thesis. Rensselaer Polytechnic Institute. New York

Download references

Author information

Authors and Affiliations

  1. Department of Civil Engineering, Democritus University of Thrace (DUTh), Xanthi, Greece

    E. G. Psaroudakis

  2. Thessaloniki, Greece

    E. G. Psaroudakis

  3. Chair Geotechnics and Soil-Structure Interaction, University of Bristol, Queen’s Building, University Walk, Clifton, Bristol, BS8 1TR, UK

    G. E. Mylonakis

  4. Section of Geotechnical Engineering, Department of Civil Engineering, Democritus University of Thrace (DUTh), Building B’, University Campus of Xanthi–Kimmeria, 67100, Xanthi, Greece

    N. S. Klimis

Authors
  1. E. G. Psaroudakis
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. G. E. Mylonakis
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. N. S. Klimis
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to E. G. Psaroudakis.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Psaroudakis, E.G., Mylonakis, G.E. & Klimis, N.S. Non-Linear Analysis of Axially Loaded Piles Using “t–z” and “q–z” Curves. Geotech Geol Eng 37, 2293–2302 (2019). https://doi.org/10.1007/s10706-019-00823-2

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10706-019-00823-2

Keywords

Search

Navigation