Multi-adaptive spatial discretization of bond-based peridynamics

Abstract

Peridynamic (PD) models are commonly implemented by exploiting a particle-based method referred to as standard scheme. Compared to numerical methods based on classical theories (e.g., the finite element method), PD models using the meshfree standard scheme are typically computationally more expensive mainly for two reasons. First, the nonlocal nature of PD requires advanced quadrature schemes. Second, non-uniform discretizations of the standard scheme are inaccurate and thus typically avoided. Hence, very fine uniform discretizations are applied in the whole domain even in cases where a fine resolution is per se required only in a small part of it (e.g., close to discontinuities and interfaces). In the present study, a new framework is devised to enhance the computational performance of PD models substantially. It applies the standard scheme only to localized regions where discontinuities and interfaces emerge, and a less demanding quadrature scheme to the rest of the domain. Moreover, it uses a multi-grid approach with a fine grid spacing only in critical regions. Because these regions are identified dynamically over time, our framework is referred to as multi-adaptive. The performance of the proposed approach is examined by means of two real-world problems, the Kalthoff–Winkler experiment and the bio-degradation of a magnesium-based bone implant screw. It is demonstrated that our novel framework can vastly reduce the computational cost (for given accuracy requirements) compared to a simple application of the standard scheme.

1 Introduction

Material failure and fracture modeling represents a major issue for researchers and practitioners in computational mechanics (Ravi-Chandar 2004; Anderson 2017). During the past years, several approaches based on classical continuum mechanics (CCM) have been employed to this end. However, their application introduces some difficulties related to the presence of spatial derivatives of displacements in the governing equations, which are undefined wherever continuity of displacement fields is not verified (Silling 2000; Bobaru et al. 2016). Many scientists have therefore tried to equip these methods with the capability to simulate crack formation and propagation (Kuhn and Müller 2008; Amor et al. 2009; Moës et al. 1999; Belytschko and Black 1999; Ortiz et al. 1987; Pepe et al. 2020; Reccia et al. 2018), but all the proposed strategies present some drawbacks (Bobaru et al. 2016).

In recent years, innovative approaches based on the peridynamic (PD) theory (Silling 2000; Silling et al. 2007), a nonlocal reformulation of classical continuum mechanics based on integro-differential equations, have been proposed to address the shortcomings of CCM-based methods in respect of the treatment of discontinuities.

The PD theory deals with integral equations rather than spatial differentiation. Therefore, the PD governing equations are valid even in presence of discontinuous displacement fields, allowing complex phenomena such as nucleation, propagation, and branching of cracks to be treated as natural material responses.

The accurate computation of integrals is of great interest in the numerical implementation of PD models, since spatial integration plays a crucial role in PD.

The majority of the implementations of PD models employ the particle-based method introduced in Silling and Askari (2005), here referred to as standard discretization scheme, which is meshfree since it does not depend on any element or geometrical connection between the underlying grid of nodes through which the body is discretized.

In recent years, the reduction of the computational burden of PD models has been the subject of various studies. A series of works have in fact attempted to enhance the computer implementation of PD models through high performance computing methods (Mossaiby et al. 2017; Diehl et al. 2020; Boys et al. 2021; Brothers et al. 2014; Fan and Li 2017), whereas other studies have proposed adaptive grid refinement algorithms to optimize the usage of the computational resources (Bobaru et al. 2009; Bobaru and Ha 2011; Dipasquale et al. 2014; Shojaei et al. 2018; Bazazzadeh et al. 2020; Gu et al. 2017). Another branch of studies have focused their attention on the development of approaches which couple PD-based models with methods based on CCM, most commonly the finite element method (FEM) (Oterkus et al. 2012; Han and Lubineau 2012; Lubineau et al. 2012; Yu et al. 2018; Sun and Fish 2019; Galvanetto et al. 2016; Wildman and Gazonas 2014; Shojaei et al. 2016; Zaccariotto et al. 2018; Ongaro et al. 2021, 2022, 2023; Seleson et al. 2013; D’Elia et al. 2021; Wang et al. 2019b; Seleson et al. 2015). Despite the proven efficiency of these approaches, they all suffer from some limitations (Mossaiby et al. 2022; Ongaro et al. 2021; Zaccariotto et al. 2018) which mainly arise out of the difference in dispersion relations of the coupled approaches (Shojaei et al. 2023; Hermann et al. 2023).

In Shojaei et al. (2022), to boost the numerical performance of PD models, the authors have introduced an efficient meshfree-collocation scheme to discretize the PD governing equations both in elasticity and diffusion problems. As comprehensively discussed in Shojaei et al. (2022), despite its advantages in terms of computational cost and computation of spatial integrals, the proposed collocation scheme may be affected by a loss of accuracy in the proximity of critical regions, i.e., regions characterized by the presence of discontinuities or with complex geometrical details, and close to the boundary of the body, where, instead, the standard scheme is known to perform better. Therefore, in Shojaei et al. (2022), the authors have introduced a hybrid meshfree discretization which exploits the advantages of both the standard and collocation schemes by combining them within an adaptive framework. In the hybrid configuration, the application of the standard scheme is in fact limited to localized critical regions and boundaries, while the remaining regions of the body are discretized through the more efficient collocation scheme.

In the present work, to further improve the numerical performance of PD models, the use of the hybrid discretization is integrated with the implementation of the multi-grid method presented in Shojaei et al. (2018), in which a PD model characterized by variable grid size is achieved by coupling grids with different spacings. In this way, the use of a fine grid is restricted only to the small portions of the domain in which it is required (i.e., critical regions and boundaries, since adopting a finer grid along the boundary is in fact an effective way to decrease the well-known surface effect of PD models), whereas the remaining part of the domain is discretized through a coarser grid. In the present study, critical regions and boundaries are therefore discretized using the standard scheme and a fine grid, while the collocation scheme and coarse grid are employed to discretize the remaining regions. The proposed approach is referred to as multi-adaptive, since, inspired by Shojaei et al. (2016), an adaptive algorithm is designed to dynamically switch both the discretization scheme and the grid spacing of the regions represented by the collocation scheme and discretized with a coarse grid to the standard scheme and fine grid spacing. Thanks to this algorithm, the parts discretized using the standard scheme and a fine grid evolve in time and track the evolution of the critical regions (e.g., the emerging crack morphology in dynamic fracture problems), while updating the coupling configuration accordingly.

This results in a highly performing and efficient pure PD model which optimally exploits the computational resources.

The capabilities of the proposed approach are assessed by performing some numerical examples, including brittle fracture and corrosion problems in two and three dimensions. The high performance of the developed framework is highlighted by the comparison of the obtained solutions with those generated by PD models represented by the standard scheme and which respectively employ a uniform coarse discretization, a uniform fine discretization, and a non-uniform discretization based on the aforementioned multi-grid approach (Shojaei et al. 2018).

The present work is an extension of the hybrid scheme by Shojaei et al. (2022) to non-uniform discretization in space. Differently from the approach presented in Shojaei et al. (2022), this work is more focused on demonstrating the feasibility of the application of the proposed strategy to the study of large and complex structures for which a large horizon size is required and which are affected by the presence of discontinuities and interfaces in some localized regions of the domain, for which a finer resolution is required. Another innovative aspect lies in the application of the approach to a real-world bio-degradation example with physical parameters.

The contents of this paper are organized as follows. In Sect. 2, a brief overview of the bond-based version of the PD formulation for brittle fracture and diffusion problems is provided. In Sect. 3, a short summary of the standard scheme and of the collocation scheme introduced in Shojaei et al. (2022) and employed in this study is presented. In the last part of the section, the implementation of the multi-adaptive scheme is outlined, focusing on the description of the multi-grid approach presented in Shojaei et al. (2018) and of the switching strategy introduced in Shojaei et al. (2016) and exploited in the present work. In Sect. 4, the performance of the proposed multi-adaptive scheme is numerically investigated with examples involving dynamic brittle fracture in two-dimensional models in Sect. 4.1, and a three-dimensional corrosion problem in Sect. 4.2. Section 5 presents some concluding remarks.

2 Overview of bond-based peridynamics

Fig. 1

Representation of a generic PD domain $\Omega$ before and after deformation; the relative position vectors (initial and current) and the relative displacement vector between the two material points $\textbf{x}$ and $\textbf{x}^\prime$ are also reported

2.1 Bond-based peridynamics for brittle fracture modeling

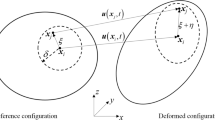
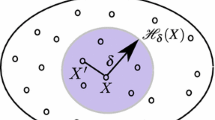
In a domain $\Omega \subset {\mathbb {R}}^p$ with p the spatial dimension, described with a PD model, each material point $\textbf{x}\in \Omega$ interacts with all the other material points located within a finite neighborhood, ${\mathcal {H}}_\textbf{x}$, of that material point (see Fig. 1). The bond-based PD equation of motion for any material point $\textbf{x}\in \Omega$ at time $t\geqslant 0$ is given by Silling (2000):

$$\begin{aligned} \rho ({\textbf{x}})\ddot{{\textbf{u}}}({\textbf{x}},t)= & {} \int _{{\mathcal {H}}_{{\textbf{x}}}}{\textbf{f}}\left( {\textbf{u}}({\textbf{x}}',t)-{\textbf{u}}({\textbf{x}},t),{\textbf{x}}'-{\textbf{x}}\right) \textrm{d}V_{{\textbf{x}}'}\nonumber \\{} & {} +{\textbf{b}}({\textbf{x}},t), \end{aligned}$$

(1)

where $\rho$ is the mass density, $\ddot{\textbf{u}}$ is the second derivative in time of the displacement field $\textbf{u}$, $\textbf{f}$ denotes the pairwise force function, which represents the force per unit volume squared (or the micro-force density) that the material point $\textbf{x}^\prime$ exerts on the material point $\textbf{x}$, and $\textbf{b}$ is a prescribed body force density field. The neighborhood ${{\mathcal {H}}_\textbf{x}}$ is defined by:

$$\begin{aligned} {\mathcal {H}}_{{\textbf{x}}}:=\left\{ {\textbf{x}}'\in \Omega :\Vert {\textbf{x}}'-{\textbf{x}}\Vert \le \delta \right\} , \end{aligned}$$

(2)

where $\delta >0$ is the horizon. For material points in the bulk of the body, i.e., material points $\textbf{x}\in \Omega$ further than $\delta$ from the boundary of the body, $\partial \Omega$, the neighborhood ${\mathcal {H}}_{{\textbf{x}}}$ represents a line segment in one dimension, a disc in two dimensions, and a ball in three dimensions centered at $\textbf{x}$.

The relative position vector of the two material points $\textbf{x}$ and $\textbf{x}^\prime$ in the reference configuration (or initial relative position vector) is denoted by (see Fig. 1):

$$\begin{aligned} \varvec{\xi }:={\textbf{x}}'-{\textbf{x}}, \end{aligned}$$

(3)

which represents the standard peridynamic notation for a bond.

In the deformed configuration at time $t>0$, the two material points $\textbf{x}$ and $\textbf{x}^\prime$ would be displaced, respectively, by $\textbf{u}(\textbf{x}, t)$ and $\textbf{u}(\textbf{x}^\prime , t)$. As depicted in Fig. 1, the corresponding relative displacement vector is defined as ${\varvec{\eta }} :=\textbf{u}(\textbf{x}',t)-\textbf{u}(\textbf{x},t)$.

The force vector $\textbf{f}$, also called bond force, acts in the direction of the line connecting the two material points $\textbf{x}$ and $\textbf{x}^\prime$, i.e., in the direction of their relative position vector in the deformed configuration $(\varvec{\eta } + \varvec{\xi }),$ usually referred to as current relative position vector (see Fig. 1).

The general form of the pairwise force function ${\textbf{f}}$, which contains all the constitutive information of the material, can be written as:

$$\begin{aligned} {\textbf{f}}(\varvec{\eta } \varvec{\xi })=f(\varvec{\eta } \varvec{\xi })\frac{\varvec{\eta }+\varvec{\xi }}{\Vert \varvec{\eta }+\varvec{\xi }\Vert }, \end{aligned}$$

(4)

where $f(\varvec{\eta },\varvec{\xi })$ is a scalar-valued even function which is defined based on the material type.

In the case of the prototype microelastic brittle (PMB) material model introduced in Silling and Askari (2005), $f(\varvec{\eta },\varvec{\xi })$ is given by:

$$\begin{aligned} f(\varvec{\eta },\varvec{\xi })=cs, \end{aligned}$$

(5)

where c is referred to as micromodulus function and represents the bond elastic stiffness, and s is the bond stretch which is expressed by:

$$\begin{aligned} s=\frac{\Vert \varvec{\eta }+\varvec{\xi } \Vert -\Vert \varvec{\xi } \Vert }{\Vert \varvec{\xi }\Vert }.\end{aligned}$$

(6)

In the case of small deformations, in view of (5) and assuming $\Vert \varvec{\eta }\Vert \ll \delta$, the linearized version of (4) can be written as:

$$\begin{aligned} \textbf{f}(\varvec{\eta },\varvec{\xi }) =c\frac{\varvec{\xi } \otimes \varvec{\xi }}{\Vert \varvec{\xi } \Vert ^{3}}\varvec{\eta }. \end{aligned}$$

(7)

It is possible to relate the micromodulus function c to measurable macroscopic quantities such as the tensile modulus E and the Poisson’s ratio $\nu$ of the material.

It is necessary to emphasize that, as a consequence of the bond-based PD formulation, in which the bonds are characterized based only on pairwise interactions, the Poisson’s ratio is restricted to a fixed value. For three-dimensional and two-dimensional plane strain cases, the Poisson’s ratio is fixed to $\nu = 1/4$, whereas for the two-dimensional plane stress case it is restricted to $\nu = 1/3$ (Silling 2000; Gerstle et al. 2005). This limitation has been eliminated in the state-based version of the theory introduced in Silling et al. (2007). The procedure adopted to obtain the bond elastic stiffness in terms of the aforementioned macroscopic quantities is comprehensively outlined in Silling and Askari (2005), Gerstle et al. (2005), Bobaru et al. (2009), Ha and Bobaru (2010). In the present work, a constant micromodulus function is employed.

In the PMB material model, failure can be introduced by establishing a predefined limit value for the bond stretch $s_{0}$, usually referred to as critical stretch, and considering a bond to be broken when its current stretch exceeds this limit value (Silling and Askari 2005). The adopted failure criterion is therefore referred to as maximum stretch criterion.

For this material model, (4) can be rewritten as (Silling 2000):

$$\begin{aligned} \textbf{f}(\varvec{\eta },\varvec{\xi })=\mu (\varvec{\xi },t)cs\frac{\varvec{\eta }+\varvec{\xi }}{\Vert \varvec{\eta }+\varvec{\xi } \Vert }, \end{aligned}$$

(8)

where $\mu (\varvec{\xi },t)$ is a history-dependent scalar-valued function which is introduced as a bond-breaking parameter, and can therefore assume either of the following two values:

$$\begin{aligned} \mu (\varvec{\xi },t) =\left\{ \begin{array}{cc} 1 \quad &{} \text {if}\text { } \text { }\text { } s(t')<s_ {0},\text { }0<t'<t, \\ \ 0 \quad &{} \text {otherwise}.\end{array}\right. \end{aligned}$$

(9)

The critical stretch $s_{0}$ can be related to measurable macroscopic quantities such as the critical energy release rate of the material $G_{0}$ (see Silling and Askari (2005)).

The interested reader may refer to Dipasquale et al. (2022) for determining the critical stretch in state-based PD. The history-dependence of the constitutive model is a consequence of the fact that the rupture of a bond is an irreversible process.

The concept of damage at a material point $\textbf{x}$ at time t is then expressed by introducing a local damage index, $\varphi ({\textbf{x}},t)$, which is defined by the following relation:

$$\begin{aligned} \varphi (\textbf{x},t)=1- \frac{\int _{\mathcal {H}_ {\textbf{x}}}\mu (\varvec{\xi },t)\textrm{d}V_{\textbf{x}'}}{\int _{\mathcal {H}_ {\textbf{x}}}\textrm{d}V_{\textbf{x}'}}, \end{aligned}$$

(10)

where $0 \le \varphi ({\textbf{x}},t) \le 1$, 0 represents the undamaged state of the material, and 1 indicates the complete disconnection of the material point $\textbf{x}$ from all the material points located within its neighborhood (Silling and Askari 2005).

The nonlocal nature of peridynamics introduces an important issue regarding the application of boundary conditions. Considering that the PD equilibrium equations are based on integral operators instead of partial differential operators, their variational nature does not result in natural (Neumann) boundary conditions, as is the case of classical continuum mechanics models (Macek and Silling 2007). As a consequence, in a domain described with a PD model, the prescribed displacements or loads need to be applied through a finite volume of boundary layers, rather than on a surface. The depth of the boundary layer along the material boundary is usually set to be equal to $\delta$, as suggested by the numerical investigations carried out in Macek and Silling (2007).

2.2 Peridynamic diffusion formulation

In the following section, a brief outline of the nonlocal formulation of bond-based PD for diffusion-type problems is provided. A comprehensive derivation of the formulation is presented in Bobaru and Duangpanya (2010, 2012). The model is constructed by associating a concentration value $C({\textbf{x}},t)$ to each material point $\textbf{x}\in \Omega$ at time t. Each material point $\textbf{x}$ is connected with all the material points $\textbf{x}'$ located within a finite neighborhood, ${\mathcal {H}}_\textbf{x}$, through pipe-like conductors which are usually referred to as diffusion bonds. In this framework, each bond $\varvec{\xi }:=\textbf{x}'-\textbf{x}$ can be thought of as a pipe which transfers the concentration between two buckets, i.e., the two material points $\textbf{x}$ and $\textbf{x}'$ at its ends. In the bond-based PD diffusion formulation, which is the version of PD that is employed in this work, the transport of the concentration in each bond $\varvec{\xi }$ is independent of the transport in the other bonds (Bobaru and Duangpanya 2012).

The bond-based PD governing equation of diffusion for any material point $\textbf{x}\in \Omega$ at time $t\geqslant 0$ is given by Bobaru and Duangpanya (2010):

$$\begin{aligned} {\dot{C}}({\textbf{x}},t)= & {} \int _{{\mathcal {H}}_{{\textbf{x}}}}J\left( C({\textbf{x}}',t)-C({\textbf{x}},t),{\textbf{x}}'-{\textbf{x}}\right) \textrm{d}V_{{\textbf{x}}'}\nonumber \\{} & {} +S({\textbf{x}},t), \end{aligned}$$

(11)

where C represents the concentration field, ${\dot{C}}$ is the first time derivative of C, S is a given source function, and J is the kernel of the integral operator or the concentration flow density which takes the following form (Zhao et al. 2018):

$$\begin{aligned} J\left( \Theta ,\varvec{\xi } \right) =\left\{ \begin{array}{cc} \kappa \frac{1}{\Vert \varvec{\xi } \Vert ^{q}}\Theta \quad &{} \Vert \varvec{\xi }\Vert \le \delta , \\ \\ 0 \quad &{} \Vert \varvec{\xi }\Vert > \delta , \end{array}\right. \end{aligned}$$

(12)

where $\delta >0$ is the horizon (see Sect. 2.1), $\Theta := C({\textbf{x}}',t)-C({\textbf{x}},t)$, q is an integer that influences the shape of the kernel J and is normally selected to be equal to 0, 1, or 2 (see Chen and Bobaru (2015b) for further details), and $\kappa$ is referred to as the PD micro-diffusivity. Several forms are proposed for $\kappa$. In this work, a constant micro-diffusivity is employed (Zhao et al. 2018). The PD micro-diffusivity can be related to the diffusion coefficient ${\mathcal {K}}$ of the classical local diffusion equation by equating the PD flux to that of the local diffusion as comprehensively outlined in Bobaru and Duangpanya (2010); Shojaei et al. (2020). In two-dimensional diffusion, assuming $q = 2$, $\kappa$ can be expressed by the following relation:

$$\begin{aligned} \kappa =\frac{4{\mathcal {K}}}{\pi \delta ^2}. \end{aligned}$$

(13)

Similar to what introduced in Sect. 2.1 for the elasticity case, in PD diffusion, the boundary conditions need to be applied through a finite volume of boundary layers whose depth is typically taken equal to $\delta$. A part of the source function S in (11) contains Neumann-type boundary conditions (see Chen and Bobaru (2015b), Wang et al. (2019a)).

3 Standard and proposed discretization schemes

3.1 The standard scheme

Fig. 2

Schematic representation of the neighborhood associated to node ${\textbf{x}}_{i}$ in the standard discretization scheme

The numerical discretization of peridynamic models can be pursued by employing different numerical methods (Emmrich and Weckner 2007). The most common approach used to discretize the PD governing equation is the meshfree scheme introduced in Silling and Askari (2005), here referred to as standard discretization scheme (Shojaei et al. 2022). In this framework, the numerical approximation of the peridynamic equation requires the subdivision of the domain into a grid of points called nodes: in a domain $\Omega$, described with a PD model, each node ${\textbf{x}}_{i} \in \Omega$ is associated to a certain finite volume in the reference configuration, such that the set of nodes forms a uniform grid in which the distance between two nearest neighboring nodes is referred to as grid spacing (see Fig. 2). In the uniform grid configuration, $\Delta x = \Delta y = \Delta z$, where $\Delta x$, $\Delta y$, and $\Delta z$ are the grid spacings in the x-, y-, and z-directions, respectively. No elements or other geometrical connections between nodes are foreseen (Silling and Askari 2005). The volume associated to each node ${\textbf{x}}_{i}$, i.e., the node volume, is computed as a cube of volume $V_{i} = \Delta x^{3}$ for three-dimensional models, as a square cell of volume $V_{i} = \Delta x^{2} {\bar{t}}$ for the planar cases, and as $V_{i} = A \Delta x$ for one-dimensional systems, where ${\bar{t}}$ and A are the thickness and constant cross-sectional area of two- and one-dimensional domains, respectively. The node of interest ${\textbf{x}}_{i}$ at which the volume is centered is referred to as source node. Moreover, time is discretized into instants, i.e., $t^{0}, t^{1}, t^{2}, \ldots , t^{n-1}, t^{n}$, where n represents the time step number.

In the standard discretization scheme, the discretized form of the bond-based PD equation of motion (cf. (1)) for any source node ${\textbf{x}}_{i} \in \Omega$ at the time instant $t^{n}$ is obtained by replacing the integral in (1) by a finite sum as follows:

$$\begin{aligned} \rho _{i}\ddot{{\textbf{u}}}^{n}_{i}{=}\sum _{j\in {\mathcal {F}}_{i}}{\textbf{f}}\left( {\textbf{u}}^{n}_{j}{-}{\textbf{u}}^{n}_{i},{\textbf{x}}_{j}{-}{\textbf{x}}_{i}\right) \beta \left( {\textbf{x}}_{j}{-}{\textbf{x}}_{i}\right) V_{j}{+}{\textbf{b}}^{n}_{i}.\nonumber \\ \end{aligned}$$

(14)

In the same way, the discretized form of the PD diffusion equation (cf. (11)) is derived by substituting the integral in (11) by a finite sum, such that:

$$\begin{aligned} {\dot{C}}^{n}_{i}{=}\sum _{j\in {\mathcal {F}}_{i}}J\left( C^{n}_{j}{-}C^{n}_{i},{\textbf{x}}_{j}{-}{\textbf{x}}_{i}\right) \beta \left( {\textbf{x}}_{j}{-}{\textbf{x}}_{i}\right) V_{j}{+}S^{n}_{i}.\nonumber \\ \end{aligned}$$

(15)

In (14) and (15), i is the index of the source node, j is the index associated to the set of family nodes ${\mathcal {F}}_{i}$, which includes all nodes within the finite neighborhood ${\mathcal {H}}_{{\textbf{x}}_{i}}$ of node ${\textbf{x}}_{i}$, $V_{j}$ is the discretized volume associated to node ${\textbf{x}}_{j}$, and $\beta \left( \varvec{\xi }\right)$ is a volume correction factor used to approximate the portion of $V_{j}$ that falls within the neighborhood of the source node ${\textbf{x}}_{i}$ (see Fig. 2). For two-dimensional cases, $\beta \left( \varvec{\xi }\right)$ takes the following form (Yu et al. 2011):

$$\begin{aligned} \beta (\mathbf {\xi }) =\left\{ \begin{array}{cc} 1 \quad &{} \Vert \varvec{\xi }\Vert \le \delta -\frac{1}{2}\Delta x, \\ \frac{\delta -\Vert \varvec{\xi } \Vert }{\Delta x}+\frac{1}{2} \quad &{} \delta - \frac{1}{2}\Delta x<\Vert \varvec{\xi } \Vert <\delta +\frac{1}{2} \Delta x,\\ 0 &{}\Vert \varvec{\xi } \Vert \ge \delta +\frac{1}{2}\Delta x. \end{array} \right. \nonumber \\ \end{aligned}$$

(16)

The spatial integration is performed by adopting the one-point Gauss quadrature rule. In the present work, the algorithm proposed by Yu et al. (2011) has been selected among the currently available approaches developed to improve the accuracy of the spatial integration, since it is the most commonly used among the PD community, due to its ease of implementation and quite accurate results. The quadrature algorithm proposed by Seleson (2014) and the innovative algorithm introduced in Scabbia et al. (2022) could certainly be used alternatively, perhaps leading to slightly more accurate results. However, given that the focus of the work is more on efficiency rather than on accuracy of the computations, the selected algorithm provides sufficiently accurate solutions for the type of problems considered.

A fundamental parameter of the discretized version of PD is the ratio between the horizon and the grid spacing, i.e., $m = \delta /\Delta x$; $\delta$ and m are, therefore, the two parameters which determine the number of interactions to be considered for each node in a discretized PD model.

In the present work, the time integration of the elasticity problem is performed by exploiting the velocity-Verlet time integration (Swope et al. 1982). This explicit algorithm is commonly used in the PD framework due to its robustness and numerical stability.

The time integration of the diffusion problem is instead performed by applying the explicit forward Euler algorithm. Given the nodal values of ${\textbf{x}}_{i} \in \Omega$ at time instant $t^{n}$, i.e., $C^{n}_{i}$ and ${\dot{C}}^{n}_{i}$, the update procedure for the concentration field is achieved:

$$\begin{aligned} C^{n+1}_{i}=C^{n}_{i}+\Delta t {\dot{C}}^{n}_{i}. \end{aligned}$$

(17)

For numerical stability reasons, the time step $\Delta t$ adopted during the simulations must be smaller than a predefined critical time step, $\Delta t_{\textrm{crit}}$. The computation of this critical step size has been the subject of many studies reported in literature, such as (Silling and Askari 2005; Bobaru et al. 2016; Littlewood 2015). In Silling and Askari (2005), the authors evaluated the critical time step as follows:

$$\begin{aligned} \Delta t_{\textrm{crit}} = \sqrt{\frac{2\rho }{c\sum _{j\in {\mathcal {F}}_{i}}V_{j}}}, \end{aligned}$$

(18)

where j iterates over all the family nodes of the source node ${\textbf{x}}_{i} \in \Omega$. This stability condition is particularly useful for bond-based PD models (Silling and Askari 2005).

An alternative option to compute the critical step size is to consider the well-known Courant-Friedrichs-Lewy condition, such that (Bobaru et al. 2016; Littlewood 2015):

$$\begin{aligned} \Delta t_{\textrm{crit}} = \frac{\Delta x_{\textrm{min}}}{c_{k}}, \end{aligned}$$

(19)

where $\Delta x_{\textrm{min}}$ is the smallest grid size of the discretized domain, while $c_{k}$ represents the speed of the longitudinal waves in the material, and is expressed by the following relation:

$$\begin{aligned} c_{k}=\sqrt{\frac{K}{\rho }}, \end{aligned}$$

(20)

where K is the bulk modulus of the material.

Nevertheless, the latter condition is rather conservative for PD models (Bobaru et al. 2016); in the present work, the stability condition derived in Silling and Askari (2005) is therefore considered to perform the critical time step computation.

The standard discretization scheme is easy-to-implement and can conveniently calculate the required integral terms in regions described by a nonlinear PD model including material separation (such as cracks).

However, it might become computationally expensive as soon as $\delta$ takes a large value; the issue exacerbates in three-dimensional problems where both a large horizon size and a fine grid spacing are required, such as in correspondence of the crack tip region or in the vicinity of corrosion interfaces.

This lies in the fact that, in the standard scheme, all the neighboring nodes play the role of quadrature points of integration. In Shojaei et al. (2022), to boost the numerical performance of PD solvers, it is suggested to restrict the application of the standard scheme and thus to employ an efficient meshfree-collocation scheme for regions where the application of the standard one is not necessarily required. The collocation scheme is described in the following section.

3.2 The collocation scheme

Fig. 3

Schematic representation of the neighborhood associated to node ${\textbf{x}}_{i}$ with (left) the family nodes with their corresponding integration cells in the standard scheme, (center) the family nodes surrounded by a Cartesian auxiliary grid, and (right) the selected collocation nodes in the collocation scheme

The collocation scheme is truly meshfree as it calculates the integrals semi-analytically and does not require the back ground cells of integration as in the standard scheme. In this scheme, prior to the integration, at each neighborhood ${\mathcal {H}}_{{\textbf{x}}_{i}}$, the main field variables are approximated in terms of the nodal values of a set of nodes, called collocation nodes and denoted by ${\mathcal {C}}_{i}$, that are a subset of the family nodes (i.e., ${\mathcal {C}}_{i}\subseteq {\mathcal {F}}_{i}$). Figure 3 (left) illustrates a generic PD neighborhood discretized by the standard scheme. Inspired by Shojaei et al. (2022), an auxiliary grid of nodes, centered at the source node ${\textbf{x}}_{i}$ and with a Cartesian pattern shown in Fig. 3 (center), is considered. The auxiliary grid indicates the approximate positions of the collocation nodes (i.e., the quadrature points of integration in the collocation scheme). Likewise, to each auxiliary node, the nearest family node in ${\mathcal {F}}_{i}$ is associated and thus added to the set of collocation nodes ${\mathcal {C}}_{i}$; see Fig. 3 (right). The approximation is performed via a weighted least squares (WLS) procedure which uses monomials as the basis functions. According to Shojaei et al. (2022), the number of collocation nodes $n_{c}$ depends on the order of approximation. To make the calculations efficient, the least possible bases are taken; for instance, in three dimensions:

$$\begin{aligned} {\textbf{p}}({\textbf{x}})=\left( 1,x,y,z,x^2,xy,xz,y^2,yz,z^2\right) , \end{aligned}$$

(21)

where ${\textbf{p}}({\textbf{x}})$ is a vector containing $n_{p}$ monomial basis functions, and, in this case, it represents a complete set of monomials up to the second-order. Having the field variables approximated, at nodes with a full neighborhood, within which the governing equation can be described by a linear PD model (cf. (7)), the corresponding integrals can be calculated analytically in terms of the nodal values of the collocation nodes. This results in the following equation of motion at node ${\textbf{x}}_{i}$:

$$\begin{aligned} \rho _{i}\ddot{{\textbf{u}}}^{n}_{i}\approx \bar{{\textbf{L}}}\bar{{\textbf{Q}}}_{i}\bar{{\textbf{U}}}^{n}_{i}+{\textbf{b}}^{n}_{i}, \end{aligned}$$

(22)

where $\bar{\textbf{U}}^{n}_{i}=\left( \textbf{U}^{n} _{i},\textbf{V}^{n}_{i},\textbf{W}^{n}_{i} \right) ^{\textrm{T}}$ collects the displacements, along the $x-$, $y-$, and $z-$directions, at time instant $t^{n}$:

$$\begin{aligned} {\textbf{U}}^{n}_i= & {} \left( \begin{matrix} u^{n}_{i} \\ \vdots \\ u^{n}_{j} \\ \vdots \end{matrix} \right) , \quad {\textbf{V}}^{n}_i=\left( \begin{matrix} v^{n}_{i} \\ \vdots \\ v^{n}_{j} \\ \vdots \end{matrix} \right) ,\nonumber \\ {\textbf{W}}^{n}_i= & {} \left( \begin{matrix} w^{n}_{i} \\ \vdots \\ w^{n}_{j} \\ \vdots \end{matrix} \right) ,\quad \forall \textbf{x}_j\in {\mathcal {C}}_{i}. \end{aligned}$$

(23)

In (22), the term $\bar{{\textbf{L}}}\bar{{\textbf{Q}}}_{i}$ gives rise to the weights of quadrature; $\bar{{\textbf{L}}}$ is a matrix as (Shojaei et al. 2022):

$$\begin{aligned} \bar{{\textbf{L}}}=\left[ \begin{matrix} {\textbf{L}}_{u}&{} {\textbf{L}}_{v}&{}{\textbf{L}}_{w}\\ \end{matrix}\right] , \end{aligned}$$

(24)

where:

$$\begin{aligned} \begin{aligned} {\textbf{L}}_{u}{=}&\frac{ \pi c \delta ^4}{5}\left[ \begin{array}{cccccccccc} 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 1 &{}\quad 0 &{}\quad 0 &{}\quad \frac{1}{3} &{}\quad 0 &{}\quad \frac{1}{3} \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad \frac{1}{3} &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad \frac{1}{3} &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ \end{array} \right] , \\ {\textbf{L}}_{v}{=}&\frac{ \pi c \delta ^4}{5} \left[ \begin{array}{cccccccccc} 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad \frac{1}{3} &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad \frac{1}{3} &{}\quad 0 &{}\quad 0 &{}\quad 1 &{}\quad 0 &{}\quad \frac{1}{3} \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad \frac{1}{3} &{}\quad 0 \\ \end{array} \right] ,\\ {\textbf{L}}_{w}{=}&\frac{ \pi c \delta ^4}{5}\left[ \begin{array}{cccccccccc} 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad \frac{1}{3} &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad \frac{1}{3} &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad \frac{1}{3} &{}\quad 0 &{}\quad 0 &{}\quad \frac{1}{3} &{}\quad 0 &{}\quad 1 \\ \end{array} \right] , \end{aligned}\nonumber \\ \end{aligned}$$

(25)

and $\bar{{\textbf{Q}}}_{i}$ is a matrix as:

$$\begin{aligned} \bar{{\textbf{Q}}}_{i}=\left[ \begin{matrix} {\textbf{Q}}_{i}&{}{\textbf{0}}&{}{\textbf{0}} \\ {\textbf{0}}&{}{\textbf{Q}}_{i}&{}{\textbf{0}}\\ {\textbf{0}}&{}{\textbf{0}}&{}{\textbf{Q}}_{i} \end{matrix}\right] , \end{aligned}$$

(26)

where ${\textbf{Q}}_{i}$ is obtained by:

$$\begin{aligned} {\textbf{Q}}_{i}={\textbf{A}}_{i}^{-1}{\textbf{B}}_{i}, \end{aligned}$$

(27)

in which ${\textbf{A}}_{i}$ and ${\textbf{B}}_{i}$ are two matrices required to obtain the moment matrix in the WLS approximation as (Shojaei et al. 2017, 2016):

$$\begin{aligned} {\textbf{A}}_{i}{=}\sum _{j\in {\mathcal {C}}_{i}}{\bar{\omega }}\left( {\textbf{x}}_{j}{-}{\textbf{x}}_{i}\right) {\textbf{p}}^{{\textrm{T}}}\left( {\textbf{x}}_{i}{-}{\textbf{x}}_{j}\right) {\textbf{p}}\left( {\textbf{x}}_{i}{-}{\textbf{x}}_{j}\right) , \end{aligned}$$

(28)

and:

$$\begin{aligned}{} & {} {\textbf{B}}_{i}{=} \left[ \begin{matrix}{\bar{\omega }}\left( {\textbf{x}}_{i}{-}{\textbf{x}}_{i}\right) {\textbf{p}}^{{\textrm{T}}}\left( {\textbf{x}}_{i}{-}{\textbf{x}}_{i}\right)&\cdots&{\bar{\omega }}\left( {\textbf{x}}_{j}{-}{\textbf{x}}_{i}\right) {\textbf{p}}^{\top }\left( {\textbf{x}}_{j}{-}{\textbf{x}}_{i}\right)&\cdots&\end{matrix}\right] , \nonumber \\{} & {} j\in {\mathcal {C}}_{i}. \end{aligned}$$

(29)

In (28) and (29), ${\bar{\omega }}$ is a weight function that influences the contribution of each collocation node with respect to its distance from the source node, and is taken here as (Shojaei et al. 2017; Mossaiby et al. 2020; Shojaei et al. 2016):

$$\begin{aligned} {\bar{\omega }}({\textbf{x}}-{\textbf{x}}_{i})=\frac{1-\exp \left( 64-16\frac{\Vert {\textbf{x}}-{\textbf{x}}_{i}\Vert ^{2}}{{\bar{r}}^{2}}\right) }{1-\exp (64)}, \end{aligned}$$

(30)

where ${\bar{r}}$ indicates the largest possible distance of a collocation node from the source node. A similar strategy can be employed for the discretization of the diffusion equation in (11), which leads to the following equation for the approximation within ${\mathcal {H}}_{{\textbf{x}}_{i}}$:

$$\begin{aligned} {\dot{C}}^{n}_{i}\approx {\textbf{L}}_{C}{\textbf{Q}}_{i}{\textbf{C}}^{n}_{i}+S^{n}_{i}, \end{aligned}$$

(31)

where ${\textbf{C}}_{i}^{n}$ collects the concentration values of the collocation nodes at time instant $t^{n}$:

$$\begin{aligned} {\textbf{C}}^{n}_i=\left( \begin{matrix} C^{n}_{i} \\ \vdots \\ C^{n}_{j} \\ \vdots \end{matrix} \right) , \quad \forall {\textbf{x}}_j\in {\mathcal {C}}_{i}, \end{aligned}$$

(32)

and ${\textbf{L}}_{C}$ denotes a vector obtained as follows:

$$\begin{aligned} {\textbf{L}}_{C}= \frac{4 \pi \kappa \delta ^{5-q}}{-3q+15}\left( \begin{array}{cccccccccc} 0 &{} 0 &{} 0 &{} 0 &{} 1 &{} 0 &{} 0 &{} 1 &{} 0 &{} 1 \\ \end{array} \right) . \end{aligned}$$

(33)

Therefore, the collocation scheme does not require any calculation of partial volumes and performs the integration over fewer nodes compared with the standard scheme. The reader may refer to Shojaei et al. (2022) to get an insight into the convergence and accuracy of the collocation scheme.

3.3 The multi-adaptive scheme

As mentioned in Sect. 1, the use of the hybrid discretization introduced in Shojaei et al. (2022) is here integrated with the implementation of the multi-grid method developed in Shojaei et al. (2018) with the aim of maximizing the numerical performance of PD models. In the following sections, the implementation of the resulting framework, referred to as multi-adaptive scheme, is therefore outlined, with a focus on the description of the multi-grid approach developed to couple grids with different grid size (Shojaei et al. 2018) and of the switching strategy implemented to adaptively track the evolution of the critical regions (Shojaei et al. 2016).

3.3.1 Coupling grids with different grid size

Fig. 4

Schematic representation of fictitious material points in the proximity of a critical region and computation of the corresponding data from the counterpart active domain

Fig. 5

Schematic representation of the domain; (left) fine grid, (right) coarse grid. For clarity reasons, $m^{-} = \delta /\Delta x^{-}= 2$ is adopted in the fine region of the domain, whereas $m^{+} = \delta /\Delta x^{+}= 1$ is considered in the coarse portion of the domain, where $\delta$ is the horizon. Note that here $\Delta x^{+}=2\Delta x^{-}$ only as an example

The multi-adaptive scheme can be presented by considering a generic PD domain $\Omega$ containing one or more discontinuities, which may propagate, branch, or coalesce due to a deformation process. In the proposed framework, boundaries and critical regions surrounding the discontinuities are discretized using the standard scheme and a fine grid, whereas the remaining part of the domain is discretized through the collocation scheme and a coarser grid (see Sect. 1).

Coarse and fine portions of the domain, which are respectively referred to as $\Omega ^{+}$ and $\Omega ^{-}$, need to be coupled to ensure that the material points near the borders of critical regions and boundaries have a complete neighborhood.

The idea behind the multi-grid approach introduced in Shojaei et al. (2018) is to consider a series of fictitious material points, both in the $\Omega ^{+}$ and $\Omega ^{-}$ portions, where the material points near the borders of the critical regions and the boundaries expect for a complete neighborhood.

It is important to highlight that the fictitious material points serve the function of completing the neighborhood of other material points, thus making the coarse and fine grids independent.

As depicted in Fig. 4, the independence of the grids is achieved by considering two similar but distinct domains, one for the PD model discretized through the standard scheme and the fine grid, and the other for the PD model represented by the collocation scheme and discretized with the coarse grid.

With reference to Fig. 4, ${\textbf{x}}$ is a material point belonging to the domain $\Omega ^{-}$, i.e., to the domain discretized with a fine grid spacing, while ${\textbf{x}}'$ is a fictitious material point in the fine grid which corresponds to a missing neighbor for ${\textbf{x}}$.

The interaction between ${\textbf{x}}$ and ${\textbf{x}}'$ is established following the calculation of the quantities (e.g., displacement, velocity, acceleration) associated with ${\textbf{x}}'$. Given that these data are only available in the domain $\Omega ^{+}$ (see Fig. 4), they are computed by interpolating the values of the required quantities at the material points adjacent to ${\textbf{x}}'$ in $\Omega ^{+}$. The quantities associated to the fictitious material points in the coarse grid are likewise computed by interpolating the values of the corresponding quantities at the adjacent material points in $\Omega ^{-}$.

This results in the domains being constrained to each other, since the solution of the portion of $\Omega ^{-}$ outside the critical region in Fig. 4 is bound to its corresponding region in $\Omega ^{+}$, while the solution in correspondence of the critical region in $\Omega ^{+}$ is constrained to its counterpart in $\Omega ^{-}$.

As shown in Fig. 4, the domains are characterized by active and inactive regions, where the inactive regions represent the constrained parts of the solution which are no longer needed, and thus not taken into account in the computation. The advantages of such a configuration are represented by the possibility of conserving the total mass of the system and of discretizing each domain independently and in advance, such that to increase the efficiency of the adaptive refinement procedure implemented to follow the evolution of the critical regions. The discretized form of the multi-grid scheme can be easily introduced by considering the same portion of the domain $\Omega$ in proximity of the border of the critical region depicted in Fig. 4 in both the $\Omega ^{-}$ and $\Omega ^{+}$ domains, as schematically represented in Fig. 5. In the following, $\Delta x^{-}$ and $\Delta x^{+}$ represent the grid spacings employed to discretize the $\Omega ^{-}$ and $\Omega ^{+}$ domains, respectively. Four different types of nodes are identified within the discretized domains, i.e., active and fictitious nodes in the fine grid and active and fictitious nodes in the coarse grid. As depicted in Fig. 5, the neighbors of an active node ‘$\textrm{a}$’ in the fine grid are composed of both active and fictitious nodes, respectively represented by ‘$\textrm{a}_{j}$’ and ‘$\textrm{a}_{k}$’. Similarly, the neighbors of an active node ‘$\textrm{B}$’ in the coarse grid are composed of both active and fictitious nodes, respectively marked as ‘$\textrm{B}_{j}$’ and ‘$\textrm{B}_{k}$’.

In the following, the time marching scheme for a general active node ‘$\textrm{a}$’ in the fine grid is outlined in the elasticity problem, such that:

$$\begin{aligned} {\textbf{u}}^{n+1}_{\textrm{a}}&= {\textbf{u}}^{n}_{\textrm{a}} + \Delta t \dot{{\textbf{u}}}^{n}_{\textrm{a}} + \frac{\Delta t^{2}}{2} \ddot{{\textbf{u}}}^{n}_{\textrm{a}}, \end{aligned}$$

(34a)

$$\begin{aligned} \ddot{{\textbf{u}}}^{n+1}_{\textrm{a}}&= \frac{1}{\rho } \Bigl [ {\textbf{f}}\left( {\textbf{u}}^{n+1}_{\textrm{a}_{j}} - {\textbf{u}}^{n+1}_{\textrm{a}}, {\textbf{x}}_{\textrm{a}_{j}} - {\textbf{x}}_{\textrm{a}}\right) \nonumber \\&\quad \beta \left( {\textbf{x}}_{\textrm{a}_{j}} - {\textbf{x}}_{\textrm{a}}\right) V_{\textrm{a}_{j}}+ \cdots \nonumber \\&\quad + {\textbf{f}}\left( {\textbf{u}}^{n+1}_{\textrm{a}_{k}} - {\textbf{u}}^{n+1}_{\textrm{a}}, {\textbf{x}}_{\textrm{a}_{k}} - {\textbf{x}}_{\textrm{a}}\right) \nonumber \\&\quad \beta \left( {\textbf{x}}_{\textrm{a}_{k}} - {\textbf{x}}_{\textrm{a}}\right) V_{\textrm{a}_{k}} + \cdots +{\textbf{b}}^{n+1}_{\textrm{a}}\Bigr ], \end{aligned}$$

(34b)

$$\begin{aligned} \dot{{\textbf{u}}}^{n+1}_{\textrm{a}}&= \dot{{\textbf{u}}}^{n}_{\textrm{a}} +\frac{\Delta t}{2}\left( \ddot{{\textbf{u}}}^{n}_{\textrm{a}} + \ddot{{\textbf{u}}}^{n+1}_{\textrm{a}}\right) , \end{aligned}$$

(34c)

and in the diffusion problem, such that:

$$\begin{aligned} C^{n+1}_{\textrm{a}}&= C^{n}_{\textrm{a}} + \Delta t {\dot{C}}^{n}_{\textrm{a}}, \end{aligned}$$

(35a)

$$\begin{aligned} {\dot{C}}^{n+1}_{\textrm{a}}&= J\left( C^{n+1}_{\textrm{a}_{j}} - C^{n+1}_{\textrm{a}}, {\textbf{x}}_{\textrm{a}_{j}} - {\textbf{x}}_{\textrm{a}}\right) \nonumber \\&\quad \beta \left( {\textbf{x}}_{\textrm{a}_{j}} - {\textbf{x}}_{\textrm{a}}\right) V_{\textrm{a}_{j}}+ \cdots \nonumber \\&\quad + J\left( C^{n+1}_{\textrm{a}_{k}} - C^{n+1}_{\textrm{a}}, {\textbf{x}}_{\textrm{a}_{k}} - {\textbf{x}}_{\textrm{a}}\right) \nonumber \\&\quad \beta \left( {\textbf{x}}_{\textrm{a}_{k}} - {\textbf{x}}_{\textrm{a}}\right) V_{\textrm{a}_{k}} + \cdots +S^{n+1}_{\textrm{a}}. \end{aligned}$$

(35b)

In (34b) and (35b), the dots on the right-hand side indicate the contribution of other active and fictitious nodes in the neighborhood of the active node ‘$\textrm{a}$’, similar to the ones already provided for ‘$\textrm{a}_{j}$’ and ‘$\textrm{a}_{k}$’.

Likewise, the time marching scheme for a general active node ‘$\textrm{B}$’ in the coarse grid is defined in the elasticity problem, such that:

$$\begin{aligned} {\textbf{u}}^{n+1}_{\textrm{B}}&= {\textbf{u}}^{n}_{\textrm{B}} + \Delta t \dot{{\textbf{u}}}^{n}_{\textrm{B}} + \frac{\Delta t^{2}}{2} \ddot{{\textbf{u}}}^{n}_{\textrm{B}}, \end{aligned}$$

(36a)

$$\begin{aligned} \ddot{{\textbf{u}}}^{n+1}_{\textrm{B}}&= \frac{1}{\rho } \Bigl [ {\textbf{f}}\left( {\textbf{u}}^{n+1}_{\textrm{B}_{j}} - {\textbf{u}}^{n+1}_{\textrm{B}}, {\textbf{x}}_{\textrm{B}_{j}} - {\textbf{x}}_{\textrm{B}}\right) \nonumber \\&\quad \beta \left( {\textbf{x}}_{\textrm{B}_{j}} - {\textbf{x}}_{\textrm{B}}\right) V_{\textrm{B}_{j}} + \cdots \nonumber \\&\qquad + {\textbf{f}}\left( {\textbf{u}}^{n+1}_{\textrm{B}_{k}} - {\textbf{u}}^{n+1}_{\textrm{B}}, {\textbf{x}}_{\textrm{B}_{k}} - {\textbf{x}}_{\textrm{B}}\right) \nonumber \\&\quad \beta \left( {\textbf{x}}_{\textrm{B}_{k}} - {\textbf{x}}_{\textrm{B}}\right) V_{\textrm{B}_{k}} + \cdots +{\textbf{b}}^{n+1}_{\textrm{B}}\Bigr ], \end{aligned}$$

(36b)

$$\begin{aligned} \dot{{\textbf{u}}}^{n+1}_{\textrm{B}}&= \dot{{\textbf{u}}}^{n}_{\textrm{B}} +\frac{\Delta t}{2}\left( \ddot{{\textbf{u}}}^{n}_{\textrm{B}} + \ddot{{\textbf{u}}}^{n+1}_{\textrm{B}}\right) , \end{aligned}$$

(36c)

and in the diffusion problem, such that:

$$\begin{aligned} C^{n+1}_{\textrm{B}}&= C^{n}_{\textrm{B}} + \Delta t {\dot{C}}^{n}_{\textrm{B}}, \end{aligned}$$

(37a)

$$\begin{aligned} {\dot{C}}^{n+1}_{\textrm{B}}&= J\left( C^{n+1}_{\textrm{B}_{j}} - C^{n+1}_{\textrm{B}}, {\textbf{x}}_{\textrm{B}_{j}} - {\textbf{x}}_{\textrm{B}}\right) \nonumber \\&\quad \beta \left( {\textbf{x}}_{\textrm{B}_{j}} - {\textbf{x}}_{\textrm{B}}\right) V_{\textrm{B}_{j}} + \cdots \nonumber \\&\quad + J\left( C^{n+1}_{\textrm{B}_{k}} - C^{n+1}_{\textrm{B}}, {\textbf{x}}_{\textrm{B}_{k}} - {\textbf{x}}_{\textrm{B}}\right) \nonumber \\&\quad \beta \left( {\textbf{x}}_{\textrm{B}_{k}} - {\textbf{x}}_{\textrm{B}}\right) V_{\textrm{B}_{k}} + \cdots +S^{n+1}_{\textrm{B}}. \end{aligned}$$

(37b)

In (36b) and (37b), the dots on the right-hand side indicate the contribution of other active and fictitious nodes in the neighborhood of the active node ‘$\textrm{B}$’, similar to the ones already provided for ‘$\textrm{B}_{j}$’ and ‘$\textrm{B}_{k}$’.

Following the definition of the time marching scheme, the interpolation scheme for evaluating the quantities associated with the fictitious nodes in the coarse and fine grids is then presented in both the elasticity and diffusion problems. As schematically represented in Fig. 5, ‘$\textrm{B}_{k}$’ represents a fictitious node in the coarse grid, whose associated values (e.g., displacement, velocity, and acceleration) are derived from a simple interpolation, based on inverse distance weighting, over the corresponding values of its surrounding active nodes in the fine grid ‘$\text {b}_{1}$’ to ‘$\text {b}_{4}$’, such as:

$$\begin{aligned} {\textbf{u}}^{n+1}_{\textrm{B}_{k}}&= \frac{\sum ^{4}_{j = 1}\frac{1}{\Vert {\textbf{x}}_{\textrm{B}_k} - {\textbf{x}}_{\textrm{b}_j}\Vert }{\textbf{u}}^{n+1}_{\textrm{b}_j}}{\sum ^{4}_{j = 1}\frac{1}{\Vert {\textbf{x}}_{\textrm{B}_k} - {\textbf{x}}_{\textrm{b}_j}\Vert }}, \end{aligned}$$

(38a)

$$\begin{aligned} \dot{{\textbf{u}}}^{n+1}_{\textrm{B}_{k}}&= \frac{\sum ^{4}_{j = 1}\frac{1}{\Vert {\textbf{x}}_{\textrm{B}_k} - {\textbf{x}}_{\textrm{b}_j}\Vert }\dot{{\textbf{u}}}^{n+1}_{\textrm{b}_j}}{\sum ^{4}_{j = 1}\frac{1}{\Vert {\textbf{x}}_{\textrm{B}_k} - {\textbf{x}}_{\textrm{b}_j}\Vert }}, \end{aligned}$$

(38b)

in the elasticity problem, and such as:

$$\begin{aligned} C^{n+1}_{\textrm{B}_{k}} = \frac{\sum ^{4}_{j = 1}\frac{1}{\Vert {\textbf{x}}_{\textrm{B}_k} - {\textbf{x}}_{\textrm{b}_j}\Vert }C^{n+1}_{\textrm{b}_j}}{\sum ^{4}_{j = 1}\frac{1}{\Vert {\textbf{x}}_{\textrm{B}_k} - {\textbf{x}}_{\textrm{b}_j}\Vert }}, \end{aligned}$$

(39)

in the diffusion problem.

Fig. 6

Schematic representation of the implementation of the switching strategy in correspondence of a critical region; configuration of $\Omega ^{-}$ and $\Omega ^{+}$ at (top) time instant $t^{n}$ and (bottom) time instant $t^{n+1}$

Correspondingly, as depicted in Fig. 5, ‘$\textrm{a}_{k}$’ represents a fictitious node in the fine grid, whose required values are derived from a simple interpolation, based on inverse distance weighting, over the corresponding values of its surrounding active nodes in the coarse grid ‘$\text {A}_{1}$’ to ‘$\text {A}_{4}$’, such as:

$$\begin{aligned} {\textbf{u}}^{n+1}_{\textrm{a}_{k}}&= \frac{\sum ^{4}_{j = 1}\frac{1}{\Vert {\textbf{x}}_{\textrm{a}_{k}} - {\textbf{x}}_{\textrm{A}_j}\Vert }{\textbf{u}}^{n+1}_{\textrm{A}_j}}{\sum ^{4}_{j = 1}\frac{1}{\Vert {\textbf{x}}_{\textrm{a}_k} - {\textbf{x}}_{\textrm{A}_j}\Vert }}, \end{aligned}$$

(40a)

$$\begin{aligned} \dot{{\textbf{u}}}^{n+1}_{\textrm{a}_{k}}&= \frac{\sum ^{4}_{j = 1}\frac{1}{\Vert {\textbf{x}}_{\textrm{a}_k} - {\textbf{x}}_{\textrm{A}_j}\Vert }\dot{{\textbf{u}}}^{n+1}_{\textrm{A}_j}}{\sum ^{4}_{j = 1}\frac{1}{\Vert {\textbf{x}}_{\textrm{a}_k} - {\textbf{x}}_{\textrm{A}_j}\Vert }}, \end{aligned}$$

(40b)

in the elasticity problem, and such as:

$$\begin{aligned} C^{n+1}_{\textrm{a}_{k}} = \frac{\sum ^{4}_{j = 1}\frac{1}{\Vert {\textbf{x}}_{\textrm{a}_k} - {\textbf{x}}_{\textrm{A}_j}\Vert }C^{n+1}_{\textrm{A}_j}}{\sum ^{4}_{j = 1}\frac{1}{\Vert {\textbf{x}}_{\textrm{a}_k} - {\textbf{x}}_{\textrm{A}_j}\Vert }}, \end{aligned}$$

(41)

in the diffusion problem.

3.3.2 The switching strategy

In the present study, the use of computational resources is optimized by implementing an adaptive algorithm capable of tracking the evolution of critical regions (e.g., the morphology of damage in time) by dynamically replacing regions represented by the collocation scheme and discretized with a coarse grid with regions described by the standard scheme and discretized with a fine grid. Recalling the domains $\Omega ^{+}$ and $\Omega ^{-}$ introduced in the previous section, the main purpose of the strategy is to adaptively switch the configuration at active regions of $\Omega ^{+}$ where discontinuities may coalesce or propagate, so as to ensure that coalescence and propagation of discontinuities take place within active regions of the $\Omega ^{-}$ domain. The adaptive switching is therefore performed by deactivating nodes in $\Omega ^{+}$ and consequently activating nodes in $\Omega ^{-}$ accordingly, while identifying appropriate fictitious nodes in both domains (see Fig. 6). The identification of the critical zones, whose configuration needs to be switched, requires the definition of a suitable criterion for the triggering of the adaptive algorithm. Inspired by Shojaei et al. (2016), Shojaei et al. (2022), Mossaiby et al. (2022), Sheikhbahaei et al. (2023), the criterion employed in the present work is based on the status of the stretch at each bond. Recalling the definition of bond stretch in (6) and considering two generic neighboring nodes ${\textbf{x}}_{i}$ and ${\textbf{x}}_{j}$ in the initial or reference configuration of the system, at a time instant $t^{n}$, the linking bond between the two nodes is considered to be critical if the value of its stretch falls within the following range:

$$\begin{aligned} \chi s_{0} \le \frac{\bigg \Vert \left( {\textbf{x}}_{j} + {\textbf{u}}^{n}_{j} \right) - \left( {\textbf{x}}_{i} + {\textbf{u}}^{n}_{i} \right) \bigg \Vert }{\Vert {\textbf{x}}_{j}-{\textbf{x}}_{i} \Vert }-1 \le s_{0}, \end{aligned}$$

(42)

where $0< \chi < 1$ is a factor which indicates how conservative the switching criterion is and which is usually selected to be around 0.9 (Mossaiby et al. 2022), while $s_{0}$ is the critical stretch, as defined in Sect. 2.1. If the bond connecting nodes ${\textbf{x}}_{i}$ and ${\textbf{x}}_{j}$ is identified as critical, the union of their neighborhoods is considered as a critical zone and, consequently, both the discretization scheme and the grid spacing employed to describe this region are respectively switched to the standard scheme and fine grid spacing.

The discretized form of the switching strategy is illustrated in Fig. 6 to give a clearer view of how the algorithm works. The configuration of $\Omega ^{-}$ and $\Omega ^{+}$ near a critical region of a generic domain at time instant $t^{n}$ is depicted at the top of Fig. 6. In this framework, once the adaptive algorithm identifies the linking bond between a pair of nodes ${\textbf{x}}_{1}$ and ${\textbf{x}}_{2}$ in the coarse grid as critical (cf. (42)), before proceeding to the next time instant $t^{n+1}$, the configuration of both $\Omega ^{-}$ and $\Omega ^{+}$ needs to be updated. As schematically represented in Fig. 6, this is performed by deactivating the nodes located within the switching area in $\Omega ^{+}$, i.e., within the area formed by the union of the neighborhoods of nodes ${\textbf{x}}_{1}$ and ${\textbf{x}}_{2}$, and accordingly, by activating some nodes within the same area in $\Omega ^{-}$.

Activation and deactivation of nodes is followed by the identification of appropriate fictitious nodes in both domains. The updated configuration of both $\Omega ^{-}$ and $\Omega ^{+}$ at time instant $t^{n+1}$ is showed at the bottom of Fig. 6. Further details regarding the implementation of the adaptive algorithm are provided in Mossaiby et al. (2022).

It is important to highlight that, even if the switching strategy restricts the application of the standard scheme and the fine grid spacing only to localized regions of the domain, the implementation of the adaptive algorithm is more convenient for problems involving fast and uncertain evolution of discontinuities, such as in the case of dynamic crack propagation, than for problems where the evolution of the critical regions is slower and more predictable, such as in the case of bio-degradation processes. This is due to the fact that the triggering of the algorithm adds a certain overhead to the model. In light of this, in the numerical examples presented in Sect. 4, the switching strategy is implemented only in the dynamic brittle fracture case study, whereas, in the corrosion problem, the $\Omega ^{-}$ and $\Omega ^{+}$ domains are defined a priori and remain unchanged during the simulation. Beyond that, in corrosion problems, the introduction of a finer grid in correspondence of the phase boundaries, either in a fixed or adaptive configuration, is necessary and of key importance for an accurate simulation of the volume loss in the vicinity of the corrosion layer.

4 Numerical examples

In this section, the performance of the proposed multi-adaptive scheme is examined by means of two real-world examples about dynamic crack propagation and corrosion. In the first example, i.e., the Kalthoff–Winkler experiment, the solution of the proposed scheme, referred to as (adaptive, hybrid), with grid spacing $\Delta x$ equal to $\Delta x^{-}$ within the critical region and equal to $\Delta x^{+}$ for the remaining, is compared with those of three other approaches: (uniform, coarse) that applies the standard scheme to a uniform discretization with grid spacing equal to $\Delta x^{+}$, (uniform, fine) that applies the standard scheme to a uniform grid with grid spacing equal to $\Delta x^{-}$, and (adaptive, standard) which is based on the multi-grid approach introduced in Shojaei et al. (2018) and applies the standard scheme to a non-uniform discretization similar to that of the proposed approach.

After validating the capabilities of the (adaptive, hybrid) scheme compared to the other approaches, in the second example, i.e., the three-dimensional corrosion problem, the solution of the proposed approach is compared only with that of the (uniform, fine) model.

The solution of the (uniform, fine) approach is in fact considered here as the reference one since, thanks to the high level of refinement of the grid employed for the discretization, it is the model that most accurately reproduces the physics of the problems.

In this work, high values of m have been chosen (particularly in the first example) to prove the capability and effectiveness of the proposed multi-adaptive approach in dealing with problems in which the characteristic length scale of the material or the phenomena under investigation is large, i.e., the horizon $\delta$ takes large values, and the required resolution is also high.

All the approaches are implemented through an in-house code developed using the C++ programming language. Inspired by the study in Mossaiby et al. (2022, 2017) and the PD codes by Mossaiby et al. in Mossaiby (2017, 2022), the developed code is massively parallelized. All the simulations are performed on a computational node of an in-house high performance computing (HPC) cluster including two sockets with a 24-core 2.1 GHz Intel Xeon Scalabe Platinum 8160 processor. By employing OpenMP directives, a shared memory multiprocessing parallelism on up to 48 cores is achieved. The comparison of the run times of the different solutions is carried out by excluding I/O times from the total timing. To study the influence of parallelism on the speed up achieved by the proposed approach, in the first example, the run times are reported for two scenarios regarding parallelism on 12 and 48 cores. In the second example, the run times are instead reported only for the case of parallelism on 48 cores.

4.1 Example 1: Kalthoff–Winkler experiment

The problem considered in the first example is the Kalthoff–Winkler experiment (Kalthoff 2000), a well-known problem which has been the subject of numerous studies concerning dynamic fracture modeling of brittle materials, also in the PD framework (Shojaei et al. 2018; Zaccariotto et al. 2018; Dipasquale et al. 2014; Ren et al. 2017, 2019; Islam and Shaw 2020; Ning et al. 2022). Figure 7 (left) schematically represents the geometry of the problem, which consists of a rectangular steel plate with two parallel pre-cracks subjected to an impact load from a rigid projectile which laterally hits the plate at a boundary region between the pre-cracks. As comprehensively described in Kalthoff (2000), it is experimentally observed that the fracture type depends on the impact speed. If the plate is made of steel 18Ni1900, as in this case study, an impact speed of $32 \times 10^{3}$ mm/s causes a brittle fracture mainly in mode I. In fact, once the impact takes place, cracks start to propagate from the pre-cracks tips and grow almost straightly, at an angle of approximately $68^{\circ }$ with respect to the horizontal direction, until they approach the plate boundaries.

Fig. 7

Schematic representation of (left) the problem domain in Example 1, and (right) the initial configuration of the adaptive approaches

Fig. 8

Representation of the PD neighborhood with different discretization schemes employed in Example 1. The calculation in the standard scheme runs over 1793 and 441 nodes for neighborhoods within the fine and coarse grids. However, in the hybrid discretization the calculation runs over only 49 collocation nodes for the neighborhoods within the coarse grid

The values of the main problem parameters are similar to the ones reported in Dipasquale et al. (2014), i.e., $E = 190\times 10^{3}$ N/$\mathrm {mm^2}$ (Young’s modulus), $\rho = 8000\times 10^{-9}$ Kg/$\mathrm {mm^3}$ (mass density), $G_{0} = 22170\times 10^{-6}$ J/$\mathrm {mm^2}$ (fracture energy), and $\nu = 1/4$ (Poisson’s ratio) since plane strain conditions are considered. The impact load is simulated by imposing an initial speed of $v_{0} = 16.5\times 10^{3}$ mm/s on the nodes located along the portion of the left side of the plate between the two pre-cracks. The imposed speed is oriented along the horizontal direction and is kept constant throughout the entire simulation. The problem is studied by employing the four different approaches previously introduced in this section and by assuming $\Delta x^{+} = 2 \Delta x^{-} = 0.333$ mm and $\delta = 4$ mm (i.e., $m^{+} = \delta /\Delta x^{+} = 12$, $m^{-} = \delta /\Delta x^{-} = 24$, where $m^{+}$ is the ratio used in the coarse portion of the domain, whereas $m^{-}$ is the ratio employed in the fine portion of the domain). The time integration is performed by exploiting the velocity-Verlet algorithm, as mentioned in Sect. 3.1. The problem is solved for a total time duration of 87.5 $\mathrm {\mu s}$ and by taking a time step of $\Delta t = 2 \times 10^{-3}$ $\mathrm {\mu s}$. For the proposed multi-adaptive scheme, i.e., the (adaptive, hybrid) approach, in the portion of the domain discretized using the collocation scheme, the monomial basis functions used to perform the calculations are taken up to the second-order (cf. (21)) which, in two dimensions, leads to the following specifications in terms of number of monomials and number of collocation nodes, i.e., $n_{p} = 6$ and $n_{c} = 49$, respectively. Figure 8 illustrates the PD neighborhood obtained considering the different discretization schemes employed for the solution of Example 1. The figure clearly demonstrates the advantage of using the proposed scheme over the standard one since, when considering the standard scheme, PD neighborhoods within the fine and coarse grids consist of 1793 and 441 nodes, respectively, whereas in the proposed approach, PD neighborhoods within the coarse grid include only 49 collocation nodes. The configuration of the (adaptive, hybrid) and (adaptive, standard) approaches at the beginning of the simulation is schematically represented in Fig. 7 (right). The black color is used to represent the $\Omega ^{-}$ domain, which includes the pre-cracks and the boundaries. As aforementioned, in the (adaptive, hybrid) approach, $\Omega ^{-}$ and $\Omega ^{+}$ are discretized using the standard and collocation schemes, respectively, whereas, in the (adaptive, standard) approach, both domains are discretized through the standard scheme. As for the adaptive algorithm to be exploited in the adaptive approaches, the factor $\chi$ (cf. (42)) is set to be equal to 0.95.

Figure 9 illustrates the crack pattern obtained by the four models considered in the study and the evolving configuration of the $\Omega ^{-}$ domain for the two adaptive approaches at four different time instants. Similar damage contour plots are obtained for all models except the (uniform, coarse) one since, in this case, both the crack propagation angle and speed are slightly different from those simulated by the other approaches. Moreover, in this case, a secondary fracture originates at the side of the plate opposite to the impacted one. This type of phenomenon is instead not reported by the other models. The solution obtained by the (adaptive, hybrid) approach is therefore in excellent agreement with those of the (uniform, fine) and (adaptive, standard) approaches, thus confirming the applicability of the proposed multi-adaptive scheme to the study of dynamic crack propagation problems. To further validate the proposed scheme, the contour plots of the velocity field along the vertical direction obtained by the four different models at the same time instants considered in Fig. 9 are depicted in Fig. 10. Also in this case, it is demonstrated that the result obtained by the (adaptive, hybrid) scheme is in very good agreement with those of the (uniform, fine) and (adaptive, standard) approaches. The discrepancies in the solution obtained by the (uniform, coarse) model with respect to the other approaches are also reflected in the velocity field.

Fig. 9

The crack pattern obtained by different models in Example 1; the evolution of the $\Omega ^{-}$ domain for the (adaptive, standard) and (adaptive, hybrid) approaches is also included

Fig. 10

Contour plots of the velocity field along the vertical direction, at four time instants, obtained by the four approaches: (uniform, coarse), (uniform, fine), (adaptive, standard), and (adaptive, hybrid) in Example 1; the unit is [mm/s]

The numerical efficiency of the (adaptive, hybrid) model is highlighted by comparing its computational cost with those of the (uniform, fine) and (adaptive, standard) approaches. Table 1 reports the number of active nodes in each domain (i.e., $\Omega ^{+}$ and $\Omega ^{-}$ for the adaptive approaches) at the beginning and at the end of the simulation and the run times of the three aforementioned models. To get a better view of the performance of the proposed multi-adaptive scheme, the speed ups are also presented. Run times and relative speed ups for two different configurations of parallelism, i.e., on 12 and 48 cores, are reported in order to investigate the level of influence that the parallelism has on the speed up achievable by the adaptive approaches over the (uniform, fine) model. As shown in Table 1, when running the simulations on 12 cores, both adaptive schemes turn out to be 1.86 times faster than the (uniform, fine) approach, whereas, when the simulations run on 48 cores, the (adaptive, hybrid) scheme is the most computationally efficient approach, since it is 1.19 times faster than the (uniform, fine) model and almost 1.09 times faster than the (adaptive, standard) scheme. Even

Table 1 Run times for Example 1. ($2 \Delta x^{-} = \Delta x^{+} = 0.333$ mm)

Fig. 11

Comparison of the energy content of the system, within a circular region with radius equal to 10 mm centered at the upper pre-crack tip, for the four approaches: (uniform, coarse), (uniform, fine), (adaptive, standard), and (adaptive, hybrid) in Example 1

though the optimization of the computational resources related to the use of the two adaptive approaches is more evident when the simulations are performed exploiting 12 cores, the use of more cores highlights the higher efficiency of the proposed scheme in comparison to the adaptive strategy based on the standard scheme. Considering the results reported in Table 1 and recalling Figs. 9 and 10, it is possible to conclude that the multi-adaptive scheme is able to accurately reproduce the reference solution, i.e., the solution of the (uniform, fine) approach, at a remarkably lower computational cost.

To further validate the performance of the multi-adaptive approach, Fig. 11 illustrates the variation in the energy content of the system throughout the entire duration of the simulation for the four different models considered in the study. For each approach, the energy content is computed within a circular region located at the tip of the upper pre-crack. As can be inferred from Fig. 11, the result obtained by the (adaptive, hybrid) model is in very good agreement with those of the (uniform, fine) and (adaptive, standard) approaches, thus indicating that the proposed scheme is capable of modeling crack nucleation and crack propagation speed with the same accuracy as the aforementioned models but, as shown in Table 1, outperforming them in terms of computational efficiency.

4.2 Example 2: Three-dimensional corrosion problem

The second example presented in this work concerns the bio-degradation of a magnesium bone implant screw. Over the last decades, this problem has attracted rapidly increasing attention, since magnesium implants combine bone-like mechanical and osteoconductive properties with a favourable bio-compatibility (Negrescu et al. 2020). Moreover, as they naturally degrade in the living organisms due to bio-corrosion, they can be used as temporary mechanical supports that don’t need to be removed in a second surgical intervention after healing of the surrounding tissue but that naturally dissolve over time. Unfortunately, to date, the progress in the development of such implants is still greatly impeded by the high complexity of their application, where chemical, mechanical, and biological factors interact, and by the considerable cost associated with related experimental studies. Numerical modeling is therefore increasingly seen as the most promising tool to overcome these limitations (Gartzke et al. 2020; Ma et al. 2018). Despite the successful developments based on classical local methods, PD diffusion solvers are more suitable for modeling the bio-degradation process since, in these corrosion problems, the concentration field in correspondence of the corrosion front is in fact affected by a high level of discontinuity, thus making it difficult for classical local diffusion models to adequately treat this kind of phenomena. PD models can instead conveniently capture the evolution of phase boundaries (e.g., corrosion interfaces) as a natural outcome of their solution (Hermann et al. 2022). Even though the application of the proposed approach is here restricted to the modeling of uniform corrosion (see Jafarzadeh et al. (2019b) for a different approach to uniform corrosion modeling), in the last decade PD has been extensively employed to model different types of corrosive phenomena, such as pitting corrosion (Chen and Bobaru 2015a; Jafarzadeh et al. 2019a; Wang et al. 2023), pitting corrosion with lacy covers (Jafarzadeh et al. 2019c), intergranular corrosion (Jafarzadeh et al. 2018), galvanic corrosion (Zhao et al. 2021), crevice corrosion (Jafarzadeh et al. 2022), stress-assisted corrosion (Jafarzadeh et al. 2019b; Fan et al. 2022), and stress-corrosion cracking (Chen et al. 2021). The extension of the proposed approach to the simulation of other corrosion processes and damage problems is foreseen for the future.

Fig. 12

Schematic representation of the problem domain and initial configuration in Example 2

The three-dimensional problem considered in this example consists of a metallic specimen, i.e., the Mg-10Gd implant screw depicted in Fig. 12, immersed in a sphere filled with a liquid electrolyte. The implant screw is characterized by a radius of 1 mm, a height of 4 mm, and a $0.5 \times 0.5$ mm slotted head. The radius of the sphere is taken here equal to 6 mm, the radius and height of the cylindrical $\Omega ^{-}$ domain are 2.1 mm and 6.2 mm, respectively, whereas the initial concentrations of the solid (i.e., the intact metal) and liquid (i.e., the electrolyte) phases are $C_{\textrm{sol}}=6.26\times 10^{-5} \text { mol/mm}^3$ and $C_{\textrm{liq}}=0 \text { mol/mm}^3$, respectively. Due to the corrosion process induced by the electrolyte on the metal, the solid phase reduces and the dissolved material gradually diffuses into the liquid phase through the so-called dissolution flux. To make the PD diffusion model (see Sect. 2.2) suitable for the simulation of the corrosion process, it is necessary to introduce two micro-diffusivity parameters, i.e., $\kappa _{\textrm{liq}}$ and the micro-dissolvability $\kappa _{\textrm{int}}$, which correspond to the bonds connecting pairs of material points belonging to the liquid phase and to the interfacial bonds connecting material points in the solid phase with material points in the liquid phase, respectively. In the solid phase, no flux between pairs of material points is considered. Another input parameter employed for the modeling of the corrosion process is represented by the threshold concentration $C_{\textrm{sat}}$. This parameter is exploited to determine the concentration of the solid phase throughout the dissolution process. To be more specific, once the concentration in correspondence of a material point in the solid phase becomes lower than this threshold value, the phase of that material point is changed from solid to liquid. Thanks to this phase-changing mechanism, the corrosion front can autonomously evolve during the simulation.

Fig. 13

Representation of the PD neighborhood with different discretization schemes employed in Example 2. The calculation in the standard scheme runs over 7153 nodes for neighborhoods within the fine grid. In the hybrid approach, the calculation runs over only 123 collocation nodes for the neighborhoods within the coarse grid

The values of the main problem parameters are $\kappa _{\textrm{liq}}=7.98\times 10^{-5}\text { } \textrm{s}^{-1}\textrm{mm}^{-2}$, $\kappa _{\textrm{int}}=2.81\times 10^{-6}\text { } \textrm{s}^{-1}\textrm{mm}^{-2}$, $C_{\textrm{sat}}=6.26\times 10^{-10} \text { mol/mm}^3$, and $q=1$ (cf. (12)). Dirichlet-type boundary conditions are enforced by assuming a constrained concentration equal to $0 \text { mol/mm}^3$ at all nodes located within a finite distance from the surface of the sphere, here considered equal to the horizon (see Sect. 2.2). The problem is studied by employing two of the previously introduced approaches, i.e., the (uniform, fine) and (adaptive, hybrid) models, and by assuming $\Delta x^{+}=2\Delta x^{-}=0.075$ mm and $\delta =~0.45$ mm (i.e., $m^{+} = \delta /\Delta x^{+} = 6$, $m^{-} = \delta /\Delta x^{-} = 12$, where $m^{+}$ is the ratio used in the coarse portion of the domain, whereas $m^{-}$ is the ratio employed in the fine portion of the domain). To be consistent with the discussion carried out in the Example 1 presented in Sect. 4.1, the proposed multi-adaptive scheme is also here referred to as (adaptive, hybrid), although in this case, as already mentioned, the adaptive algorithm is not triggered during the simulation of the corrosion process. In the proposed approach, the configuration of the $\Omega ^{-}$ and $\Omega ^{+}$ domains represented in Fig. 12 is in fact defined a priori and remains fixed throughout the entire simulation. The $\Omega ^{-}$ domain, which is discretized through the standard scheme, is set in order to cover only the portion of the domain where the concentration field is discontinuous, i.e., the area in correspondence of which diffusion between nodes characterized by a different phase takes place (phase boundaries). In the portion of the domain discretized using the collocation scheme (i.e., the $\Omega ^{+}$ domain), the monomial basis functions used to perform the calculations are taken up to the second-order (cf. (21)) which, in three dimensions, leads to the following specifications in terms of number of monomials and number of collocation nodes, i.e., $n_{p} = 10$ and $n_{c} = 123$, respectively. Figure 13 represents the PD neighborhood obtained considering the different discretization schemes employed for the solution of Example 2. The figure clearly demonstrates the advantage of using the proposed approach over the (uniform, fine) one since, when considering the standard scheme, PD neighborhoods within the fine grid consist of 7153 nodes, whereas in the proposed approach, PD neighborhoods within the coarse grid include only 123 collocation nodes. The time integration is performed by exploiting the explicit forward Euler algorithm recalled in Sect. 3.1 (cf. (17)). The problem is solved for a total time duration of 14 $\textrm{days}$ and by considering a time step of $\Delta t = 90$ $\textrm{s}$.

The results of the PD corrosion simulation for the Mg-10Gd implant screw over 14 days of immersion in the liquid electrolyte are illustrated in Fig. 14. The figure shows the concentration profile of both the solid metal and dissolved material diffused within the liquid phase obtained by the two models considered in the study at two different time instants. For the sake of clarity, solid and liquid phases are represented separately, and only half of the liquid sphere is shown. The reported results demonstrate that the solution obtained by the (adaptive, hybrid) scheme is in excellent agreement with the reference one, since both the corrosion patterns discernible in the solid phase and the dissolved material diffusion within the liquid phase almost perfectly match the ones simulated by the (uniform, fine) approach. The results therefore confirm the applicability of the proposed multi-adaptive scheme to the modeling of the corrosion process in large-scale, geometrically complex problems. To further validate the proposed approach, Fig. 15 shows the results obtained in terms of relative volume loss of the solid phase over time for the two aforementioned models. For computational cost issues, the solution of the (adaptive, hybrid) scheme is validated by that of the (uniform, fine) approach within the first 2 days of corrosion. It can be inferred that the proposed approach recaptures the reference corrosion rate. Nonetheless, the simulation of the (adaptive, hybrid) scheme is continued for 14 days of bio-degradation. A glimpse into the results reveals that more than $40\%$ of the solid phase dissolves after 14 days of corrosion.

Fig. 14

Contour plots of the concentration field, at two time instants, obtained by the two approaches: (uniform, fine) and (adaptive, hybrid) in Example 2; the unit is [mol/mm$^3$]. The lighter color of the $\Omega ^{+}$ domain in the (adaptive, hybrid) scheme with respect to that of the same region in the (uniform, fine) solution is just a visual effect related to the coarser grid spacing employed to discretize that portion of the domain

The numerical efficiency of the (adaptive, hybrid) scheme is highlighted by comparing its computational cost with that of the (uniform, fine) approach. Table 2 reports the number of active nodes in each domain (i.e., $\Omega ^{+}$ and $\Omega ^{-}$ for the adaptive approach) and the average run times (per 100 time steps) of the two aforementioned models. To get a better view of the performance of the proposed multi-adaptive scheme, the average speed ups (per 100 time steps) are also presented. Run times and relative speed ups are reported for the case of parallelism on 48 cores. As shown in Table 2, the (adaptive, hybrid) scheme turns out to be 11.76 times faster than the (uniform, fine) approach. Considering these results and recalling Figs. 14 and 15, it is possible to conclude that the proposed multi-adaptive scheme is capable of accurately reproducing the solution of the (uniform, fine) approach, at a considerably lower computational cost.

Fig. 15

Relative volume loss of the solid phase over time obtained by the two approaches: (uniform, fine) and (adaptive, hybrid) in Example 2

Table 2 Run times for Example 2. ($2 \Delta x^{-} = \Delta x^{+} = 0.075$ mm)

The results reported in Tables 1 and 2 show that the speed up achieved by the (adaptive, hybrid) scheme for the three-dimensional corrosion example is much larger than the ones obtained for the two-dimensional dynamic crack propagation example. This is related to the fact that, in the corrosion problem, the overhead related to the triggering of the adaptive algorithm is not present, since the $\Omega ^{-}$ and $\Omega ^{+}$ domains are defined a priori and remain unchanged throughout the entire simulation.

5 Conclusions

This paper presents a multi-adaptive approach to enhance the numerical performance of PD models and thus optimize the use of computational resources. In the proposed framework, the application of the standard scheme, a particle-based method commonly exploited to implement PD models, is restricted to localized regions affected by the presence of discontinuities or with complex geometrical details (i.e., critical regions) and boundaries, while a recently proposed collocation scheme is instead employed for the remaining part of the domain.

The reason behind the implementation of this hybrid discretization is that, despite the advantages of the collocation scheme in terms of computational cost and computation of spatial integrals, this scheme may be affected by a loss of accuracy in the proximity of critical regions and close to the boundary of the body, where, instead, the standard scheme is known to perform better due to its capability to conveniently calculate the required integral terms in regions described by a nonlinear PD model, and thus to handle material separation.

With the aim of maximizing the numerical efficiency of PD models, this hybrid discretization scheme is implemented here in conjunction with a multi-grid method in which grids with different spacings are coupled within the same domain, thus limiting the application of a fine grid spacing only to the small portions of the domain in which it is required (e.g., critical regions and boundaries). The advantages of both the hybrid discretization scheme and the multi-grid approach are therefore combined within the proposed multi-adaptive framework, whose capabilities in dealing with dynamic brittle fracture and corrosion problems in two and three dimensions are assessed through two real-world numerical examples. In the examples provided, which consist of modeling the Kalthoff–Winkler experiment and the bio-degradation of a magnesium bone implant screw, it is proved that, for given accuracy requirements, the proposed multi-adaptive scheme is capable of reproducing the solution obtained by a PD model, discretized using the standard scheme and with a very fine grid spacing, at a significantly lower computational cost. It is also demonstrated that the efficiency of the developed scheme is even more pronounced in large-scale, geometrically complex, three-dimensional problems involving millions of degrees of freedom.