Numerical investigation of statistical variation of concrete damage properties between scales

Abstract

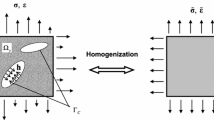
Concrete is typically treated as a homogeneous material at the continuum scale. However, the randomness in micro-structures has profound influence on its mechanical behavior. In this work, the relationship of the statistical variation of macro-scale concrete properties and micro-scale statistical variations is investigated. Micro-structures from CT scans are used to quantify the stochastic properties of a high strength concrete at the micro-scale. Crack propagation is then simulated in representative micro-structures subjected to tensile and shear tractions, and damage evolution functions in the homogenized continuum are extracted using a Helmholtz free energy correlation. A generalized density evolution equation is employed to represent the statistical variations in the concrete micro-structures as well as in the associated damage evolution functions of the continuum. This study quantifies how the statistical variations in void size and distribution in the concrete microstructure affect the statistical variation of material parameters representing tensile and shear damage evolutions at the continuum scale. The simulation results show (1) the random variation decreases from micro-scale to macro-scale, and (2) the coefficient of variation in shear damage is larger than that in the tensile damage.

Appendix

As discussed in Sect. 2, the damage evolution functions are extracted from the micro-cell simulation using energy bridging. These damage evolution functions are used in the elastic damage model of concrete. The plastic behavior of concrete under compression (Ortiz 1985; Faria et al. 1998; Lee and Fenves 1998) is also considered in this work. Under the continuum damage mechanics framework (Faria et al. 1998; Wu et al. 2006), the total HFE $\bar{{\psi }}^{m}$ can be expressed as the sum of the elastic HFE $\bar{{\psi }}^{e}$ from the micro-cell simulation and plastic HFE.

$$\begin{aligned} \bar{{\psi }}^{m}=\bar{{\psi }}^{e}+\bar{{\psi }}^{p} \end{aligned}$$

(49)

In Eq. (49), the elastic HFE can be expressed as

$$\begin{aligned} \bar{{\psi }}^{e}=\frac{1}{2}\bar{{{\varvec{\sigma }}}}:\bar{{{\varvec{\varepsilon }}}}^{e} \end{aligned}$$

(50)

where $\bar{{{\varvec{\varepsilon }}}}^{e}=\bar{{{\varvec{\varepsilon }}}}-\bar{{{\varvec{\varepsilon }}}}^{p}$. A decomposition of the effective stress is given as

$$\begin{aligned} \bar{{{\varvec{\sigma }} }}={\varvec{C}}_0 :\left( {\bar{{{\varvec{\varepsilon }} }}-\bar{{{\varvec{\varepsilon }} }}^{P}} \right) ={\varvec{C}}_0 :\bar{{{\varvec{\varepsilon }} }}^{e}=\bar{{{\varvec{\sigma }} }}^{vol}+\bar{{{\varvec{\sigma }} }}^{dev} \end{aligned}$$

(51)

where $\bar{{{\varvec{\sigma }} }}^{vol}$ and $\bar{{{\varvec{\sigma }} }}^{dev}$ are the effective deviatoric and volumetric stresses, respectively. Comparing Eqs. (50) with (20), $\bar{{\psi }}^{e}$ can be replaced by $\bar{{\psi }}$ ($\bar{{\psi }}^{e}=\bar{{\psi }}$) when the elastic micro-cell analysis is performed ($\bar{{{\varvec{\varepsilon }} }}=\bar{{{\varvec{\varepsilon }} }}^{e}$). According to the experimental results (Ortiz 1985; Faria et al. 1998; Lee and Fenves 1998), concrete shows little, almost no plastic strain under tension. Therefore, Eq. (49) can be rewrite as

$$\begin{aligned} \bar{{\psi }}^{m}\left( {\bar{{\varepsilon }}^{e},\bar{{\varepsilon }}^{p},{{\varvec{\upkappa }} },d^{t},d^{s}} \right)= & {} \bar{{\psi }}^{e}\left( {\bar{{\varepsilon }}^{e},d^{t},d^{s}} \right) \nonumber \\&+\,\bar{{\psi }}^{p}\left( {\bar{{\varepsilon }}^{e},\bar{{\varepsilon }}^{p},{{\varvec{\upkappa }} },d^{s}} \right) \end{aligned}$$

(52)

where ${\varvec{\kappa }}$ denotes a suitable set of plastic variables, and $d^{t}$ and $d^{s}$ are tensile and shear damage parameters, respectively.

The elastic and plastic HFE’s are defined as

$$\begin{aligned}&\bar{{\psi }}^{e}\left( {\bar{{{\varvec{\varepsilon }}}}^{e},d^{t},d^{s}} \right) =\int _0^{\bar{{\varepsilon }}^{e}} \left[ \left( {1-d^{t}} \right) \bar{{{\varvec{\sigma }} }}^{vol}\right. \nonumber \\&\left. +\left( {1-d^{s}} \right) \bar{{{\varvec{\sigma }} }}^{dev} \right] :d\bar{{{\varvec{\varepsilon }} }}^{e} \end{aligned}$$

(53)

$$\begin{aligned}&\bar{{\psi }}^{p}\left( {\bar{{\varepsilon }}^{e},\bar{{\varepsilon }}^{p},{\varvec{\kappa }} ,d^{s}} \right) =\left( {1-d^{s}} \right) \int _0^{\varepsilon ^{p}} {\bar{{{\varvec{\varepsilon }} }}^{e}} :C_0 :d\bar{{\varepsilon }}^{p}\nonumber \\ \end{aligned}$$

(54)

According to the second principle of thermodynamics, any arbitrary irreversible process satisfies the (Coleman and Gurtin 1967) inequality, of which the reduced form is

$$\begin{aligned} \dot{\gamma }=-\dot{\bar{{\psi }}}^{m}+\bar{{{\varvec{\sigma }}}}:\dot{\bar{{{\varvec{\varepsilon }}}}}\ge 0 \end{aligned}$$

(55)

Referring to the standard thermodynamics arguments by Coleman and Gurtin (1967) and the assumption that damage and plastic unloading are elastic processes, the following conditions are satisfied for any admissible process as:

$$\begin{aligned} \bar{{{\varvec{\sigma }}}}= & {} \frac{\bar{{\psi }}^{e}}{\partial \bar{{{\varvec{\varepsilon }}}}^{e}} \end{aligned}$$

(56)

$$\begin{aligned} \dot{\gamma }^{d}= & {} \left( {\frac{\partial \bar{{\psi }}^{m}}{\partial d^{t}}\dot{d}^{t}+\frac{\partial \bar{{\psi }}^{m}}{\partial d^{s}}\dot{d}^{s}} \right) \ge 0 \end{aligned}$$

(57)

$$\begin{aligned} \dot{\gamma }^{p}= & {} \left( {\bar{{{\varvec{\sigma }}}}:\dot{\bar{{{\varvec{\varepsilon }} }}}^{p}+\frac{\partial \bar{{\psi }}^{m}}{\partial {\varvec{\kappa }} }\dot{{\varvec{\kappa }} }} \right) \ge 0 \end{aligned}$$

(58)

It can be clearly seen in Eq. (56), the homogenized stress is only dependent on the elastic HFE. Taking Eq. (56) into consideration, the damage evolution is assumed to be only associated with the elastic HFE, and the independent evolution model can be introduced for the plastic deformation. It is noted that Eqs. (57) and (58) express the irreversible damage and plastic processes. The construction of damage evolution functions follow the energy bridging procedures described in Eqs. (27) and (28).

The Advanced Fundamental Concrete (AFC) model (Adley et al. 2010) coupled with the tension and shear damage evolution functions (Lin et al. 2016) is employed in this paper as the concrete material model. In this modified AFC model, when the first invariant of the stress tensor ($I_1$) is less than or equal to zero, the yield surface is expressed as

$$\begin{aligned} Y_c= & {} \left\| {\bar{{{\varvec{\sigma }}}}^{dev}} \right\| -\left( C_1 -\left( {C{ }_2+\left( {C_1 -C_2 } \right) d^{s}} \right) e^{A_n I_1 }\right. \nonumber \\&\left. -\,C_4 I_1 \right) \left( {1+C_3 \ln (\dot{\bar{{\varepsilon }}}_n^{dev} )} \right) \end{aligned}$$

(59)

where $C_1 , C_2 , {C_3 } , {C_4 }$ and $A_n$ are the parameters related to the initial yield surface and confinement state, $\dot{\bar{{\varepsilon }}}_n^{dev} =\frac{\bar{{\varepsilon }}}{\bar{{\varepsilon }}_0^t }$ is the effective deviatoric strain rate (Shkolnik 2008) normalized by a reference strain rate $\bar{{\varepsilon }}_0^t$. Based on the assumption in AFC model (Adley et al. 2010), the value of $\left( {C_1 -C_2 } \right)$ represents the initial yield point.

To capture the hardening of the concrete under compression, we modify the parameter $C_1$ as

$$\begin{aligned} C_1= & {} C_1^*(1+h\bar{{\varepsilon }}^{p}) \end{aligned}$$

(60)

$$\begin{aligned} h= & {} \left\{ {{\begin{array}{ll} h_a &{} \left\| {\bar{{{\varvec{\sigma }}}}^{dev}} \right\| \le \sigma _d \\ h_b &{} \left\| {\bar{{{\varvec{\sigma }}}}^{dev}} \right\| \ge \sigma _d \\ \end{array} }} \right. \end{aligned}$$

(61)

where $\sigma _d$ is the damage initiation stress which is assumed to be a function of the first invariant of the stress tensor ($I_1$):

$$\begin{aligned} \sigma _d =a_1 +a_2 I_1 +a_3 I_1^2 \end{aligned}$$

(62)

According to the “effective stress space plasticity” (Faria et al. 1998; Wu et al. 2006), the evolution law of plastic strain is expressed as follows:

$$\begin{aligned} \dot{\bar{{{\varvec{\varepsilon }}}}}^{p}=\dot{\lambda }^{p}\frac{\partial Y_c }{\partial \bar{{{\varvec{\sigma }}}}} \end{aligned}$$

(63)

where $\dot{\bar{{{\varvec{\varepsilon }}}}}^{p}$ is the plastic strain rate and $\dot{\lambda }^{p}$ is the plastic flow consistency parameter.

The plasticity parameters for the AFC model employed in this work are listed in Table. 1.

Table 1 Material parameters in the simulation