Abstract
There are quantum solutions for computational problems that make use of interference at some stage in the algorithm. These stages can be mapped into the physical setting of a single particle travelling through a many-armed interferometer. There has been recent foundational interest in theories beyond quantum theory. Here, we present a generalized formulation of computation in the context of a many-armed interferometer, and explore how theories can differ from quantum theory and still perform distributed calculations in this set-up. We shall see that quaternionic quantum theory proves a suitable candidate, whereas box-world does not. We also find that a classical hidden variable model first presented by Spekkens (Phys Rev A 75(3): 32100, 2007) can also be used for this type of computation due to the epistemic restriction placed on the hidden variable.




Similar content being viewed by others
Notes
It should also be noted that implementing the Deutsch–Jozsa algorithm to solve this problem on a collection of gbits (i.e. in the circuit picture) can also not be done in box-world, because the f-controlled-NOT gate will not be an allowed transformation, according to the restrictions on correlating dynamics shown in [42].
In general balanced functions which are not negations of each other result should result in operationally distinguishable statistics for some measurements, even if they all satisfy
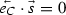 . This can be conceptually understood by discarding half of the branches and performing interferometry on the remaining half: the choice of branches included in the subset in will general govern whether the subset is balanced, constant or neither, and if it was one of the first two, then a lower-dimension version of the algorithm should work on these. It would thus be disingenuous if all balanced functions resulted in the same statistics.
. This can be conceptually understood by discarding half of the branches and performing interferometry on the remaining half: the choice of branches included in the subset in will general govern whether the subset is balanced, constant or neither, and if it was one of the first two, then a lower-dimension version of the algorithm should work on these. It would thus be disingenuous if all balanced functions resulted in the same statistics.
References
Deutsch, D.: Quantum theory, the church-turing principle and the universal quantum computer. Proc. R. Soc. A 400(1818), 97–117 (1985)
Deutsch, D., Jozsa, R.: Rapid solution of problems by quantum computation. Proc. R. Soc. Lond. A. 439(1907), 553–558 (1992)
Simon, D.R.: On the power of quantum computation. In: 35th Annual Symposium on Foundations of Computer Science, 1994 Proceedings, pp. 116–123 (1994)
Grover, L.K.: A fast quantum mechanical algorithm for database search. In: Proceedings of the Twenty-Eighth Annual ACM Symposium on Theory of Computing, STOC’96, pp. 212–219, New York, NY. ACM (1996)
Shor, P.W.: Polynomial-time algorithms for prime factorization and discrete logarithms on a quantum computer. SIAM J. Comput. 26(5), 1484–1509 (1997)
Cleve, R., Ekert, A.K., Macchiavello, C., Mosca, M.: Quantum algorithms revisited. Proc. R. Soc. Lond. A. 454(1969), 339–354 (1998)
Lloyd, S.: Quantum search without entanglement. Phys. Rev. A 61(1), 010301 (1999)
Zeilinger, A.: A foundational principle for quantum mechanics. Found. Phys. 29(4), 631–643 (1999)
Hardy, L.: Quantum Theory from Five Reasonable Axioms (2001)
Fuchs, C.: Quantum Foundations in the Light of Quantum Information (2001). arXiv:quant-ph/0106166v1
Masanes, Ll, Müller, M.P.: A derivation of quantum theory from physical requirements. New J. Phys. 13(6), 63001 (2011)
Chiribella, G., DAriano, G.M., Perinotti, P.: Quantum theory, namely the pure and reversible theory of information. Entropy 14(12), 1877–1893 (2012)
Barnum, H., Müller, M.P., Ududec, C.: Higher-order interference and single-system postulates characterizing quantum theory. New J. Phys. 16(12), 123029 (2014)
Clauser, J., Horne, M., Shimony, A., Holt, R.: Proposed experiment to test local hidden-variable theories. Phys. Rev. Lett. 23(15), 880–884 (1969)
Cirel’son, B.S.: Quantum generalizations of Bell’s inequality. Lett. Math. Phys. 4(2), 93–100 (1980)
Tsirelson, B.S.: Some results and problems on quantum Bell-type inequalities. Hadron. J. Suppl. 8, 329–345 (1993)
Popescu, S., Rohrlich, D.: Quantum nonlocality as an axiom. Found. Phys. 24(3), 379–385 (1994)
Popescu, S.: Nonlocality beyond quantum mechanics. Nat. Phys. 10(4), 264–270 (2014)
van Dam, W.: Nonlocality & Communication Complexity. DPhil thesis, University of Oxford (2000)
Cleve, R., van Dam, W., Nielsen, M., Tapp, A.: Quantum entanglement and the communication complexity of the inner product function. Theor. Comput. Sci. 486, 11–19 (2013)
Fernandez, J.M., Schneeberger, W.A.: Quaternionic computing (2003). arXiv:quant-ph/0307017
Lee, C.M., Barrett, J.: Computation in generalised probabilistic theories. New J. Phys. 17, 083001 (2015)
Lee, C.M., Hoban, M.J.: Bounds on the power of proofs and advice in general physical theories. Proc. R. Soc. A 472(2190), 20160076 (2016)
Lee, C.M., Selby, J.H.: Generalised phase kick-back: the structure of computational algorithms from physical principles. New J. Phys. 18, 033023 (2016)
Lee, C.M., Selby, J.H.: Deriving Grover’s lower bound from simple physical principles. New J. Phys. 18, 093047 (2016)
Sorkin, R.: Quantum mechanics as quantum measure theory. Mod. Phys. Lett. A 9, 3119 (1994)
Ududec, C., Barnum, H., Emerson, J.: Three slit experiments and the structure of quantum theory. Found. Phys. 41(3), 396–405 (2010)
Ududec, C.: Perspectives on the Formalism of Quantum Theory. PhD thesis, University of Waterloo (2012)
Garner, A.J.P., Dahlsten, O.C.O., Nakata, Y., Murao, M., Vedral, V.: A framework for phase and interference in generalized probabilistic theories. New J. Phys. 15(9), 093044 (2013)
Dahlsten, O.C.O., Garner, A.J.P., Vedral, V.: The uncertainty principle enables non-classical dynamics in an interferometer. Nat. Commun. 5, 4592 (2014)
Garner, A.J.P.: Phase and interference phenomena in generalized probabilistic theories. DPhil thesis, University of Oxford, Hilary Term (2015)
Spekkens, R.W.: Evidence for the epistemic view of quantum states: a toy theory. Phys. Rev. A 75(3), 32110 (2007)
Spekkens, R.W.: Quasi-quantization: classical statistical theories with an epistemic restriction. Quantum Theory, pp. 83–135 (2015)
Barrett, J.: Information processing in generalized probabilistic theories. Phys. Rev. A 75(3), 32304 (2007)
Nielsen, M.A., Chuang, I.L.: Quantum Computation and Quantum Information. Cambridge University Press, Cambridge (2000)
Schrödinger, E.: Zum Heisenbergschen Unschärfeprinzip. S. B. Preuß. Akad. Wiss., Physikalisch-mathematische Klasse 14, 296–303 (1930)
Robertson, H.P.: The uncertainty principle. Phys. Rev. 34(1), 163–164 (1929)
van Enk, S.J.: A toy model for quantum mechanics. Found. Phys. 37(10), 1447–1460 (2007)
Janotta, P., Lal, R.: Generalized probabilistic theories without the no-restriction hypothesis. Phys. Rev. A 87(5), 052131 (2013)
Pusey, Matthew F.: Stabilizer notation for Spekkens’ toy theory. Found. Phys. 42(5), 688–708 (2012)
Aharonov, Y., Bohm, D.: Significance of electromagnetic potentials in the quantum theory. Phys. Rev. 115(3), 485–491 (1959)
Gross, D., Müller, M., Colbeck, R., Dahlsten, O.C.O.: All reversible dynamics in maximally nonlocal theories are trivial. Phys. Rev. Lett. 104(8), 80402 (2010)
Dakic, B., Brukner, C.: The classical limit of a physical theory and the dimensionality of space (2013)
Müller, M.P., Masanes, Ll: Three-dimensionality of space and the quantum bit: an information-theoretic approach. New J. Phys. 15(5), 053040 (2013)
Garner, A.J.P., Müller, M.P., Dahlsten, O.C.O.: The complex and quaternionic quantum bit from relativity of simultaneity on an interferometer. Proc. R. Soc. A 473(2208), 20170596 (2017). https://doi.org/10.1098/rspa.2017.0596
Alfsen, E.M., Shultz, F.W.: Geometry of State Spaces of Operator Algebras. Birkhäuser, Boston (2003)
Dickson, L.E.: On quaternions and their generalization and the history of the eight square theorem. Ann. Math. Second Series 20(3), 155–171 (1919)
Graydon, M.A.: Quaternions and quantum theory. Master’s thesis, University of Waterloo (2011)
Baez, J.C.: Symplectic, Quaternionic, Fermionic (2014). http://www.math.ucr.edu/home/baez/symplectic.html
Bohm, D.: A suggested interpretation of the quantum theory in terms of “hidden” variables. I. Phys. Rev. 85(2), 166–179 (1952a)
Bohm, D.: A suggested interpretation of the quantum theory in terms of “hidden” variables. II. Phys. Rev. 85(2), 180–193 (1952b)
Norsen, Travis: The pilot-wave perspective on spin. Am. J. Phys. 82(4), 337–348 (2014)
Acknowledgements
The author is very grateful for illuminating discussions and correspondence with Felix Binder, Oscar Dahlsten, Daniela Frauchiger, Nana Liu, Markus Müller, Vlatko Vedral, and Benjamin Yadin. The author is grateful for financial support from the John Templeton Foundation and the Foundational Questions Institute. This research was undertaken whilst the author was funded by the Engineering and Physical Sciences Research Council (UK) at the University of Oxford. Some of concepts in this article have also appeared as part of the author’s DPhil thesis [31].
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix A: The Uncertainty Relation, and the Qubit State-Space
The Cauchy–Schwarz inequality, as applied to complex Hilbert spaces, states that
for complex vectors \(|\xi \rangle \) and \(|\chi \rangle \) (see, e.g. [35]). From this, we can derive a bound on the product of variances of measurement operators—that is, the Schrödinger–Robertson uncertainty relation [36, 37]—and the spherical shape of the qubit state-space when expressed as the expectation values of Pauli operators.
Consider a pair of operators A and B both acting on some quantum state \(|\psi \rangle \). Ineq. (A1) implies that \(|\langle \psi | A B |\psi \rangle |^2 \le \langle \psi | A^{\dag }A|\psi \rangle |\langle \psi | B^{\dag }B |\psi \rangle \) for any \(|\psi \rangle \). When A and B are also Hermitian, then
For Hermitian A and B, \(\left( \langle \psi |AB|\psi \rangle \right) ^{\dag }= \langle \psi |BA|\psi \rangle = \langle \psi |AB|\psi \rangle ^*\), and so \(\langle \psi |(AB+BA)|\psi \rangle \) is a real number equal to twice the real part of \(\langle \psi |AB|\psi \rangle \). Similarly, \(\langle \psi |(AB-BA)|\psi \rangle \) is purely imaginary, equal to twice the imaginary part of \(\langle \psi |AB|\psi \rangle \). Using \(|\bullet |^2 = \mathfrak {R}\mathrm {e}\left( {\bullet }\right) ^2 + \mathfrak {I}\mathrm {m}\left( {\bullet }\right) ^2\), we thus find that \(4|\langle \psi |AB|\psi \rangle |^2 = |\langle \psi |(AB+BA)|\psi \rangle |^2 + |\langle \psi |(AB-BA)|\psi \rangle |^2\). Substituting this in ineq. (A2):
where we have written the commutator \([A,B] = AB - BA\) and the anti-commutator \(\{A, B\} = AB + BA\).
Suppose we pick some state \(|\psi \rangle \), and two Hermitian observables X and Y, then the matrices \(A =: X - \langle X \rangle \mathbb {1}\) and \(B =: Y-\langle Y \rangle \mathbb {1}\) (where \(\langle \bullet \rangle := \langle \psi |\bullet |\psi \rangle \) is the expectation value of measurement \(\bullet \) of state \(|\psi \rangle \)) are also Hermitian. We may evaluate
Taking the expectation value of the above on the same state \(|\psi \rangle \) yields:
The last two expressions are the variances \(\Delta M^2 : = \langle M^2 \rangle - \langle M \rangle ^2\) of X and Y respectively.
Substituting these into the Cauchy–Schwarz inequality (ineq. (A3)) leads us then to Schrödinger’s statement of the uncertainty relation [36]:
This also implies the looser bound of the Robertson uncertainty principle [37], because \(|\langle \psi |\{A,B\}|\psi \rangle |^2\) in ineq. (A3) is never negative:
We may specialize the Schrödinger uncertainty principle of ineq. (A12) to a two-level quantum system (qubit), and choose two of the Pauli matrices
(say \(\sigma _x\) and \(\sigma _y\)) as X and Y. Using \([\sigma _x, \sigma _y] = 2i\sigma _z\), \(\{\sigma _x,\sigma _y\}=0\), \(\Delta X^2 = 1-\langle \sigma _x \rangle ^2\), and \(\Delta Y^2 = 1-\langle \sigma _y \rangle ^2\), we find
which rearranges to
Thus, when the qubit state-space is paramaterized in terms of the expectation values of Pauli matrices, the expectation values of pure states are bound by a sphere of unit radius. Closing these pure states into a convex set (i.e. by allowing mixtures), we find that all qubit states must be within the Bloch sphere.
Appendix B: Phase and Branch Locality in Quantum Theory
First, we show that the phase group of a projective measurement on an N-level quantum system is given by \(\bigoplus ^N \mathrm {U}\left( 1\right) \).
Lemma 1
For an N-level quantum system, with a projective measurement Z, whose outcomes may be expressed in terms of projectors \(\big \{Z_j =|j\rangle \langle j|\big \}_{j=1\ldots N}\) (and \(\sum _j Z_j = \mathbb {1}\)), all reversible phase operations (i.e. satisfying Definition 1) may be written in the form
Conversely, all matrices of this form are a phase operation with respect to Z.
Proof
We will use the isomorphism between states \(\vec {s}\) and density matrices \(\rho \), and between effects  and measurement operators M, such that the inner product in both cases gives the associated probability of a particular outcome (
and measurement operators M, such that the inner product in both cases gives the associated probability of a particular outcome ( ), and the fact that general reversible quantum transformations act as \(\rho \rightarrow U \rho \, U^{\dag }\) for \(U\in \mathrm {U}\left( N\right) \). This allows us rewrite the condition for a reversible phase operation with respect to
), and the fact that general reversible quantum transformations act as \(\rho \rightarrow U \rho \, U^{\dag }\) for \(U\in \mathrm {U}\left( N\right) \). This allows us rewrite the condition for a reversible phase operation with respect to  (written in the GPT framework as
(written in the GPT framework as  ) as an equivalent statement in the quantum formalism:
) as an equivalent statement in the quantum formalism:
This implies that \([U, Z_j] = 0\) for all j, and so we can write U diagonally in the basis of Z,
To show the converse, because U of the above form commutes with all elements \(Z_j\), and \(U^{\dag }U =\mathbb {1}\), we may use the cyclicity of trace to write: \({{\mathrm{tr}}}\left( Z_j U \rho \, U^{\dag }\right) = {{\mathrm{tr}}}\left( U^{\dag }Z_j \, U\rho \right) = {{\mathrm{tr}}}\left( U^{\dag }U Z_j\rho \right) ={{\mathrm{tr}}}\left( Z_j \rho \right) \), which is exactly the phase condition written in Eq. (C2). \(\square \)
From this, we can show the form an operation local to one branch must take agrees with Eq. (3):
Lemma 2
Branch locality implies that the change induced by a reversible quantum operation \(U_i\) on a branch i in a set of disjoint branches can be most generally expressed by a complex phase acting only on the ket \(|i\rangle \) associated with being in that particular branch:
Proof
For a branch i, and a state \(\rho _{\lnot i}\) that has no support on i such that
then a branch local operation \(U_i\) on branch i always satisfies
for any observable M. This implies that
The most general state that satisfies Eq. (B5) may be written in the Z basis as
According to Lemma 1, we can express a general quantum phase transformation with respect to Z as \(U = \sum _j e^{i \phi _j} |j\rangle \langle j|\), and consider its action on \(\rho _{\lnot i}\):
Therefore, for the condition in eq. (B7) to be satisfied, we require
For this to hold, it must be true for every element \(|\alpha \rangle \langle \beta |\), and this requires \(\phi _\alpha = \phi _\beta \) (or for \(\phi _\alpha \) and \(\phi _\beta \) to differ by an unmeasurable multiple of \(2\pi \)) for all \(\alpha \ne i,\beta \ne i\). A transformation \(U_i\) local to branch i thus has the form
where \(\Phi \) is some global phase that can be ignored. \(\square \)
Appendix C: Phase and Branch Locality in Quaternionic Quantum Theory
By using insights from Graydon [48], we can generalise the results of Appendix B into quaternionic quantum theory. A quaternion \(h \in \mathbb {H}\) may be written \(h = a + ib + jc + kd\) where \(a,b,c,d \in \mathcal {R}\) and i, j and k are three types of imaginary number satisfying \(ii = jj = kk = ijk = -\,1\). Conceptually, the jump from complex numbers to quaternions is like the jump from real numbers to complex numbers [47]. Moreover, in the same way that for n-dimension vector-space the orthogonal group \(\mathrm {O}\left( n\right) \) preserves an inner product between real vectors, and the unitary group \(\mathrm {U}\left( n\right) \) preserves an inner product between complex vectors, there is a group known as the symplectic group \(\mathrm {Sp}\left( n\right) \) which preserves an inner product for quaternionic vectors [49].
Before we can talk about the quaternionic phase-group, we remark that it is indeed meaningful to talk about quaternionic measurements. Much like in quantum theory, one can find positive semi-definite quaternionic matrices \(\{E_i\}\) which act as effects that assign probabilities to on quaternionic states \(\rho \) according to \(P = {{\mathrm{tr}}}\left( E_i \rho \right) \), and constitute a quaternionic measurement (guaranteed to give one outcome) when \(\sum _i E_i = \mathbb {1}\). Moreover one can find sets of N such matrices satisfying \(E_i E_j = \delta _{ij} E_i\) which constitute orthonormal projective measurements [48]. Much like the trace on complex matrices, the quaternionic trace is basis-independent, and its arguments may be cyclically rotated [48].
Lemma 3
For an N-level quaternionic quantum system, with a measurement Z which distinguishes perfectly between N possibilities, the group of diagonal quaternionic matrices
are within the group of reversible phase operations (i.e. satisfying Definition 1).
Proof
Take a set of quaternionic projectors \(\{Z_i\}\), and consider the most general reversible transformation \(S \in \mathrm {Sp}\left( d\right) \), which acts on a quaternionic state \(\rho \) as \(\rho \rightarrow S \rho S^\ddag \) (we shall use \(\ddag \) to represent the symplectic inverse such that \(S S^\ddag = S^\ddag S = \mathbb {1}\)). The phase group condition in Definition 1 may be written in terms of quaternionic states, effects and transformations as:
If \([Z_j, S]=0\) for all j, then this will automatically be true for all \(\rho \). However, we should be careful, as unlike complex matrices, quaternionic matrices do not necessarily commute when they are diagonal (because scalar quaternions do not in general commute), and so we cannot automatically conclude that diagonal quaternionic matrices will satisfy this requirement. However, we can use the quaternionic spectral theorem to find a basis where all \(Z_j\) are real and diagonal. In this basis the diagonality of S is sufficient to ensure that it can commute with \(Z_i\) (because \(ah = ha\) for \(a\in \mathcal {R}\), \(h\in \mathbb {H}\)). Hence, we can choose an diagonal matrix of quaternions for S, which in order to satisfy \(S^\ddag S = \mathbb {1}\) must be of the form \(\bigoplus \mathrm {Sp}\left( 1\right) \) (i.e. each diagonal element is a unit quaternion). \(\square \)
For the discussion in this text, we do not need to claim this is the most general quaternionic phase operation (although it may be so). However, we will show that within this particular group, we can still find non-trivial subgroups of branch local operations.
Lemma 4
An operation that induces an element of \(\mathrm {Sp}\left( 1\right) \) on a branch j, and does not change the other branches except by a global phase of \(Z_2\) is consistent with branch locality as applied to branch j.
Proof
The proof is similar to the case with complex quantum theory. For S to be local to branch j with associated measurement effect \(Z_j\), then any state where \({{\mathrm{tr}}}\left( Z_j \rho \right) = 0\) must not be changed. For simplicity, we shall use a basis where \(Z_j\) is real and diagonal (as is allowed by the spectral theorem).
The density matrix of states with no support in branch j has element \(\rho _{jj}=0\). We can argue that this means all other elements in row j and column j must be 0, using similar logic as holds in the usual quantum case: Pure states in quaternionic quantum theory are rank-1 projectors (Lemma 3.1.1 in [48]), which may be written \(|\phi \rangle \langle \phi |\) (for quaternionic bras and kets); and so any pure state with no support in branch j will have \(\phi _j = 0\); and as 0 conjugates to itself, this means that the entire row j and column j in the matrix are 0. As mercifully \(h h^\ddag \ge 0\) for \(h \in \mathbb {H}\), if a state has no support for branch j, then every pure state it is composed from (which is always possible according to the spectral theorem) must have no support for branch j. Each of these will also only have 0s in row j and column j, and so all of these elements in \(\rho \) will be 0.
When S is a diagonal matrix where every diagonal element is 1 except for \(S_{jj}\), branch locality will therefore automatically be respected for density matrices with 0s in row j and column j. Hence, we can associate this choice of \(S\in \mathrm {Sp}\left( 1\right) \) with that branch.
Unlike with quantum theory, the global phase freedom for quaternions cannot be the same \(\mathrm {Sp}\left( 1\right) \) phase freedom available to each branch: for \(h \in \mathrm {Sp}\left( 1\right) \), application of the global phase \(G = {{\mathrm{diag}}}\left( h, \ldots h\right) \) gives \(G \rho G^\ddag = h \rho h^\ddag \), which amounts to conjugating every element in \(\rho \) with h. Because quaternions do not commute, in general this will have a non-trivial effect on \(\rho \) (even if h is restricted to a complex number). Only the real elements of \(\mathrm {Sp}\left( 1\right) \), which correspond to \(\{1, -\,1\} = Z_2\), commute and thus are never observable globally. Hence only \(Z_2\) can be taken as global phase operations which have no effect on any observable state (see also Lemma 33 and discussion in Appendix B of [13]). \(\square \)
This works to our advantage: unlike a complex global phase, a quaternionic global phase would cause us problems with commutativity: if two spatially disjoint agents could both act to span the entire phase-group of a quaternionic two-level system, then relativistic observers might disagree on what the resultant transformation should be, and this would ultimately conflict with the objective reality associated with probabilistic clicks in the detector [45]. Without a quaternionic global phase, branch locality can divide the quaternionic phase group up into subgroups, each of which with elements that commute with all elements in the other subgroups. (The \(N=2\) case is discussed in [45], where the two phase groups end up corresponding to the left and right isoclinic rotations in \(\mathrm {SO}\left( 4\right) \), and the only shared element other than identity corresponds to the inversion \(1\rightarrow -\,1\), which is what we require for our interferometric computation.)
Rights and permissions
About this article
Cite this article
Garner, A.J.P. Interferometric Computation Beyond Quantum Theory. Found Phys 48, 886–909 (2018). https://doi.org/10.1007/s10701-018-0142-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10701-018-0142-7




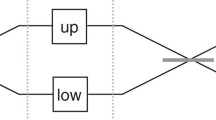
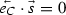 . This can be conceptually understood by discarding half of the branches and performing interferometry on the remaining half: the choice of branches included in the subset in will general govern whether the subset is balanced, constant or neither, and if it was one of the first two, then a lower-dimension version of the algorithm should work on these. It would thus be disingenuous if all balanced functions resulted in the same statistics.
. This can be conceptually understood by discarding half of the branches and performing interferometry on the remaining half: the choice of branches included in the subset in will general govern whether the subset is balanced, constant or neither, and if it was one of the first two, then a lower-dimension version of the algorithm should work on these. It would thus be disingenuous if all balanced functions resulted in the same statistics.