Skip to main content
SpringerLink
Log in

Hubble Law: Measure and Interpretation

  • Published:
Foundations of Physics Aims and scope Submit manuscript

Abstract

We have had the chance to live through a fascinating revolution in measuring the fundamental empirical cosmological Hubble law. The key progress is analysed: (1) improvement of observational means (ground-based radio and optical observations, space missions); (2) understanding of the biases that affect both distant and local determinations of the Hubble constant; (3) new theoretical and observational results. These circumstances encourage us to take a critical look at some facts and ideas related to the cosmological red-shift. This is important because we are probably on the eve of a new understanding of our Universe, heralded by the need to interpret some cosmological key observations in terms of unknown processes and substances.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

Notes

  1. V may be replaced by \(c\,z\), where c is the velocity of light and z the so-called “red-shift”.

  2. Sosie is a French word for twins not genetically linked.

  3. Some objects may be excluded from the sample because of an incomplete set of data, as it will be seen for Cepheids.

  4. The letter \(\kappa \) refers to the absorption by ionized Helium.

  5. The incompleteness has complex origin for Cepheids because to be included in the sample both apparent magnitudes (e.g. V and I) must be observed during a full phase and this is affected by extinction and amplitude.

  6. Note that it would be possible to calculate the colour excess (and thus the intrinsic \((V-I)_0\)) if the PLC relation could be replaced by a PL relation. This can be done by writing two Eq. 6, in V and I, equating them and by extracting the colour excess.

References

  1. Slipher, V.M.: On spectrographic observations of nebulae and clusters. PAAS. 4, 284 (1922)

    Google Scholar 

  2. Lemaître, G.: Un univers homogène de masse constante et de rayon croissant rendant compte de la vitesse radiale des nébuleuses extragalactiques. AASB. 47, 49 (1927)

    MATH  Google Scholar 

  3. Lundmark, K.: The motions and distances of spiral nebulae. MNRAS 85, 865 (1925)

    Article  ADS  Google Scholar 

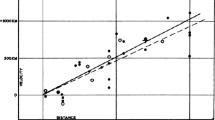
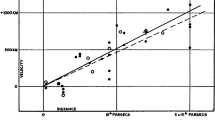
  4. Hubble, E.: A relation between distance and radial velocity among extragalactic nebulae. Proc. Nat. Acad. Sci. 15, 168–173 (1929)

    Article  ADS  MATH  Google Scholar 

  5. Maddox, J.: Dispute over scale of Universe. Nature 307, 313 (1984)

    Article  ADS  Google Scholar 

  6. Giovanelli, R.: Less expansion more agreement. Nature 400, 111–112 (1999)

    Article  ADS  Google Scholar 

  7. Roberts, M.S.: The neutral Hydrogen content of late-type spiral galaxies. Astron. J. 67, 437 (1962)

    Article  ADS  Google Scholar 

  8. Gouguenheim, L.: Neutral Hydrogen content of small galaxies. Astron. Astrophys. 3, 281 (1969)

    ADS  Google Scholar 

  9. Tully, R.B., Fisher, R.: A new method for determining distances to galaxies. Astron. Astrophys. 54, 661 (1977)

    ADS  Google Scholar 

  10. Teerikorpi, P.: Observational selection bias affecting the determination of the extragalactic distance scale. Ann. Rev. Astron. Astrophys. 35, 101–136 (1997)

    Article  ADS  Google Scholar 

  11. Teerikorpi, P.: The inverse Tully-Fisher relation. Astro Lett. and Comm. 31, 263 (1995)

    ADS  Google Scholar 

  12. Terry, J.N., Paturel, G., Ekholm, T.: Local velocity field from sosie galaxies : The Peeble’s model. Astron. Astrophys. 393, 57 (2002)

    Article  ADS  Google Scholar 

  13. Spaenhauer, A.M.: A systematic comparison of four methods to derive stellar space densities. Astron. Astrophys. 65, 313 (1978)

    ADS  Google Scholar 

  14. Bottinelli, L., Gouguenheim, L., Paturel, G., Teerikorpi, P.: The Malmquist bias and the value of \(H_0\) from the Tully-Fisher Relation. Astron. Astrophys. 156, 157 (1986)

    ADS  Google Scholar 

  15. Bottinelli, L., Gouguenheim, L., Paturel, G., Teerikorpi, P.: The Malmquist bias in the extragalactic distance scale : Controversies and misconceptions. Astrophys. J. 328, 4 (1988)

    Article  ADS  Google Scholar 

  16. Lutz, T.E., Kelker, D.H.: On the Use of Trigonometric Parallaxes for the Calibration of Luminosity Systems: Theory. PASP 85, 573 (1973)

    Article  ADS  Google Scholar 

  17. Feast, M.W., Catchpole, R.M.: The Cepheid period-luminosity zero-point from HIPPARCOS trigonometrical parallaxes. MNRAS 286, L1–L5 (1997)

    Article  ADS  Google Scholar 

  18. Freedman, W.L. et al., Final results from the Hubble Space Telescope Key Project to measure the Hubble constant. Astrophys.J 553, 47-72

  19. Beaton, R.L., Freedman, W.L., Madore, B.F., et al.: The Carnegie-Chicago Hubble Program I : A new approach to the distance ladder. Astrophys. J. 832, 2101 (2016)

    Article  Google Scholar 

  20. Teerikorpi, P.: Malmquist bias in a relation of the form \(M=a P+b\). Astron. Astrophys. 141, 407 (1984)

    ADS  Google Scholar 

  21. Hamuy, M., Phillips, M.M., Suntzeff, N.B.: et al, The Hubble diagram of the Calan/Tololo Type Ia Supernovae and the value of \(H_0\). Astron. J. 112, 2398 (1996)

    Article  ADS  Google Scholar 

  22. Riess, A.G., Filippenko, A.V., Challis, P., et al.: Observational evidence from supernovae for an acccelerating universe and a cosmological constant. Astron. J. 116, 1009 (1998)

    Article  ADS  Google Scholar 

  23. Perlmutter, S., Aldering, G., Goldhaber, G., et al.: Measurement of \(\Omega \) and \(\Lambda \) from 42 high-red-shift supernovae. Astrophys J. 517, 565 (1999)

    Article  ADS  Google Scholar 

  24. Bennett, C.L., Larson, D., Weiland, J.L., et al.: Nine-Year Wilkinson Microwave Anisotropy Probe (WMAP) observations : Final Maps and Results. Astrophys. J. Supl. 208, 20 (2013)

    Article  ADS  Google Scholar 

  25. Ade, P.A.R., Aghanin, N., Arnaud, M., et al.: Planck 2015 results. XIII. Cosmological parameters. Astron. Astrophys. 594, 15 (2016)

    Article  Google Scholar 

  26. Gieren, W., Fouqué, P., Gomez, M.: Cepheid period radius and period luminosity relations and the distance to the Large Magellanic Cloud. Astrophys. J. 496, 17 (1998)

    Article  ADS  Google Scholar 

  27. Benedict, G.F., Mc Arthur, B.E., Feast, M.W., et al.: Hubble space telescope fine guidance sensor parallaxes of Galactic Cepheid variable stars: period luminosity relation. Astron. J. 133, 1810 (2007)

    Article  ADS  Google Scholar 

  28. Herrnstein, J.R., Moran, J.M., Greenhill, L.J., et al.: A geometric distance to the galaxy NGC 4258 from orbital motions in a nuclear gas disk. Nature 400, 539 (1999)

    Article  ADS  Google Scholar 

  29. Hoffman, S.L., Riess, A.G., Macri, L.M., et al.: Optical identification of Cepheids in 19 host galaxies of Type Ia Supernovae and NGC 4258 with the Hubble space telescope. Astrophys. J. 830, 10 (2016)

    Article  ADS  Google Scholar 

  30. Riess, A.G., Macri, L.M., Hoffman, S.L., et al.: A 2.4% determination of the local value of the hubble constant. Astrophys. J. 826, 56 (2016)

    Article  ADS  Google Scholar 

  31. Tully, R.B., Courtois, H.M., Dolphin, A.E., et al.: Cosmicflow-2: data. Astron. J. 146, 86 (2013)

    Article  ADS  Google Scholar 

  32. Teerikorpi, P.: Cluster population incompleteness and distances from the TF relation—theory and numerical example. Astron. Astrophys. 173, 39 (1987)

    ADS  Google Scholar 

  33. Sandage, A.: Cepheids as distance indicators when used near their detection limit. PASP 100, 935 (1988)

    Article  ADS  Google Scholar 

  34. Schechter, P.L.: Mass-to-light ratios for Elliptical galaxies. Astron. J. 85, 801 (1980)

    Article  ADS  Google Scholar 

  35. Tully, R.B.: Origin of the Hubble constant controversy. Nature 334, 209 (1988)

    Article  ADS  Google Scholar 

  36. Teerikorpi, P., Ekholm, T., Hanski, M.O., Theureau, G.: Theoretical aspects of the inverse Tully–Fisher relation as a distance indicator: incompleteness in \(logV_{max}\), the relevant slope, and the calibrator sample bias. Astron. Astrophys. 343, 713 (1999)

    ADS  Google Scholar 

  37. Teerikorpi, P., Paturel, G.: Evidence for the extragalactic Cepheid distance bias from the kinematical distance scale. Astron. Astrophys. 381, L37–L40 (2002)

    Article  ADS  Google Scholar 

  38. Madore, B.F., in From the Realm of the Nebulae to Populations of Galaxies, Eds. D’Onofrio, M., Rampazzo, R., Zaggia, S., Springer, New York, pp. 132 (2016)

  39. Madore, B.F.: The period luminosity relation: IV—intrinsic relation and reddenings for the Large Magellanic Cloud Cepheids. Astrophys. J. 253, 575 (1982)

    Article  ADS  Google Scholar 

  40. Van den Bergh, S.: The galaxies of the local group. JRAS of Canada 62, 145 (1968)

    ADS  Google Scholar 

  41. Inno, L., Bono, G., Matsunaga, N.: The panchromatic view of the Magellanic Cloud from classical Cepheids I: distance, rddening and geometry. Astrophys. J. 832, 176 (2016)

    Article  ADS  Google Scholar 

  42. Ekholm, T., Lanoix, P., Teerikorpi, P., et al.: Investigation of the local supercluster velocity field. Astron. Astrophys. 351, 827–833 (1999)

    ADS  Google Scholar 

  43. Ekholm, T., Baryshev, Y., Teerikorpi, P., et al.: On the quiescence of the Hubble flow in the vicinity of the Local Group: A study using galaxies with distances from the Cepheid PL-relation. Astron. Astrophys. 368, L17–L20 (2001)

    Article  ADS  Google Scholar 

  44. Karachentsev, I.D., et al.: The very local Hubble flow. Astron. Astrophys. 389, 812–824 (2002)

    Article  ADS  Google Scholar 

  45. Sandage, A.: The red-shift-distance relation. IX. Astrophys. J. 307, 1 (1986)

    Article  ADS  Google Scholar 

  46. Paturel, G., Teerikorpi, P.: The extragalactic Cepheid bias: a new test using the Period–Luminosity–color relation. Astron. Astrophys 452, 423–430 (2006)

    Article  ADS  Google Scholar 

  47. Lanoix, P., Garnier, R., Paturel, G., et al.: Extragalactic Cepheid database. Astron. Nachr. 320, 1 (1999)

    Article  ADS  Google Scholar 

  48. Baryshev, Yu., Teerikorpi, P.: Fundamental Questions of Practical Cosmology. Springer, Berlin (2012)

    Book  Google Scholar 

  49. Baryshev, Y.V.: Paradoxes of the cosmological physics in the beginning of the 21-th century. In: Particle and Astroparticle Physics, Gravitation and Cosmology: Predictions, Observations and New Projects, pp. 297–307 (2015). arXiv:1501.01919

  50. Harrison, E.R.: The red-shift-distance and velocity-distance laws. Astrophys. J. 403, 28 (1993)

    Article  ADS  Google Scholar 

  51. Sanejouand, Y.H.: A simple Hubble like law in lieu of dark energy (2015). arXiv:1401.2919v6

  52. de Sitter, W.: On Einstein’s theory of gravitation and its astronomical consequences. In: MNRAS. LXXVI. 9, 699 (1916)

  53. de Sitter, W.: On Einstein’s theory of gravitation and its astronomical consequences II. In: MNRAS LXXVII. 2, 155 (1917)

  54. de Sitter, W.: On Einstein’s theory of gravitation and its astronomical consequences III. In: MNRAS LXXVIII. 1, 3 (1917)

  55. Eddington, A.S.: The Mathematical Theory of Relativity, p. 161. Cambridge University Press, Cambridge (1923)

    MATH  Google Scholar 

  56. Tolman, R.C.: On the astronomical implications of the de Sitter line element of the universe. Astrophys. J. 69(245), 1929 (1929)

    Google Scholar 

  57. Sandage, A.: Galaxies and the Universe. The University of Chicago Press, Chicago (1975)

    Google Scholar 

  58. Sandage, A.: Astronomical problems for the next three decades. In: Mamaso, A., Munch, G. (eds.) Key Problems in Astronomy and Astrophysics. Cambridge University Press, Cambridge (1995)

    Google Scholar 

  59. Sandage, A.: The Tolman surface brightness test for the reality of the expansion, V. Provenance of the test and a new representation of the data for three remote Hubble space telescope galaxy clusters. Astron. J. 139, 728 (2010)

    Article  ADS  Google Scholar 

  60. Sandage, A.: The change of red-shift and apparent luminosity of galaxies due to the deceleration of the expanding universes. ApJ 136, 319 (1962)

    Article  ADS  Google Scholar 

  61. Liske, J., Grazian, A., Vanzella, E., et al.: Cosmic dynamics in the era of extremely large telescopes. Mon. Not. R. Astron. Soc. 386, 1192 (2008)

    Article  ADS  Google Scholar 

  62. Baryshev, Y.V.: The hierarchical structure of metagalaxy a review of problems, Reports of Special Astrophysical Observatory of the Russian Academy of Sciences 14, p. 24 (1981) (English translation: 1984 Allerton Press)

  63. Baryshev, Y.V.: Field fractal cosmological model as an example of practical cosmology approach, in Practical Cosmology, Proceedings of the International Conference held at Russian Geographical Society, 23-27 June, 2008, Vol. 2, p. 60 (2008). arXiv:0810.0162

  64. Lopez-Corredoira, M.: Tests of the expansion of the Universe (2015). arXiv:1501.01487

  65. Sandage, A., Reindl, B., Tammann, G.: The linearity of the cosmic expansion field from 300 to 30,000 km s-1 and the bulk motion of the local supercluster with respect to the cosmic microwave background. Astrophys. J. 714, 1441 (2010)

    Article  ADS  Google Scholar 

  66. Teerikorpi, P., Hanski, M., Theureau, G., et al.: The radial space distribution of KLUN-galaxies up to 200 Mpc: incompleteness or evidence for the behavior predicted by fractal dimension 2? Astron. Astrophys. 334, 395 (1998)

    ADS  Google Scholar 

  67. Sylos Labini, F.: Inhomogeneous universe. Class. Quant. Grav. 28, 4003 (2011)

  68. Tekhanovich, D.I., Baryshev, Y.V.: Global Structure of the Local Universe according to 2MRS Survey; ISSN 1990-3413, Astrophys. Bull., vol. 71, No. 2, pp. 155–164 (2016). arXiv: 1610.05206

  69. Baryshev, Y.V.: Two fundamental cosmological laws of the Local Universe, Proceedings of the International Conference, Cosmology On Small Scales, Local Hubble Expansion and Selected Controversies in Cosmology, Prague, September 2124, 2016, Edited by Krǐzek, M., Dumin, Y.V.: Institute of Mathematics, Czech Academy of Sciences, Prague, pp. 9 22 (2016) arXiv:1610.05943

  70. Wiens, E., Nevsky, A.Yu., Schiller, S.: Resonator with ultra-high stability as a probe for equivalence-principle-violating physics (2016). arXiv: 1612.01467V1

  71. Landau, L.D, Lifschitz, E.M.: Theory of fields, Mir Ed., Moscow (1970)

  72. Kopeikin, S.: Celestial Ephemerides in an expanding universe. Phys. Rev. D 86, 064004 (2012)

    Article  ADS  Google Scholar 

  73. Kopeikin S.: Local gravitational physics of the Hubble expansion, Eur. Phys. J. Plus 130, p. 11 (2015). arXiv:1407.6667

  74. Zwicky, F.: On the masses of nebulae and of clusters of nebulae. Astrophys. J. 86, 217 (1937)

    Article  ADS  MATH  Google Scholar 

  75. Milgrom, M.: A modification of the Newtonian dynamics as a possible alternative to the hidden mass hypothesis. Astrophys. J. 270, 365 (1983)

    Article  ADS  Google Scholar 

  76. Bekenstein, J.: Relativistic gravitation theory for the modified Newtonian dynamics paradigm. Phys. Rev. D70, 083509 (2004)

    ADS  Google Scholar 

  77. Blanchet, L.: Gravitational polarization and the phenomenology of MOND. Class. Quant. Gravity 24, 3529 (2007)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  78. Guth, A.H.: Inflationary universe: a possible solution to the horizon and flatness problem. Phys. Rev. D 23, 347 (1981)

    Article  ADS  Google Scholar 

  79. Peebles, P.J.E.: Principles of Physical Cosmology. Princeton University Press, Princeton (1993)

    Google Scholar 

Download references

Acknowledgements

Y.B. thanks for support from the Saint-Petersburg State University research Project No. 6.38.18.2014. We are very grateful to our collaborators over many years Lucienne Gouguenheim, Gilles Theureau, Jean-Noël Terry, Chantal Petit and Mikko Hanski, and remember with admiration the late Lucette Bottinelli and Timo Ekholm. We want to sincerely thank referees for their valuable contributions.

Author information

Authors and Affiliations

  1. Observatoire de Lyon, Retired from Universite Claude-Bernard, 69230, Saint-Genis Laval, France

    Georges Paturel

  2. Department of Physics and Astronomy, Tuorla Observatory, University of Turku, 21500, Piikkiö, Finland

    Pekka Teerikorpi

  3. Department of Astronomy, St. Petersburg State University, Staryj Peterhoff, St.Petersburg, Russia, 198504

    Yurij Baryshev

Authors
  1. Georges Paturel
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Pekka Teerikorpi
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Yurij Baryshev
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Georges Paturel.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Paturel, G., Teerikorpi, P. & Baryshev, Y. Hubble Law: Measure and Interpretation. Found Phys 47, 1208–1228 (2017). https://doi.org/10.1007/s10701-017-0093-4

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10701-017-0093-4

Keywords

Search

Navigation