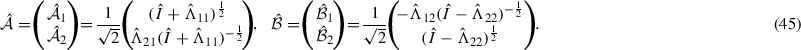Abstract
The presented enhanced version of Eriksen’s theorem defines an universal transform of the Foldy–Wouthuysen type and in any external static electromagnetic field (ESEMF) reveals a discrete symmetry of Dirac’s equation (DE), responsible for existence of a highly influential conserved quantum number—the charge index distinguishing two branches of DE spectrum. It launches the charge-index formalism (CIF) obeying the charge-index conservation law (CICL). Via its unique ability to manipulate each spectrum branch independently, the CIF creates a perfect charge-symmetric architecture of Dirac’s quantum mechanics (DQM), which resolves all the riddles of the standard DE theory (SDET). Besides the abstract CIF algebra, the paper discusses: (1) the novel accurate charge-symmetric definition of the electric-current density; (2) DE in the true-particle representation, where electrons and positrons coexist on equal footing; (3) flawless “natural” scheme of second quantization; and (4) new physical grounds for the Fermi–Dirac statistics. As a fundamental quantum law, the CICL originates from the kinetic-energy sign conservation and leads to a novel single-particle physics in strong-field situations. Prohibiting Klein’s tunneling (KT) in Klein’s zone via the CICL, the precise CIF algebra defines a new class of weakly singular DE solutions, strictly confined in the coordinate space and experiencing the total reflection from the potential barrier.
Similar content being viewed by others
Notes
Published as far back as 1930, the qualitative argumentation of Landau and Peierls up to now remains very influential. It is presented on the first pages of [2], as one of the constitutive ideas of this famous book on QED.
In the recent work by Silenko [8] the primary Eriksen transform is supposed to be applicable in any external EM field. In a strong static field this idea contradicts to arguments of Eriksen, who noted in [7] that the existence of zero eigenvalues of DH leads to a mathematical singularity which destroys the consistency (one-to-one mapping) of the transform—it can be easily illustrated by example of a constant potential energy, whose value exceeds \(mc^2\). Just this reasoning has led us to a conclusion that the enhanced Eriksen transform must use the kinetic-energy operator instead of the full Hamiltonian. On the other hand, if there is no inertial reference frame, where the external field is time-independent, then a formal block-diagonalization becomes meaningless—a time-dependent transform in general case leads to two interconnected Pauli-type equations.
Sometimes we shall call it the formalism of paulions.
One can guess from the structure of the paulionic Hamiltonian (see, e.g., Sect. 7), that a paulion is an electron whose 2-component wave function is defined in terms of the electron center-of-mass coordinate and spin wrt the center of mass.
A deplorable result of the conventional second-quantization procedure is that the theory gets into a logically unacceptable situation, when the commutation relations between the creation and annihilation operators are of decisive importance for both the physical energy spectrum and charge density to such an extent that the single-particle physical meaning of the primary DE appears to be completely destroyed. The electron–positron vacuum appears in SDET as a “Dirac sea” (see, e.g., [10–14]), which possesses infinitely large amounts of energy and charge. In this situation a smooth return back to the initial wave equation, in case of a single particle seems impossible. This circumstance has created a widespread wrong opinion that “unlike the Schrödinger equation for a single particle, the Dirac theory in principle is a many-body theory”—the quote from [15], p. 15, which is consonant with the statement of [9], p. 22: “in the relativistic case it is impossible\(\ldots \) to construct a consistent single-particle theory”. A reason of all SDET difficulties and delusions was the absence of the knowledge about the quantum charge-index. The obvious inequality of rights of electrons and positrons in the SDET, where real positrons appear as a result of second quantization, stimulated Santilli [16] to propose an isodual theory of antimatter, which, in author’s opinion, describes matter and antimatter on equal footing. Santilli’s theory, however, doesn’t contain anything resembling the charge-index observable, so the isodual mapping (of matter- and antimatter worlds on each other) per se is unable to resolve the problem of correct electric-current definition, whereas the quantum charge-index operator does it in a natural charge-symmetric manner (Sect. 9).
That was another reason for the wrong belief that DE has a many-body nature, which supposedly might manifest itself in strong-field situations.
In nonrelativistic QM it is a very specific feature which is implemented only in a potential well with infinitely high walls. For DQM in Klein’s zone such a behavior of wave functions is standard as the CICL forbids changing the KES. This fact means a strict spacial confinement of Dirac’s particle by the respective charge-index alteration surface in Klein’s zone.
The CIF algebra provides a strict upholding of the orthonormality relations, embracing the new discontinuous solutions. This immediately follows from the continuity equations for products \(\psi ^\dag _1(\varvec{r},t)\psi ^{\phantom {\dag }}_2(\varvec{r},t)\), where the multipliers are regarded as generalized functions.
Eriksen [7] defines the \(-\frac{1}{2}\) root operator in (11) via the binomial expansion in powers of \(\frac{1}{4}(\hat{\beta }\hat{\lambda }+\hat{\lambda }\hat{\beta }-2\hat{I}_4)\) in view of \(2\hat{I}_4+\hat{\beta }\hat{\lambda }+\hat{\lambda }\hat{\beta }=4\,[\hat{I}_4+\frac{1}{4}(\hat{\beta }\hat{\lambda }+\hat{\lambda }\hat{\beta }-2\hat{I}_4)]\). The notation of \(\hat{G}\) in the form of a quotient means that the numerator and denominator in (11) are commuting.
For example, operator \(\big (\hat{\mathcal {H}}_\mathrm{kin}^2\big )^{-\frac{1}{2}}\) can be represented by the binomial expansion
$$\begin{aligned} \big (\hat{\mathcal {H}}_\mathrm{kin}^2\big )^{-\frac{1}{2}}= \mathcal {E}_0^{-1}\sum \limits _{n=0}^\infty \left( \begin{array}{c} \!-\frac{1}{2}\\ n \end{array}\right) \! \bigg (\frac{\hat{\mathcal {H}}_\mathrm{kin}^2}{\mathcal {E}_0^2}-\hat{I}_4\!\bigg )^{\!n}, \end{aligned}$$(19)with \(\mathcal {E}_0\) being a positive number. Operating on an arbitrary function \(\psi \), this expansion will produce convergent results provided that all the kinetic energies \(\mathcal {E}_\mathrm{kin}=\mathcal {E}-e\varPhi (\varvec{r})\) in the spectrum of \(\psi \) satisfy the condition \(0<|\mathcal {E}_\mathrm{kin}|<\mathcal {E}_0\sqrt{2}\).
This explains why these functions are obliged to be discontinuous at the charge-index alteration surface—otherwise, according to the unicity theorem of the partial-differential-equation theory, they would be identically equal to zero in the whole coordinate space.
Spatial continuity is supposed to be a natural mathematical property of eigenfunctions of the paulionic Hamiltonians.
In the standard representation, as it was discussed at the end of Sect. 2, the corresponding functions \(\psi ^\mathrm{a}_\mathcal {E}=\psi _{\mathcal {E},\lambda _+}\!\!\) and \(\psi ^\mathrm{b}_\mathcal {E}=\psi _{\mathcal {E},\lambda _-}\!\!\) must possess weak singularities at the surface \(S(\mathcal {E})\). The required jumps of \(\psi ^\mathrm{a}_\mathcal {E}\) and \(\psi ^\mathrm{b}_\mathcal {E}\) appear in a natural manner as a result of action of the bare momentum operator \(\varvec{\hat{p}}\), contained in the \(2{\times }2\) off-diagonal elements of \(\hat{G}^\dag \!\), on functions \(\phi ^\mathrm{a}_\mathcal {E}\) and \(\phi ^\mathrm{b}_\mathcal {E}\), which have discontinuous normal derivatives at \(S(\mathcal {E})\).
Just this circumstance allows us to conclude that the real electrons and positrons are the states of the same sophisticated Hamiltonian and have to be considered as identical particles obeying the quantum-mechanical indistinguishability principle.
In terms of Sect. 3
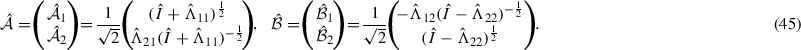
It should be remembered that the product of two matrices of dimensions \(l \times m\) and \(m\times n\) is an \(l \times n\) matrix.
Our theory, in some its part, appears to be formally consonant with the recent nilpotent considerations by Rowlands [31]. However, the strict isolation of the observable and unobservable spaces of DE makes us suspect the statement of [31], p. 36: “\(\ldots \) some of the properties fermions are known to possess (in particular, spin \(^1\!\!/\!_2\)) could be explained by imagining a fermion to exist simultaneously in two spaces, one of which is recognizable as ‘real space’\(\ldots \) and the other can be seen as a ‘vacuum space’, which remains unobservable”.
It is worth noting here that decomposition (59), formally applied to an unacceptable continuous \(\psi \)-function, containing KT in the SDET, would lead to an inadmissible fact, incompatible with the fundamental quantum-mechanical principle of superposition [12], that each of the arising functions \(\psi ^\mathrm{a}\) and \(\psi ^\mathrm{b}\), individually, could not be a solution of DE in view of discontinuity of respective flux density vectors. This contradiction, indicated for the first time in [1], is a substantial argument in favor of the advanced DE mathematics in strong fields, which strictly adheres to the principle of superposition for states with different quantum charge-index numbers.
Nonlocality of an operator means its dependence upon the spatial derivatives of all orders.
Since the spin energy in a magnetic field is a constituent of kinetic energy, which cannot be less than \(mc^2\), the expectation value of the difference \(\hat{\varepsilon }^{\,2}\!-|ec\hslash H|\) is always \(\ge m^2c^4\), regardless of how big is the field strength H.
The bispinor true-particle representation for the universal electron–positron \(\psi \)-function can be constructed by analogy with (51) via the former transformation matrix \(\hat{G}\):
$$\begin{aligned} \psi _\mathrm{u}\!=\hat{G}^\dag \psi ^\mathrm{o}_\mathrm{u},\quad \hat{\mathcal {H}}_\mathrm{u}\!=\hat{G}^\dag \hat{\mathcal {H}}^\mathrm{o}_\mathrm{u}\hat{G}=\hat{\mathcal {A}}\hat{K}^\mathrm{a}\hat{\mathcal {A}}^\dag \! +\hat{\mathcal {B}}\widetilde{K}^\mathrm{b}\hat{\mathcal {B}}^\dag . \end{aligned}$$(79)The charge-index operator retains here its former form (55) and the role of a quantum tool distinguishing between electrons and positrons, which are described now by orthogonal bispinors and presented on equal footing—see equation (130) of “Appendix”. We prefer the true-paulion representation (77) in view of its terseness.
As a matter of fact, the standard Lagrangian, used in the SDET (see, e.g., [33]), implements a defective least-action principle, which is unable to ensure the stability of the quantum system wrt small perturbations caused by the \(\gamma \)-quantum emission processes. In the SDET the necessary stability is achieved via a forced filling of the negative-energy states, which forms the infinite Dirac sea and incredibly falsifies the structure of the quantum world of electrons and positrons.
Along with orthogonality of \(\psi ^\mathrm{a}\) and \(\psi ^\mathrm{b}\) in (86), (87) we are using the obvious chain of equalities \(\psi ^{\mathrm{b}\dag }\psi ^\mathrm{b}\!=\psi ^\mathrm{T}_\mathrm{p}\hat{\gamma }^\dag _2\hat{\gamma }^{\phantom {\dag }}_2\psi ^*_\mathrm{p}\!=(\psi ^\dag _\mathrm{p}\psi ^{\phantom {\dag }}_\mathrm{p})^\mathrm{T}\!\! =\psi ^\dag _\mathrm{p}\psi ^{\phantom {\dag }}_\mathrm{p}\), where, as usual, the symbol \(\mathrm{T}\) denotes transposed matrices.
Symmetry of expressions (98), (101) wrt replacing \(\psi ^{\phantom {\dag }}_\mathrm{e}\!\rightleftarrows \psi ^{\phantom {\dag }}_\mathrm{p}\) is ensured by their transpose invariance, which is easily verified via the relations: \(\hat{\gamma }^\mathrm{T}_2\!=\hat{\gamma }^{\phantom {\dag }}_2\!=-\hat{\gamma }^*_2,\; (\hat{\gamma }^{\phantom {\dag }}_2\varvec{\hat{\alpha }}) {^\mathrm{T}}\!=-\hat{\gamma }^{\phantom {\dag }}_2\varvec{\hat{\alpha }}\).
In (118) we have used the relations \(\hat{\gamma }^{\phantom {\dag }}_2\hat{\pi }{^*}=-\hat{\pi }\hat{\gamma }^{\phantom {\dag }}_2\), where \(\hat{\pi } =\hat{\beta }, \varvec{\hat{\alpha }}, \hat{\mathcal {H}}_\mu , \hat{\mathcal {H}}_\delta \). The replacement \({e\rightarrow -e}\) in (6) does not affect the constants \(\mu _\mathrm{a}\) and \(\delta _\mathrm{a}\), which means that the both anomalous moments change their signs.
As usual, we define the charge-conjugation transform with accuracy to an insignificant constant factor \(f:\;\;|f|=1\).
References
Kononets, Y.V.: Charge conservation, Klein’s paradox and the concept of paulions in the Dirac electron theory: new results for the Dirac equation in external fields. Found. Phys. 40, 545–572 (2010)
Berestetskii, V.B., Lifshitz, E.M., Pitaevskii, L.P.: Quantum Electrodynamics. Pergamon, Oxford (1982)
Foldy, L.L., Wouthuysen, S.A.: On the Dirac theory of spin 1/2 particles and its non-relativistic limit. Phys. Rev. 78, 29–36 (1950)
Thaller, B.: The Dirac Equation. Springer, Berlin (1992)
Brouder, Ch., Alouani, M., Bennemann, K.H.: Multiple-scattering theory of x-ray magnetic circular dichroism: implementation and results for the iron K edge. Phys. Rev. B 54, 7334–7349 (1996)
Case, K.M.: Some generalizations of the Foldy–Wouthuysen transformation. Phys. Rev. 95, 1323–1328 (1954)
Eriksen, E.: Foldy–Wouthuysen transformation. Exact solution with generalization to the two-particle problem. Phys. Rev. 111, 1011–1016 (1958)
Silenko, A.J.: General method of the relativistic Foldy–Wouthuysen transformation and proof of validity of the Foldy–Wouthuysen Hamiltonian. Phys. Rev. A 91, 022103–022108 (2015)
Akhiezer, A.I., Berestetskii, V.B.: Quantum Electrodynamics, 4th edn. Nauka, Moscow (1981). (in Russian)
Grant, I.P.: Relativistic Quantum Theory of Atoms and Molecules: Theory and Computation. Springer, New York (2007)
Wachter, A.: Relativistic Quantum Mechanics. Springer, New York (2011)
Dirac, P.A.M.: The Principles of Quantum Mechanics, 4th edn. Clarendon, Oxford (1959)
Pauli, W.: General Principles of Quantum Mechanics. Springer, Berlin (1980)
Milonni, P.W.: The Quantum Vacuum: An Introduction to Quantum Electrodynamics. Academic Press, San Diego (1994)
Shen, S.-Q.: Topological Insulators: Dirac Equation in Condensed Matters. Springer, Berlin (2012)
Santilli, R.M.: Isodual Theory of Antimatter with applications to Antigravity, Grand Unification and Cosmology. Springer, Amsterdam (2006)
Klein, O.: Die Reflexion von Elektronen an einem Potentialsprung nach der relativistischen Dynamik von Dirac. Z. Phys. 53, 157–165 (1929)
Sauter, F.: Über das Verhalten eines Elektrons im homogenen elektrischen Feld nach der relativistischen Theorie Diracs. Z. Phys. 69, 742–764 (1931)
Sauter, F.: Zum “Kleinschen Paradoxon”. Z. Phys. 73, 547–552 (1932)
Flügge, S.: Practical Quantum Mechanics, vol. II. Springer, Berlin (1999)
Schwinger, J.: On gauge invariance and vacuum polarization. Phys. Rev. 82, 664–679 (1951)
Bjorken, J.D., Drell, S.D.: Relativistic Quantum Mechanics. McGraw-Hill, New York (1964)
Greiner, W., Müller, B., Rafelski, J.: Quantum Electrodynamics of Strong Fields. Springer, Berlin (1985)
Greiner, W.: Relativistic Quantum Mechanics: Wave Equations, 3rd edn. Springer, Berlin (2000)
Schwabl, F.: Advanced Quantum Mechanics, 4th edn. Springer, Berlin (2008)
Fradkin, E.S., Gitman, D.M., Shvartsman, S.M.: Quantum Electrodynamics: With Unstable Vacuum. Springer, Berlin (2011)
Bagrov, V.G., Gitman, D.: The Dirac Equation and Its Solutions. De Gruyter, Berlin (2014)
Chuprikov, N.L.: The stationary Dirac equation as a generalized Pauli equation for two quasiparticles. Found. Phys. 45, 644–656 (2015)
Strichartz, R.S.: A Guide to Distribution Theory and Fourier Transforms. CRC Press, Boca Raton (1994)
Blanchard, P., Brüning, E.: Mathematical Methods in Physics: Distributions, Hilbert Space Operators, and Variational Methods. Birkhäuser, Boston (2003)
Rowlands, P.: Space and antispace. In: Amoroso, R.L., Kauffman, L.H., Rowlands, P. (eds.) The Physics of Reality: Space, Time, Matter, Cosmos, pp. 29–37. World Scientific, Singapore (2013)
Kononets, Yu.V.: Relativistic analogue of the Pauli equation and Dirac electron states in strong magnetic fields. Europhys. Lett. 71, 517–523 (2005)
Toms, D.J.: The Schwinger Action Principle and Effective Action. Cambridge University Press, Cambridge (2007)
Stewart, I.: Why Beauty Is Truth: A History of Symmetry, pp. 277–278. Basic Books, New York (2008)
Dyson, F.J.: Innovation in physics. Sci. Am. 199(3), 74–82 (1958)
Acknowledgments
The author is grateful to his colleagues from the Condensed-Matter Theory Laboratory at the Kurchatov Institute, with special thanks to Yu. Kagan, L.A. Maksimov and L.B. Dubovskii, for their deep interest, objective scientific appraisal, and stimulating discussions of novel results presented in the paper. The work was partly supported by the Grants RFBR-13-02-00469 (Russian Foundation for Basic Research) and NS-4263.2014.2 (Programme of the President of Russia for the state support of leading scientific schools).
Author information
Authors and Affiliations
Corresponding author
Appendix: The Charge-Conjugation Transform and True Positron States
Appendix: The Charge-Conjugation Transform and True Positron States
Let us consider the function \(\widetilde{\psi }\) which satisfies DE with the reversed sign of e:
Taking into account the relationsFootnote 27
we easily get the well known charge-conjugation transform \(\hat{C}\) [2, 11] connecting \(\widetilde{\psi }\) with a solution \(\psi \) of the initial DE:Footnote 28
By analogy with Sect. 5, consider the collection of operators arising in the block-diagonalization of Hamiltonian \(\widetilde{\mathcal {H}}\):
Superscripts “\(\mathrm{a}\)” and “\(\mathrm{b}\)” here, as before, refer to physical and nonphysical states, respectively, of Hamiltonian \(\widetilde{\mathcal {H}}\). It seems evident that the charge-conjugation transform (119), applied to nonphysical states of Hamiltonian \(\hat{\mathcal {H}}\), generates the physical states of Hamiltonian \(\widetilde{\mathcal {H}}\). Similarly, the nonphysical states of \(\widetilde{\mathcal {H}}\) are the charge-conjugate physical states of \(\hat{\mathcal {H}}\).
Inserting \(\hat{\mathcal {H}}=\hat{G}^\dag \hat{\mathcal {H}}^\mathrm{o}\hat{G}\) into \(\widetilde{\mathcal {H}}=\hat{\gamma }^{\phantom {\dag }}_2\hat{\mathcal {H}}^*\hat{\gamma }^{\phantom {\dag }}_2\), one can easily obtain
where the block-diagonalizing unitary matrix \(\widetilde{G}\) for Hamiltonian \(\widetilde{\mathcal {H}}\) is defined via \(\hat{G}\) (44) as
As usual, the superscript \(\mathrm{T}\) designates transposed matrices.
In accordance with (44), the operators \(\widetilde{\mathcal {A}}\) and \(\widetilde{\mathcal {B}}\), implementing the block-diagonalization of \(\widetilde{\mathcal {H}}\), can be found immediately from the relation
As a result, we get:
It is obvious that the respective \(\phi \)-functions
satisfy the equations
with the eigenvalues \(\widetilde{\mathcal {E}}^\mathrm{a}\), \(\widetilde{\mathcal {E}}^\mathrm{b}\) being equal to the respective energies, with opposite sign, of states \(\phi ^\mathrm{b}\) and \(\phi ^\mathrm{a}\), whose complex conjugate counterparts stand in (125):
Summarizing the above considerations, we come to the exact charge-conjugation symmetry relations, connecting physical states of Hamiltonians \(\widetilde{\mathcal {H}}\) and \(\hat{\mathcal {H}}\) with respective nonphysical ones of \(\hat{\mathcal {H}}\) and \(\widetilde{\mathcal {H}}\), and vice versa:
As a general result, we can see from (120), (128) an exact relation between paulionic (\(\hat{K}^\mathrm{a}\)) and pseudo-antipaulionic (\(\hat{K}^\mathrm{b}\)) Hamiltonians, first published in [1]:
The functions \(\widetilde{\psi }^\mathrm{a}\) and \(\widetilde{\phi }^\mathrm{a}\) in the above must be regarded as physical wave functions of positrons and antipaulions, respectively, whose energy spectra coincide and tend to \(+\infty \) with increasing momentum. Simultaneously, \(\widetilde{\psi }^\mathrm{b}\) and \(\widetilde{\phi }^\mathrm{b}\) must be treated as nonphysical (unobservable) states of pseudo-electrons and pseudo-paulions, respectively, because their coincident energy spectra extend to \(-\infty \). The general relations (128) are, naturally, in full agreement with definitions of electronic and positronic \(\psi \)-functions in the SDET [2, 11].
In the free space one easily notices that, for a given momentum, an electronic state, as a physical solution of the primary DE, is described by exactly the same \(\psi \)-function as the positronic state with the mentioned momentum. This fact reflects the general specific feature of the SDET, that physical states with different electric charges here are not orthogonal. Just this circumstance makes the SDET operate with the orthonormal system of eigenstates of the primary DE, a half of which are not realized in nature in their original form. The complete wreck of the STED inevitably happens in strong fields, where the theory is unable to correctly define observable and unobservable states of Dirac’s particle.
The advanced theory exploits the mathematical apparatus (see Sect. 8), in which the physically observable electronic and positronic states are described by orthonormalized wave functions. In the bispinor true-particle representation (see equation (79)) one can see that the subsystem of positronic functions is connected with its standard representation via a simple unitary transform:
which confirms equal rights of electrons and positrons in the true-particle representation.
Rights and permissions
About this article
Cite this article
Kononets, Y.V. Novel Principles and the Charge-Symmetric Design of Dirac’s Quantum Mechanics: I. Enhanced Eriksen’s Theorem and the Universal Charge-Index Formalism for Dirac’s Equation in (Strong) External Static Fields. Found Phys 46, 1598–1633 (2016). https://doi.org/10.1007/s10701-016-0033-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10701-016-0033-8