Part feeding at high-variant mixed-model assembly lines

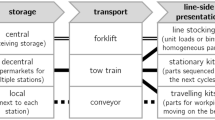
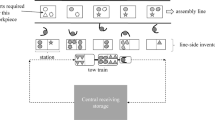
Abstract

The part feeding problem at automotive assembly plants deals with the timely supply of parts to the designated stations at the assembly line. According to the just-in-time principle, buffer storages at the line are frequently refilled with parts retrieved from a central storage area. In the industrial application at hand, this is accomplished by means of an internal shuttle system which supplies the various stations with the needed parts based on a given assembly sequence. The main objective is to minimize the required number of shuttle drivers. To solve this in-house transportation problem, a heuristic solution procedure is developed which is based on the decomposition of the entire planning problem into two stages. First, transportation orders are derived from the given assembly sequence. In the second stage, these orders are assigned to tours of the shuttle system taking transportation capacity restrictions, due dates and tour scheduling constraints into account. Numerical results show that the proposed heuristic solves even large-sized problem instances in short computational time. Benchmark comparisons with Kanban systems reveal the superiority of the proposed predictive part feeding approach.

Appendix: Mixed-integer liner optimization model

Sets

S :

The set of stations at the assembly line

M :

The set of parts

N :

The set of transportation orders including two dummy orders representing the start and end order of a tour

P :

The set of predefined paths through the plant

D :

The set of drivers

T :

The set of possible tours of a shuttle with $T: = \left\{ {0, \cdots ,t^{\max } } \right\}$ including dummy tour 0

$N^{Del} \subseteq N$ :

The set of real transportation orders

$N^{ms} \subseteq N$ :

The set of transportation orders delivering part $m \in M$ to station $s \in S$

$N^{p} \subseteq N$ :

The set of transportation orders which can be delivered on path $p \in P$

$M^{s} \subseteq M$ :

The set of parts assembled at station $s \in S$

$L^{ms} \subseteq L$ :

The set of part-specific bins which are used to transport part $m \in M$ to station $s \in S$

Q ^ms :

The set of accumulated part-specific bins of part $m \in M$ at station $s \in S$

$T^{real} \subseteq T$ :

The set of real tours with $T = T{}^{real} \cup \left\{ 0 \right\}$

Parameters

pt _n :

The processing time of transportation order $n \in N$

dd _n :

The due date of transportation order $n \in N$

w _n :

The width of one part-specific bin of transportation order $n \in N$

s _n :

The respective station of transportation order $n \in N$

conn ^D :

The time needed to connect and disconnect a trailer to and from the shuttle

capa ^D :

The available width of a shuttle

$tt_{{ps_{1} s_{2} }}$ :

The travel time from station $s_{1} \in S$ to station $s_{2} \in S$ on path $p \in P$

$succ_{{ps_{1} s_{2} }}$ :

is equal to 1 if station $s_{2} \in S$ is successor of station $s_{1} \in S$ on path $p \in P$

ss _l :

The point in time when the stock of parts in bin $l \in L$ is depleted

$L_{ms}^{\max }$ :

The maximum number of part-specific bins of part $m \in M$ at station $s \in S$

$ii_{ms}$ :

The initial inventory of part $m \in M$ at station $s \in S$

td ^max :

The maximum duration of a tour

$N^{ms} \left[ j \right]$ :

The transportation order which is the j-th element of the set $N^{ms}$

$L^{ms} \left[ j \right]$ :

The depletion corresponding to the j-th element of the indexed set $L^{ms}$

$Q^{ms} \left[ j \right]$ :

The number of delivered bins defined by the j-th element of the index set $Q^{ms}$

bigM :

Big number

[A,Z]:

The planning horizon

Variables

$x_{pdt}$ :

Binary variable which is set to 1 if and only if driver $d \in D$ on his/her tour $t \in T$ is assigned to path $p \in P$

$z_{{n_{1} n_{2} dt}}$ :

Binary variable which is set to 1 if and only if transportation order $n_{2} \in N$ is directly processed after transportation order $n_{1} \in N$ on tour $t \in T$ executed by driver $d \in D$

$st_{n}^{N}$ :

Continuous variable which represents the start time of unloading transportation order $n \in N$

$st_{dt}^{T}$ :

Continuous variable which represents the start time of tour $t \in T$ executed by driver $d \in D$

$ft_{dt}^{T}$ :

Continuous variable which represents the finishing time of tour $t \in T$ executed by driver$d \in D$

The MILP model formulation is given as follows:

$$ \min \sum\limits_{p \in P} {\sum\limits_{d \in D} {x_{pd1} } } $$

(1)

$$ \sum\limits_{d \in D} {\sum\limits_{{t \in T^{real} }} {\sum\limits_{{n_{2} \in N}} {z_{{n_{1} n_{2} dt}} } } } = 1\quad\forall n_{1} \in N^{Del} $$

(2)

$$ \sum\limits_{{n_{2} \in N}} {z_{{n{\kern 1pt} n_{2} dt}} } = \sum\limits_{{n_{1} \in N}} {z_{{n_{1} ndt}} }\quad \forall \,n \in N^{Del} ,d \in D,t \in T^{real} $$

(3)

$$ \sum\limits_{p \in P} {x_{pdt} } \le 1\quad\forall d \in D,t \in T^{real} $$

(4)

$$ st_{n}^{N} + pt_{n} \le dd_{n} \quad\forall n \in N^{Del} $$

(5)

$$ \begin{aligned} st_{{n_{1} }}^{N} & + pt_{{n_{1} }} + \sum\limits_{p \in P} {\left( {x_{pdt} \cdot tt_{{ps_{{n_{1} }} s_{{n_{2} }} }} } \right)} - st_{{n_{2} }}^{N} \le \left( {1 - z_{{n_{1} n_{2} dt}} } \right) \cdot bigM \\ & \quad\forall n_{1} ,n_{2} \in N^{Del} ,t \in T^{real} ,d \in D \\ \end{aligned} $$

(6)

$$ \begin{aligned} st_{dt}^{T} & + \sum\limits_{p \in P} {\left( {x_{pdt} \cdot tt_{{ps_{1} s_{{n_{2} }} }} } \right)} \\ & - st_{{n_{2} }}^{N} \le \left( {1 - z_{{1n_{2} dt}} } \right) \cdot bigM\quad\forall n_{2} \in N^{Del} ,t \in T^{real} ,d \in D \\ \end{aligned} $$

(7)

$$ ft_{dt}^{T} + conn^{D} - st_{d(t + 1)}^{T} \le \left( {1 - \sum\limits_{p \in P} {x_{pd(t + 1)} } } \right) \cdot bigM\quad\forall d \in D,t \in T\left| t \right. < t^{\max } $$

(8)

$$ \begin{aligned} st_{n}^{N} & + pt_{n} + \sum\limits_{{n_{1} \in N}} {\left( {x_{pdt} \cdot tt_{pn1} } \right)} - ft_{dt}^{T} \le \left( {1 - z_{n1dt} } \right) \cdot bigM \\ & \quad\forall d \in D,t \in T^{real} ,n \in N^{Del} \\ \end{aligned} $$

(9)

$$ st_{d0}^{T} = A\quad\forall d \in D $$

(10)

$$ ft_{d0}^{T} = A\quad\forall d \in D $$

(11)

$$ ft_{dt}^{T} \le Z\quad\forall d \in D,t \in T^{real} $$

(12)

$$ ft_{dt}^{T} - st_{dt}^{T} \le td^{\max } \quad\forall d \in D,t \in T^{real} $$

(13)

$$ \sum\limits_{p \in P} {x_{pdt} } \ge \sum\limits_{p \in P} {x_{pd(t + 1)} } \quad\forall d \in D,t \in T^{real} \left| {t < t^{\max } } \right. $$

(14)

$$ z_{{n_{1} n_{2} dt}} \le \sum\limits_{p \in P} {x_{pdt} \cdot succ_{{ps_{{n_{1} }} s_{{n_{2} }} }} } \quad\forall n_{1} ,n_{2} \in N^{P} ,d \in D,t \in T^{real} $$

(15)

$$ \sum\limits_{n \in N} {z_{1ndt} } = \sum\limits_{p \in P} {x_{pdt} } \quad\forall d \in D,t \in T^{real} $$

(16)

$$ \sum\limits_{n \in N} {z_{n\left| N \right|dt} } = \sum\limits_{p \in P} {x_{pdt} } \quad\forall d \in D,t \in T^{real} $$

(17)

$$ st_{{N^{ms} \left[ j \right]}}^{N} + pt_{{N^{ms} \left[ j \right]}} \ge ss_{{L^{ms} \left[ j \right]}} \quad\forall s \in S,m \in M^{s} ,i \in 1 \ldots \left| {L^{ms} } \right|,j \in 1 \ldots \left| {N^{ms} } \right|\left| {Q^{ms} \left[ j \right] + ii_{ms} - i \ge L_{ms}^{\max } } \right. $$

(18)

$$ st_{{n_{1} }}^{N} \le st_{{n_{2} }}^{N}\quad \forall s \in S,m \in M^{s} ,n_{1} ,n_{2} \in N^{ms} \left| {dd_{{n_{1} }} < dd_{{n_{2} }} } \right. $$

(19)

$$ \sum\limits_{{n_{1} \in N^{P} }} {\sum\limits_{{n_{2} \in N^{P} }} {z_{{n_{1} n_{2} dt}} \cdot w_{{n_{1} }} - capa^{D} } } \le \left( {1 - \sum\limits_{p \in P} {x_{pdt} } } \right) \cdot bigM\quad\forall d \in D,t \in T^{real} ,p \in P $$

(20)

$$ x_{pdt} \in \left\{ {0,1} \right\}\quad\forall p \in P,d \in D,t \in T^{real} $$

(21)

$$ z_{{n_{1} n_{2} dt}} \in \left\{ {0,1} \right\}\quad\forall n_{1} ,n_{2} \in N,d \in D,t \in T^{real} $$

(22)

$$ st_{n}^{N} \in R^{ + } \quad\forall n \in N^{Del} $$

(23)

$$ st_{dt}^{T} \in R^{ + } \quad\forall d \in D,t \in T $$

(24)

$$ ft_{dt}^{T} \in R^{ + } \quad\forall d \in D,t \in T $$

(25)

A tour is defined by a driver and the number of his/her possible tours. If a driver executes his/her first tour, he/she needs to be considered in the objective function. The objective function (1) minimizes the number of shuttle drivers required to complete all tours. Constraints (2) and (3) are logical constraints which ensure the succession of transportation orders. According to (4) at most one path is assigned to each tour and driver. Constraint (5) ensures that each transportation order is completed on time. The succession of tours is expressed in (6) and (7). Driver schedules are reflected by (8). The finishing time of a tour is determined in (9). In (10) and (11) dummy tours at the beginning of the planning horizon are scheduled for each driver. All tours must be finished within the planning horizon (12). Constraint (13) ensures that maximum tour durations are not exceeded. Constraints (14) enforce a driver-tour assignment to zero, if its previous tour is empty. In (15) the successor relations of two transportation orders are set according to the chosen path of the tour. Dummy transportation orders at the beginning and the end of a tour have exactly one preceding and succeeding transportation order, respectively (16) and (17). Constraint (18) ensures that maximum storage capacities at the stations are not exceeded. Transportation orders are consecutively scheduled according to their due dates (19). Constraints (20) reflect the maximum shuttle capacities. Finally, variable domains are defined in (21–25).