1 Introduction

Within Radio Astronomy, there is a trend to build Radio Telescopes with larger apertures and baselines to increase sensitivity and spatial resolution. In many cases this is realized by sparse arrays of stations and in many cases, each station consists of a sparse array of antennas. The signals of the individual stations or antennas are combined electronically. For Radio Astronomy imaging, part of the processing is done decentralized (beamforming and correlation) and part is done centralized. Prominent recent examples of this type of systems are the Low Frequency Array LOFAR, [18] and the Square Kilometer Array SKA, [7].

Some quantitative predictions of expected power consumption in the centralized processor of the SKA are presented in [10] where the power consumption is estimated to be 7.9 MW for the correlator. This estimate is based on extrapolation of the power consumption of the correlator for the ALMA telescope [42]. Another estimate that reveals the high power consumption characteristics of the SKA telescope is based on a straw-man design for a baseline correlator for the SKA [8]. Within this design, the total power consumption of the correlator boards is estimated to be 5.2 MW.

High power consumption levels are expected for the the centralized processor of the SKA which are hampering the feasibility of modern radio telescopes. Especially the correlator part is contributing significantly to these high levels of power consumption. Based on that, our research question is formulated: “How can the power consumption of the correlator architectures for modern telescopes be significantly reduced?” Because multipliers are the most power consuming elements within a correlator architecture [11], so-called ‘approximate multipliers’ are introduced as an effective measure to reduce power consumption and required silicon area. In this research, we focus on XF correlators (correlation before Fourier Transform) since complexity within these correlators is dominated by the number of multiplications. For FX correlators (Fourier Transform before correlation), the relative contribution of the number of multiplications to the overall complexity is lower [32]. We therefore expect the largest reduction of power consumption and required silicon area by introducing approximate multipliers within XF correlators.

A model of a radio telescope is mathematically described and based on this model, a simulator of a processing pipeline has been constructed, including different types of approximate multipliers. The simulations reveal e.g. the final Signal-to-Noise-Ratio (SNR), Spurious-Free-Dynamic-Range (SFDR) and RMS level (R) within a map. These metrics are used to assess the effects of approximate multipliers and results are presented for different types of multipliers. As an illustration, the constructed correlator model is used to generate maps based on a realistic sky image. At the end of this paper, conclusions are drawn concerning the applicability of approximate multipliers within Radio Telescopes.

2 Related work

In this section, the evolution of digital correlators within Radio Astronomy is presented, followed by an overview of techniques used to optimize correlator architectures in Radio Astronomy. In the third part of this section, as a candidate for further optimization of modern correlator architectures, an overview of approximate computing techniques is given. Finally, approximate recursive multipliers are discussed.

2.1 Evolution of digital correlators

At the end of the previous century, Application Specific Integrated Circuits (ASICs) were designed as core elements within digital correlators. An example of such an ASIC is the NFRA Correlator chip [4]. For this chip, the resolution of the input data was bounded to 2 bits in order to reduce chip area and power consumption. Furthermore, the programmability was limited and only a small set of configurations was available for Radio Astronomy observations. Besides this, the development of these integrated circuits was time consuming and costly. At the same time, due to developments within integrated circuit technology pushed by Moore’s law, huge general purpose processing capacities became gradually available in the form of General Purpose Processors (GPP’s) and Graphics Processing Units (GPU’s). These devices combine high resolution (fixed point and floating point) with programmability. Furthermore, because the Instruction Set Architectures (ISA’s) of these devices last for multiple hardware generations, hardware- and software development are decoupled, enabling re-use of legacy code (in the ideal case). Using these devices, high performance correlator systems have been constructed based on Commercial-of-the-shelf (COTS) components [6, 29]. However, as already predicted in [3], developments in digital circuit technology indicate that power-efficiency gain due to Moore’s law is diminishing rapidly, in spite of reduced transistor sizes. Consequently, when using GPP’s and GPU’s, power consumption will eventually increase proportionally to processing requirements. So, technology progress is not scaling with the size of the Radio Astronomy facilities anymore and power consumption is becoming a bottleneck in realization of these systems in general and correlators more specifically. For that reason, designing dedicated correlator hardware is still a feasible approach. There are basically two approaches for dedicated correlator hardware: using reconfigurable devices like Field Programmable Gate Arrays (FPGA’s) or dedicated correlator ASIC’s. FPGA’s are positioned between programmable processors and ASIC’s. FPGA’s are general purpose devices but, because of the absence of an ISA, programming an FPGA is more involved than programming e.g. a GPP. Furthermore, the range of applications that is covered by a single FPGA configuration is limited because of the small configuration memories and relatively long (re-)configuration times whereas the range of applications between which a GPP or GPU can switch instantaneously is almost infinite due to extremely large program and cache memories. The advantages of FPGA’s are that they can provide large processing capacities due to spatial distribution of tasks and they offer high I/O bandwidths. Furthermore, tailor-made implementations of these tasks make FPGA’s more energy-efficient than GPP’s and GPU’s. Also within Radio Astronomy, FPGA’s are used to build energy-efficient correlator and beamforming systems [16, 22, 23]. Solutions are also sought in combining different technologies. For the realization of a correlator for SKA low, FPGA technology is combined with network switches where the first is being used for signal processing and the latter for data routing [19]. Furthermore, combinations with GPU’s are also made. Yu et al. [44] list several correlators that have been designed in this way among which correlators for the Long Wavelength Array (LWA) and the Murchison Widefield Array (MWA). However, GPU’s and FPGA’s cannot reach energy-efficiency levels that can be achieved by ASIC implementations. Anghel et al. [2] indicated that ASIC solutions can be 1.6 to 4 times more energy-efficient than FPGA solutions. For that reason ASIC implementations of especially the correlator have again been investigated [11, 35, 40]. To further optimize the energy efficiency of correlators, carefully reconsidering the multipliers within the correlator chips is key.

2.2 Optimization of correlator architectures in radio astronomy

In the past, to optimize correlator architectures, knowledge concerning characteristics of the input signal was exploited. Realistic assumptions at that time were that correlator inputs consist of noise signals with a known (Gaussian) amplitude distribution and that the correlation between inputs from different telescopes is low, or formulated differently, the SNR at the input of the correlator is low. Besides that, no interference was assumed. As a consequence, even in cases of coarse quantization, the quantization noise introduced by two- or even single-bit quantizers is uncorrelated between signals from different telescopes. For that reason, one- and two-bit mutlipliers lead to only a small loss in sensitivity. Energy efficiency can even be further increased by using incomplete multipliers where, for specific combinations of input values, not the exact result of a multiplication is produced but an approximation with the aim of reducing hardware complexity. This leads to an additional small loss in sensitivity. The effects of incomplete multipliers on sensitivity has been studied in [9] and [5]. Incomplete multipliers were used within e.g. the NFRA correlator chip [4]. This way it was possible to integrate 1024 correlator lags within a single chip. Because of the trend of constructing correlators based on COTS components, coarse quantization and the use of incomplete multipliers has fallen out of favor in contemporary processing pipelines. However, since Moore’s law is no longer guaranteeing increasing processing capacities per Watt, research on incomplete multipliers has been revived in the area of ‘approximate computing’ [36]. In most cases, the resolution of these ‘new’ incomplete multipliers is larger than 2 bits (and in most cases multiples of 8 bits). Since modern Radio Telescopes like LOFAR and SKA use beamforming to increase the SNR at the inputs of the correlator it is interesting to investigate the use of multibit approximate multipliers in modern processing pipelines for Radio Astronomy imaging.

Fig. 1
figure 1

An 8-bit recursive multiplier requires four 4-bit multipliers (left), each 4-bit multiplier requires four 2-bit multipliers (right). Therefore, sixteen 2-bit multipliers are required to construct an 8-bit multiplier. Adapted from [15]

Full size image

2.3 Approximate computing – the state-of-the-art

Approximate computing is an emerging paradigm that introduces approximations at software-, architecture-, and hardware-level to achieve efficiency benefits [37]. Power-efficiency gains have been demonstrated for error-resilient applications such as radio communication, multimedia digital signal processing, machine learning, and scientific computing [1, 20, 43]. In literature, approximate computing is also coined as best-effort computing, as it executes an algorithm on best-effort bases [26]. It trades the accuracy of algorithms as much as bearable to enhance the computing efficiency as much as possible. Another related term is error-efficient computing, originating from the notion that it prevents as many errors as necessary to execute an algorithm in a resource-efficient manner [38] and [37].

A technique often used in approximate computing is circuit pruning. Wherein, logic gates and/or transistors are reduced in number or complexity to achieve efficiency benefits like chip-area and energy-/power-consumption [33]. It is to be noted that only those parts of a circuit are pruned that have a low probability of usage, and therefore, the approximations do not have a high consequence on the overall quality of output.

Adders and multipliers are the important building blocks of digital signal processing architectures. Unsurprisingly, these building blocks have been widely researched in the approximate computing domain. Gupta et al. [17] presented transistor-level pruning for an approximate full adder circuit, which can be utilized to design multi-bit adders. Another technique for approximate adder circuits is the carry propagation chain simplification or reduction of the critical path to reach the overall sum of two inputs [12, 27, 39]. Additionally, reducing the number of carry-propagation bits reduces power consumption related to the glitches produced during the carry propagation [45].

A multiplication operation includes generating partial products and adding them in a specific shift order to achieve the overall product of two input numbers (operands). The approximation techniques for a multiplier include input truncation, partial product truncation, and pruned addition of partial products [14, 21, 31, 34]. Targeting power-efficiency, gate-level pruning is applied to design a 2-bit multiplier [24]. Such multipliers can be used recursively together with adder trees to form a higher-order (n-bit) multiplier.

2.4 Approximate recursive multipliers

Approximate recursive multipliers prune the recursive multiplication structure to reduce the number of gates and the critical path of the circuit. Such multipliers are (especially) known for their power efficiency benefits [24]. Moreover, such multiplier structures are scalable and provide a huge number of possible approximation choices that help in their optimization process based on the input distribution [25] and [34]. In the context of providing guarantees for approximate multiplication, the worst-case error of approximate recursive multipliers has been demonstrated to be smaller than the worst-case error of some of the other approximate approaches like truncation [28]. Keeping in view the benefits of the approximate recursive multipliers, we have utilized them to study the effect of approximate computation in correlator processing. Here we provide the basic knowledge of approximate recursive multipliers.

Fig. 2
figure 2

Truth tables of 2-bit multipliers. A and C are 2-bit inputs having a range of 0 to 3, shown in decimal numbers. Accurate (M) has all the products correct. M1 has only one output approximated (\(3 \times 3 \mapsto 7\) instead of 9) that produces an error of -2 [24]. M2 has three approximated outputs [34], wherein each approximation produces an error of -1 (e.g., \(1 \times 1 \mapsto 0\) instead of 1). M3 is similar to M1, however, it produces an error of +2 to complement M1 [15]. M4 produces an error of -4 while approximating the product (output) for the same combination of inputs, i.e., A=3 and C=3 [13]

Full size image

To build an n-bit recursive multiplier, four (n/2)-bit sub-multipliers are utilized. Here n is the bit-width of input operands, \(n \in \{4, 8, 16, 32,...\}\). As an example, Fig. 1 illustrates an 8-bit multiplier composed of basic 2-bit multipliers. These 2-bit multipliers generate partial products. The summation of the bit-shifted partial products produces the overall output of an 8-bit recursive multiplier.

Several 2-bit approximate designs have been presented in the literature. The input to output relations (truth tables) of designs used in this paper are shown in Fig. 2. Kulkarni et al. [24] proposed M1 that underestimates one out of the sixteen outputs to improve power-efficiency. It produces an approximate output (7 instead of 9) when both inputs have a value of 3. [34] proposed M2, which reduced the maximum error magnitude to 1 (as compared to 2 in M1). However, M2 increased the error probability to 3/16 (as compared to 1/16 in M1) in case of uniformly distributed inputs. Gillani et al. [15] proposed M3 to introduce a complementary error behavior of M1, i.e., the error produced by M3 is an additive inverse of the error produced by M1. A combination of M1 and M3 within an n-bit multiplier introduces error-cancellation, which improves the quality of the output within accumulation-based algorithms.

Nevertheless, the overestimation in M3 poses a possibility of overflow in n-bit multipliers because it may provide an output higher than that of the exact value. To alleviate the overflow problem while keeping the error cancellation attribute, [13] proposed M4 that underestimates one of the sixteen outputs with a relatively higher error magnitude. Noteworthy, all the approximate 2-bit multipliers (M1, M2, M3, and M4) provide a higher computing efficiency as compared to an accurate 2-bit multiplier.

As shown in Fig. 1, an 8-bit multiplier is composed of sixteen 2-bit multipliers. Any combination of M, M1, M2, M3, and M4 can be utilized to form an 8-bit multiplier. However, the best combinations are chosen based on input distribution and output quality constraints. The following 8-bit designs have been presented in [13]: Acc, Conv2, Conv1, ISH2, and ISH1. The 8-bit Acc multiplier is constructed out of 16 2-bit M multipliers. the Conv designs are based on a combination of M and M1 multipliers whereas the ISH multipliers combine M, M1, M3 and M4 multipliers. The ISH designs are based on the internal-self-healing methodology, which allows higher approximation levels as compared to the conventional methodology (Conv designs) to achieve a higher computing efficiency. For more information, we refer to ([13]). The chip-area and power consumption of the said designs are shown in Table 1. It can be seen that ISH designs provide higher efficiency (lower computing cost) in terms of chip-area and power consumption. The power savings are shown with respect to an accurate 8-bit multiplier (Acc). In Section 4, we will utilize these designs to investigate the feasibility of approximate computing in correlator processing.

3 Model

To assess the effects of approximate multipliers in the correlator of a processing pipeline for Radio Astronomy imaging, a simplified baseband-equivalent mathematical description of an interferometer is constructed. This mathematical description serves as a basis for an executable model in Matlab in which a model of the sky serves as an input and a map is generated as output. Different types of approximate multipliers can be used within the correlator model. Based on the output map, quality metrics are defined that are used to assess the effect of different types of multipliers.

Table 1 Chip-area and power consumption of accurate and approximate 8-bit multiplier designs using 40nm low-power IC technology at 1GHz frequency of operation ([13])
Full size table
Fig. 3
figure 3

Baseband-equivalent model of a 4x4 interferometer with a single Reference Antenna where \(q = -2, -1, 0, 1\)

Full size image
Fig. 4
figure 4

Structure of the Complex Correlator based on approximate multipliers including Automatic Gain Control (AGC) and Analog-to-Digital Converter (ADC)

Full size image

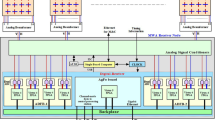
As an example, in Fig. 3, a global overview of the model of a 4x4 interferometer is presented. Antennas are located on a regular square grid. Furthermore, a Reference Antenna is positioned in the middle of the array. A single point source, modeled with a white Gaussian distribution is assumed. Receiver noise is modelled as additive white Gaussian noise at each antenna. The output of the model is a map which is used to determine three evaluation criteria: Signal-to-Noise-Ratio (SNR), Spurious-Free-Dynamic-Range (SFDR) and Root-Mean-Square (RMS) noise level in the map. Below, a formal description of the model and the evaluation criteria are given.

The antennas are placed on a grid with \(\frac{1}{2} \lambda \) spacing. The signals from each antenna are correlated with the signal originating from the Reference Antenna that is placed in the middle of the grid. A complex signal representation is used and each complex correlator is calculating the zero-lag of the crosscorrelation function. The outputs of the complex correlators are fed into a two-dimensional Fast Fourier Transform (2D-FFT) to produce a map. The structure of a complex correlator is presented in Fig. 4.

For both inputs of the correlator, a complex signal representation is used (Re() and Im()). Both the real and imaginary part are represented as floating point numbers and are considered as analog signals that need to be converted into the digital domain before digital multiplication. To optimally exploit the dynamic range of the Analog-to-Digital Converters (ADCs), Automatic-Gain-Control (AGC) is adapting the input signal such that the RMS level is a constant fraction of the maximum input amplitude of the ADC. To avoid clipping to a large extent, within this paper the RMS level is positioned at \(\frac{1}{5}\) th of the maximum amplitude. The RMS levels are used for de-normalization purposes in a later stage. The signal is converted from the analog (read: floating point) domain into the digital domain (read: represented by a limited number of equidistant values). In this paper the output of an ADC consists of 9 bits in a sign-magnitude representation. After analog to digital conversion the complex multiplication is realized by means of 4 approximate real multipliers. Each multiplier calculates the sign of the product based on the sign bits of the inputs and the magnitudes are multiplied by an 8 bit approximate multiplier. The outputs of a multipliers are integrated for a specific number of products and after the summing stage, the resulting values are denormalized with the standard deviations of the two correlated signals, measured by the AGC.

For a general, formal description of the model we define a two dimensional square aperture plane with \(A^2\) antennas where A is assumed to be even. An antenna element is defined by the tuple (p, q) where

$$\begin{aligned} p = -\frac{A}{2}, -\frac{A}{2}+1, ... \frac{A}{2}-1 \end{aligned}$$
(1)
$$\begin{aligned} q = -\frac{A}{2}, -\frac{A}{2}+1, ... \frac{A}{2}-1 \end{aligned}$$
(2)

The set of tuples \((u_p,v_q)\) defines a two-dimensional grid in the uv-plane where each value gives the coordinate of antenna element (p, q) relative to the reference antenna at (0, 0), measured in wavelength \(\lambda \).

$$\begin{aligned} u_p = \frac{p+\frac{1}{2}}{2}\end{aligned}$$
(3)
$$\begin{aligned} v_q = \frac{q+\frac{1}{2}}{2} \end{aligned}$$
(4)

The set of tuples (l, m) defines a two-dimensional grid in the source plane where

$$\begin{aligned} l = -1, -1+\frac{2}{A}, ... 1-\frac{2}{A}\end{aligned}$$
(5)
$$\begin{aligned} m = -1, -1+\frac{2}{A}, ... 1-\frac{2}{A} \end{aligned}$$
(6)

\((l_s,m_s)\) is the position of a single point source in the source plane. A source is assumed to be positioned exactly on the grid within the source plane. The phase difference between the signal received at the reference antenna and the signal received at antenna (p, q) equals \(\theta _{p,q}=2 \pi (u_p l_s + v_q m_s)\). Note that we use the narrowband assumption which implies that a time-delay can be modelled as a phase shift.

The signal at the output of each antenna consist of a noise- and a source component. The noise component is independent for each antenna having a complex Gaussian distribution. The noise components at time t are defined as \(n_{p,q,t} \sim \mathcal {C}\mathcal {N}(0,1)\). The source component, also with a complex Gaussian distribution, is defined as \(s_t \sim \mathcal {C}\mathcal {N}(0,1)\). Finite series of T samples are defined as \(n_{p,q} = [n_{p,q,0}, n_{p,q,1}..., n_{p,q,T-1}]\) and \(s = [s_0, s_1,..., s_{T-1}]\).

Each individual antenna receives a phase shifted version of the source component: \(x_{p,q} = \textrm{e}^{j \theta _{p,q}} \cdot s\). After addition of the noise, the input of the complex correlator can be written as

$$\begin{aligned} y_{p,q}&= \mathrm {SNR_{in}}x_{p,q} + n_{p,q} \end{aligned}$$
(7)

where \(\mathrm {SNR_{in}}\) defines the ratio of the standard deviations of the source- and noise components. \(\mathrm {SNR_{in}}\) is equal for all antennas. After normalization by the AGC and quantization by a mid-treat ADC, the complex valued digital signals are described as

$$\begin{aligned} y_{p,q}^Q&= \textrm{ADC}(\textrm{AGC}(y_{p,q}))\end{aligned}$$
(8)
$$\begin{aligned} s^Q&= \textrm{ADC}(\textrm{AGC}(s)) \end{aligned}$$
(9)

The correlator output or Visibility Function is then described as

$$\begin{aligned} z_{p,q}= y_{p,q}^Q \otimes (s^Q)^{'} \cdot \sigma _{y_{p,q}}~\sigma _s \end{aligned}$$
(10)

where \(\otimes \) indicates the complex innerproduct using approximate multipliers, \('\) the complex conjugate transpose operation, and \(\sigma _{y_{p,q}}\) and \(\sigma _{s}\) are the complex standard deviations of \(y_{p,q}\) and s respectively. Consequently, the number of values integrated within the correlator equals T. The Brightness Distribution (M) is calculated by means of a 2-dimensional Fast Fourier Transform (2DFFT) on the Visiblity Function:

$$\begin{aligned} M = \mid \textrm{2DFFT}(z) \mid \end{aligned}$$
(11)
Fig. 5
figure 5

Maps based on a 16 x 16 antenna array with a point source at position (14 horizontal, 10 vertical) with \(\mathrm {SNR_{in} = 10 dB}\)

Full size image

In Fig. 5a, an example of a map based on a simulation with 16 x 16 antennas is presented. In this case, an input SNR of \(\mathrm {SNR_{in}}\) = 10 dB and ideal multipliers are used. A single source is located at \((l_s,m_s) = (\frac{1}{8}, \frac{5}{8})\). The map is generated by a Matlab implementation of the model defined by expressions (1) to (11). Because the source is positioned exactly on the grid within the source plane, all energy is confined into a single point in the final Brightness Distribition M. In case of a non-ideal (non-linear) correlator, source energy will be spread over other points within the Brightness Distribution as well. To assess the quality of the map produced by the model described above, three metrics are defined: \(\mathrm {SNR_{dB}}\), \(\mathrm {SFDR_{dB}}\) and \(\mathrm {R_{dB}}\). Their definition is explained below. To determine the metrics, four different values that are distilled from M are defined: the power at the calculated position of the point source \(S_M\), the sum of the power values of all the other points \(N_M\) which ideally consists of only noise contributions but might also contain spurious components due to instrumental effects, the largest component in the map besides the source signal \(P_M\) and the RMS level over all other points in the map (\(R_M\)).

$$\begin{aligned} S_M&= M_{l_s,m_s}\end{aligned}$$
(12)
$$\begin{aligned} N_M&= \sqrt{\left( \sum _{l,m} (M_{l,m})^2 \right) } - S_M\end{aligned}$$
(13)
$$\begin{aligned} P_M&= \max _{l,m \mathrm {,~where~} (l,m) \ne (l_s, m_s)} M_{l,m} \end{aligned}$$
(14)

To calculate the RMS level of the noise contributions in the map, the following is defined

$$\begin{aligned} \mu&= \frac{\left( \sum _{l,m}^{} M_{l,m} \right) - M_{l_s,m_s}}{A^2-1} \end{aligned}$$
(15)
$$\begin{aligned} R_{M}&= \sqrt{\frac{1}{A^2-1}\sum _{l,m \text {,~where~} (l,m) \ne (l_s, m_s)}{} (M_{l,m}-\mu )^{2}} \end{aligned}$$
(16)

The final Signal-to-Noise-Ratio \(\mathrm {SNR_{dB}}\), Spurious Free Dynamic Range \(\mathrm {SFDR_{dB}}\) and RMS level \(\mathrm {R_{dB}}\) on dB scale are then defined as

$$\begin{aligned} \mathrm {SNR_{dB}}&= 10~ ^{10} \! \log \left( \frac{S_M}{N_M} \right) \end{aligned}$$
(17)
$$\begin{aligned} \mathrm {SFDR_{dB}}&= 10~ ^{10} \! \log \left( \frac{P_M}{N_M} \right) \end{aligned}$$
(18)
$$\begin{aligned} \mathrm {R_{dB}}&= 20~ ^{10} \! \log \left( R_M \right) \end{aligned}$$
(19)

4 Results

In Fig. 5b the same system setup as for Fig. 5a is used where the ideal multipliers are replaced by ISH1 multipliers. Within these maps, the point source is clearly visible. For all other points in the map, power levels are much lower (more than 35 dB).

To assess the quality of the maps for different approximate multipliers, Monte Carlo simulations have been done using the same setup as for Fig. 5 and the performance metrics, defined in the previous section have been determined. To explore the dependency of the performance metrics \(\mathrm {SNR_{dB}}\), \(\mathrm {SFDR_{dB}}\) and \(\mathrm {R_{dB}}\) on the SNR at the input of each antenna, simulations for a large SNR input range (from -20 to +40 dB) are conducted. All simulation results are averaged over 25 simulation runs. To have manageable simulation times, the number of samples to be integrated within a single run T is relatively small. Simulation results are based on \(T = 64\) for the following multiplier architectures: ideal, accurate (Acc), Conventional 1 (Conv1), Conventional 2 (Conv2), Internal Self Healing 1 (ISH1) and Internal Self Healing 2 (ISH2) multipliers. For the ideal and ISH1 multiplier architectures, simulations are done for \(T = 256\) and \(T=1024\) as well. The results for \(\mathrm {SNR_{dB}}\) are presented in Fig. 6.

Fig. 6
figure 6

SNR within the map as a function of the SNR at the input of each individual antenna

Full size image
Fig. 7
figure 7

Distribution of the RMS value within the map as a function of the SNR at the input of each individual antenna. Note that a limited \(\mathrm {SNR_{in}}\) range is used

Full size image

Figure 6 shows that up to an input SNR of approximately 10 dB, all architectures give similar performance where an increased \(\mathrm {SNR_{in}}\) leads to an increased \(\mathrm {SNR_{dB}}\). Beyond 10 dB the curves for the non-ideal multiplier architectures deviate from the ideal curve. The largest deviation is seen for the ISH1 curve. This deviation is caused by quantization and clipping by the ADC, and approximation within the multiplier.

In Fig. 7, the distribution of the 25 simulations is presented for the ideal- and ISH1 cases, a limited \(\mathrm {SNR_{in}}\) range (5-25 dB) and \(T=1024\). For an \(\mathrm {SNR_{in}}<\) 10 dB, the two distributions are overlapping. For \(\mathrm {SNR_{in}} \ge \) 10 dB the SNR values for ISH1 case spread over a larger \(\mathrm {SNR_{dB}}\) range, due to the approximation within the ISH1 multipliers.

To analyse the effects that can be observed in Figs. 6 and 7, first the effects introduced by the ADC are analysed. According to [41] the quantization noise is uncorrelated with the input signal if the RMS level of the noise added to the input signal is larger than the quantization step size. In case the RMS level of the noise is smaller than the quantization step size, the quantization noise between the different antennas becomes correlated and higher \(\mathrm {SNR_{in}}\) does not lead to higher \(\mathrm {SNR_{dB}}\). In case of the accurate multiplier and \(5 \sigma \)-clipping, the quantization noise is uncorrelated up to approximately 30 dB. In Fig. 6, the curve for the accurate multiplier indeed starts to deviate from the ideal curve in case \(\mathrm {SNR_{in}}>\) 30 dB. All other multiplier schemes show similar behavior except for ISH1 where the curve starts to deviate beyond 10 dB which is due to the coarser approximation within this multiplier. Because of this, using the ISH1 scheme is considered to be the worst case scenario and is therefore used to further investigate the effect of longer integration lengths, using 256 and 1024 samples. Quadrupling the integration length should lead to an improvement of \(\mathrm {SNR_{dB}}\) by 6 dB which can indeed be seen from Fig. 6 for \(\mathrm {SNR_{in}}<\) 10 dB. Beyond this limit, increasing the integration length does not increase \(\mathrm {SNR_{dB}}\) because of the correlation of noise introduced by quantization and the approximation. Another important observation is that, for \(\mathrm {SNR_{in}}<\) 10 dB, \(\mathrm {SNR_{dB}}\) is not significantly affected by the approximation in ISH1.

Simulation results for the Spurious Free Dynamic Range (\(\mathrm {SFDR_{dB}}\)) and the RMS noise level (\(\mathrm {R_{dB}}\)) are presented in Figs. 8 and 9 respectively.

Fig. 8
figure 8

SFDR within the map as a function of the SNR at the input of each individual antenna

Full size image
Fig. 9
figure 9

RMS of the noise within the map as a function of the SNR at the input of each individual antenna

Full size image

For the Spurious Free Dynamic Range (\(\mathrm {SFDR_{dB}}\)), similar effects as for \(\mathrm {SNR_{dB}}\) can be observed. However, the effects of approximation are more emphatically present. For the accurate, Conv1 and Conv2 multipliers the \(\mathrm {SFDR_{dB}}\) starts to deviate from ideal values beyond 30 dB. The coarser approximation by the ISH2 multiplier leads to deviations beyond 20 dB and ISH1 leads to deviations beyond 10 dB. But, also for \(\mathrm {SFDR_{dB}}\), the performance is not significantly affected for \(\mathrm {SNR_{in}}<\) 10 dB when increasing integration lengths.

Figure 9 presents the RMS level of the noise within the map as a function of \(\mathrm {SNR_{in}}\) for the same cases as described above. For the ideal multiplier, the \(\mathrm {SNR_{in}}\) domain can be roughly divided into two parts. Up to -10 dB, increasing \(\mathrm {SNR_{in}}\) hardly improves \(\mathrm {R_{dB}}\) because noise is dominating the input signals at the antennas. Beyond -10 dB, increasing \(\mathrm {SNR_{in}}\) leads to reduced RMS levels in the map. In case of using the accurate or one of the approximate multipliers, increasing \(\mathrm {SNR_{in}}\) eventually leads to correlated quantization noise which results in diminishing returns with respect to \(\mathrm {R_{dB}}\). This effect is strongest in case of the ISH1 approximate multiplier. Beyond 10 dB, increasing \(\mathrm {SNR_{in}}\) does not lead to lower \(\mathrm {R_{dB}}\). Furthermore, up to \(\mathrm {SNR_{in}}\) = 10 dB, the RMS level in the map is reduced with 3 dB when quadrupling the integration length for all multiplier architectures.

Based on Figs. 6, 8 and 9, we conclude that, for \(\mathrm {SNR_{in}}<\) 10 dB, the performance of all approximate multipliers is similar to the performance of the accurate multiplier for relatively small integration lengths. To explore the effects of approximate multipliers in case of longer integration lengths, simulations are done for the ISH1 multiplier and \(\mathrm {SNR_{in}} =\) 0 dB. ISH1 was chosen because in this design, the effects of approximation are most prominent.

The results of these simulations are displayed in Table 2.

Table 2 Performance of ISH1 for \(\mathrm {SNR_{in}}\) = 0 dB
Full size table

From Table 2 it is seen that also for longer integration lengths, \(\mathrm {SNR_{dB}}\) and \(\mathrm {SFDR_{dB}}\) increase with approximately 3 dB when quadrupling the integration length and \(\mathrm {R_{dB}}\) reduces with approximately 3 dB when quadrupling the integration length.

Fig. 10
figure 10

Part of the map “the dancing ghosts” from [30] that is used to generate the received antenna signals

Full size image
Fig. 11
figure 11

Map that is created using a correlator with ideal 8-bit multipliers. SNR = 0 dB, T = 256 samples. The scale is normalized based on the maximum value within this map

Full size image
Fig. 12
figure 12

Map that is created using a correlator with ISH1 multipliers. SNR = 0 dB, T = 256 samples. The scale is normalized based on the maximum value within the map of Fig. 11

Full size image
Fig. 13
figure 13

Difference between the maps based on ideal 8-bit multipliers and ISH1 multipliers. Note that the scale differs from the scale in Figs. 11 and 12

Full size image

To evaluate the effects of approximate multipliers using more realistic data, the model described above has been extended to a square array of 128 by 128 antennas (A = 128). Consequently, the source plane consists of a 128 x 128 grid as well. As a model, a 128 x 128 pixel part of the sky from “the dancing ghosts” image from [30] has been used where a pixel of the sky map is used as a single point source where the power of a point source is determined by the intensity in the map (linear scale). Based on the 128 x 128 point sources, the resulting signal at each individual antenna element has been determined. The SNR at each antenna element was set at 10 dB and maps have been generated in case of a correlator based on ideal 8-bit multipliers and in case of a correlator based on ISH1 multipliers. Results have been obtained by integration over 16K samples. In Fig. 10 the original noise-free part of the sky is presented. The map has been normalized with the maximum value in the map and noise has been added (10 dB SNR). Figure 11 gives the resulting map in case of a correlator with ideal 8-bit multipliers, and Fig. 12 gives the resulting map in case of a correlator with ISH1 multipliers. Both maps are normalized with the maximum value in the map based on ideal multipliers (Fig. 11). Figure 13 presents the difference between the maps in Figs. 11 and 12.

Visual inspection of Figs. 11 and 12 shows that artefacts introduced by quantization (Fig. 11) and approximate multiplication (Fig. 12) are below the sky noise. Furthermore, the difference between the two maps is smaller than \(1.5 10^{-2}\) and as expected, the variance in areas with higher intensity is larger.Also, no artefacts are observed.

5 Conclusion

In order to find the answer to the research question “How can the power consumption of the correlator architectures for modern telescopes be significantly reduced?”, the use of approximate multipliers within the correlator of signal processing pipelines for modern Radio Telescopes has been investigated. Approximate multipliers produce results with reduced precision compared to accurate multipliers. The benefit is that these multipliers are smaller (occupy less area on an integrated circuit) and consume less energy per multiplication. The next question that is addressed in this paper is then “How does the reduced precision affect the quality of the maps that are produced using a correlator with approximate multipliers?”. To quantify the effects on the quality of the map, 3 performance metrics have been defined: Signal-to-Noise-Ratio (\(\mathrm {SNR_{dB}}\)), Spurious-Free-Dynamic-Range (\(\mathrm {SFDR_{dB}}\)) and Root-Mean-Square noise level (\(\mathrm {R_{dB}}\)) in the map. A simulation model has been constructed based on an array of 16 by 16 antennas and a single point source. Besides the reference case (no quantization, ideal multipliers), the use of 5 different types of multipliers has been simulated. Besides an accurate 8-bit multiplier, 4 approximate multipliers are analysed. Based on the simulations, the following conclusions can be drawn:

  • Up to 10 dB \(\textrm{SNR}\) at the input of the individual antennas, there is no (noticeable) effect introduced by the approximate multipliers that have been used in this paper. This is illustrated for the ISH1 approximate multiplier which was identified as the worst case.

  • Approximation leads to noise correlation. Different approximate multipliers exhibit different levels of noise correlation. The maximum \(\mathrm {SNR_{in}}\) at which approximation does not lead to noise correlation differs for different approximate multipliers. Out of the set of approximate multipliers that have been investigated the best performing ones (Conv1 and Conv2) introduce no (noticable) effects up to \(\mathrm {SNR_{in}}\) = 30 dB.

  • Significant power reduction can be achieved by exploiting approximate multipliers. When using the approximate multiplier ISH1 which can be used up to 10 dB input SNR, 19% energy can be saved compared to using accurate multipliers. When using Conv1 which can be used up to 30 dB input SNR, 12% energy can be saved.

The analysis in this paper uses 8-bit multipliers as a starting point. The results indicate that, as long as the SNR at the input of the correlator is low, more aggressive approximation could be applied, leading to even higher energy savings. To further improve energy efficiency of correlators, it is interesting to investigate flexible multiplier architectures where the type of multiplier can be matched with the SNR at the input. In case of low SNR, a multiplier exploiting aggressive approximation can significantly reduce power consumption. In high SNR scenarios, more accurate multipliers are required leading to relatively high levels of power consumption. Being able to chose the optimal multiplier when configuring the correlator will lead to significant lower energy consumption when considering multiple, different observations. Related to this, it is interesting to investigate how to exploit the concepts of approximate computing when using Field Programmable Gate Array (FPGA) boards to realize correlators. In this paper, ASIC implementations of multipliers are used. However, these implementations do not map optimally onto the basic blocks of FPGA’s. For that reason a bottom-up approach should be used where FPGA basic blocks are used to construct approximate multipliers which can lead to significant energy savings when using FPGA’s. Furthermore, the aim is to further exploit the approximate computing paradigm within other parts of the signal processing chain besides the correlator, to increase energy efficiency.