Skip to main content
SpringerLink
Log in

Auctions with endogenous participation and an uncertain number of bidders: experimental evidence

  • Original Paper
  • Published:
Experimental Economics Aims and scope Submit manuscript

Abstract

Attracting bidders to an auction is a key factor in determining revenue. We experimentally investigate entry and bidding behavior in first-price and English clock auctions to determine the revenue implications of entry. Potential bidders observe their value and then decide whether or not to incur a cost to enter. We also vary whether or not bidders are informed regarding the number of entrants prior to placing their bids. Revenue equivalence is predicted in all four environments. We find that, regardless of whether or not bidders are informed, first-price auctions generate more revenue than English clock auctions. Within a given auction format, the effect of informing bidders differs. In first-price auctions, revenue is higher when bidders are informed, while the opposite is true in English clock auctions. The optimal choice for an auction designer who wishes to maximize revenue is a first-price auction with uninformed bidders.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4

Similar content being viewed by others

Notes

  1. The revenue equivalence theorem addresses the choice of mechanism for independent private value auctions with an exogenous number of bidders. It states that bidders are indifferent between standard auction formats, and thus that any such format will generate the same expected revenue. See e.g., Vickrey (1961), Myerson (1981) and Heydenreich et al. (2009).

  2. See e.g., Cox et al. (1982) and Coppinger et al. (1980).

  3. Auctions with few participating bidders are empirically relevant. For instance, in all outer continental shelf auctions for oil and gas run between 1954 and 1979, the modal number of participating bidders was one. These auctions attracted a single bidder \(36.89\%\) of the time, and two bidders \(19.24\%\) of the time.

  4. See e.g., Hendricks et al. (1987, 1989, 1993, 1994) and Hendricks and Porter (1988).

  5. The finding that entry exceeds risk neutral predictions is also observed in other auction settings. See e.g., Palfrey and Pevnitskaya (2008) and Smith and Levin (2002).

  6. We thank an anonymous reviewer for this point. A model with heterogeneous risk attitudes may be able to explain our data. Characterizing equilibrium in such an environment is particularly challenging, because potential bidders would self-select into auctions based on their value and their degree of risk aversion. Since we are primarily interested in the revenue ranking of the auction formats and information structures, we leave this for future research. For an analysis of heterogeneous risk preferences in first-price auctions in which potential bidders do not observe their value prior to entry, so that self-selection into auctions is determined by a single variable, see Pevnitskaya (2004). Palfrey and Pevnitskaya (2008) finds behavior in the lab consistent with heterogeneous risk-averse potential bidders.

  7. For a theoretical analysis of bidding in auctions with an uncertain number of bidders see e.g., Matthews (1987), McAfee and McMillan (1987b), Harstad et al. (1990) and Levin and Ozdenoren (2004). Isaac et al. (2012) experimentally examines both second and first-price auctions with an uncertain number of bidders, and argues that their data can be explained by a model with heterogeneous risk preferences.

  8. Without private information, equilibrium entry is either asymmetric and deterministic (McAfee and McMillan 1987a; Engelbrecht-Wiggans 1993) or symmetric and stochastic (Engelbrecht-Wiggans 1987; Levin and Smith 1994; Smith and Levin 1996; Ye 2004; Li and Zheng 2009). Some variations allow for private information on dimensions other than value to be observed prior to entry. For example, potential bidders observe their participation costs in Cox et al. (2001) and Moreno and Wooders (2011), and observe their degree of (heterogeneous) risk aversion in Pevnitskaya (2004).

  9. Examples include Smith and Levin (2002), Palfrey and Pevnitskaya (2008), Reiley (2005) and Roberts and Sweeting (2013).

  10. Other theoretical papers which analyze similar environments include Samuelson (1985), Stegeman (1996), Lu (2009) and Cao and Tian (2010). When private values are observed prior to entry, most theoretical analysis has focused on second-price auctions e.g., Campbell (1998), Tan and Yilankaya (2006), Miralles (2008) and Cao and Tian (2008).

  11. The case in which both bidders’ valuations and participation costs are both private information has also been studied theoretically for second-price auctions by Green and Laffont (1984) and Cao and Tian (2009).

  12. There is also a literature in which multiple sellers of homogeneous goods compete for bidders via auction format. See Peters and Severinov (1997) and Preston McAfee (1993) for theoretical analysis of such an environment, and Ivanova-Stenzel and Salmon (2004, 2008a, b, 2011) for experimental analysis. Peters and Severinov (2006) analyses second-price auctions where sellers compete via reserve prices, and Anwar et al. (2006) uses e-Bay auctions data to test this model.

  13. Equilibrium in a model in which symmetric potential bidders are risk averse would involve more aggressive bidding in first-price auctions, and a higher entry threshold. See Menezes and Monteiro (2000) for proof of this assertion. As will be discussed in the results section, this is not consistent with our data. A model in which potential bidders have heterogeneous risk preferences may be able to explain our data.

  14. See e.g., Myerson (1981) and Heydenreich et al. (2009).

  15. Table 1 in the online supplement contains a breakdown of the number of times in a session each possible realizations of c is used.

  16. Subjects who do not enter can repeatedly play tic-tac-toe can play against the computer until the auction for that period ends. They know that results of each game do not affect their payoffs. Palfrey and Pevnitskaya (2008) investigates the effect on entry into first-price auctions of having non-entrants play a version of rock–paper–scissors against the computer. In their setup, bidders learn their value after entry, and are informed. They find that the use of rock–paper–scissors reduces, but does not eliminate, over-entry.

  17. In English clock auctions the winning bid is not observed.

  18. In eleven sessions, this was done at the beginning of the session, and in the other eight it was done at the end.

  19. In addition to the nineteen sessions we report, three sessions were run in which the data is unusable. In two sessions, due to a problem with a parameter in the software, subjects received instructions for the incorrect treatment (Informed instead of Uninformed). In the other, a subject had participated in a previous session. The results we report are robust to including the data from this session, but we feel that it it better to exclude it so that our session-level data is independent. We also discard the data from the first four sessions we ran in which bidders in the auction were informed of the number of bidders, but this information was not (in our view) sufficiently salient. This is because when the only bidder in a FPI auction submits a positive bid, the interpretation is unclear. The environment in which subjects participate is a complex one, and it may not seem natural or intuitive to subjects that one can win an auction with a bid of zero. Our impression was that subjects who made positive bids in FPI auctions did so due to limited attention, memory, or salience. This was a cause for concern for two reasons: First, one treatment variable was revealing information about the number of bidders. If this information was not salient enough, our implementation of the treatment was weak. Second, this would affect the comparability of our results as it would artificially exacerbate the treatment differences in revenue between FPI and ECI auctions. Recall that in the ascending clock auction with only one bidder, the clock automatically stopped at a price of zero. After the first four sessions, we decided to omit these sessions to be conservative and not stack the deck against the ECI treatment. We then modified the software so that when there was only one bidder in an FPI (or ECI) auction, this bidder was reminded that she could obtain the good with a bid of zero. Although some single bidders in FPI still bid positive amounts, the frequency is lower and reduces in the second half. Following Roth (1994, p. 287), we feel it is important to openly disclose the process through which the data was collected.

  20. A copy of the instructions (translated from the original Spanish) for sessions with uninformed bidders, as well as instructions for the risk elicitation task, can be found in the online supplement.

  21. As reference, lunch can be purchased on UFM’s campus for Q25, and student workers in the library earn Q24 an hour.

  22. The results for payoffs mirror those of revenue. In the interest of brevity, we therefore relegate a discussion of these results to the online supplement.

  23. The fact that first-price auctions generate more revenue than English clock auctions with a fixed number of bidders is well known. See e.g., Cox et al. (1982). Our result thus shows that this revenue ranking is robust to allowing potential bidders to choose to enter the auction after observing their value.

  24. The test statistic is undefined because the lowest observation in FPU auctions is bigger than the largest observation in FPI auctions.

  25. Splitting the data into the cases where \(m=1\) and does not affect the results of non-parametric tests on revenue ranking except in the FPU and FPI case and the trivial case of English clock auctions with \(m=1\) (where the auction ends immediately at a price of zero).

  26. Using two sample Kolmogorov–Smirnov tests, we cannot find differences in the distribution for any pairwise treatment comparison: FPI versus FPU (\(D=0.0389\), n.s.); ECI versus ECU (\(D=0.0160\), n.s.); ECU versus FPU (\(D=0.0115\), n.s.); ECI versus FPI (\(D=0.0463\), n.s.).

  27. n.s. indicates that the test is insignificant at conventional levels.

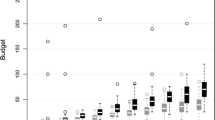
  28. Since potential bidders know both c and their value when they make entry decisions, both of these variables are of interest. Figure 2 illustrates average entry by c. Figure 1 in the online supplement illustrates average entry by value. Probit regressions reported in Table 6 examine the effect of both c and value on entry, all else constant.

  29. The relevant test statistics are FPI: sign test, \(w=9\), \(p=0.002\), FPU: sign test, \(w=10\), \(p=0.001\), ECI: sign test, \(w=9\), \(p=0.002\) and ECU: sign test, \(w=10\), \(p=0.001\). There is some heterogeneity in entry behavior. While the majority of participants over-enter on average, several enter less than predicted. Figure 2 in the online supplement illustrates this.

  30. Note however that our experimental design has low power to evaluate entry, because we cannot observe the entry thresholds of potential bidders. Aycinena et al. (2017) uses a Becker–DeGroot–Marschack mechanism to directly elicit threshold entry strategies and find no differences in entry thresholds between FPI and ECI.

  31. Our results on equality of entry across treatments differ considerably from those of Ivanova-Stenzel and Salmon (2011), who found that potential bidders with higher values were more likely to enter English clock auctions, while those with low values were more likely to enter first-price auctions. However, our results are not directly comparable. In their setting potential bidders had to choose to enter one format or the other, since they study an environment in which multiple sellers of a homogeneous good compete for bidders via auction format, rather than price. Their result suggests that in such an environment, a seller may be able to attract bidders away from competitors by utilizing an English clock auction. However, in the environments we study, the seller need not compete against other sellers for bidders. As such, a potential bidder with a high value was likely to enter, regardless of the format, and a potential bidder with a low value was likely not to enter, regardless of format.

  32. Observing a large number of participants in the previous period may affect participation, regardless of the auction format. Note that \(m_{it-1}\) does not take into account changes in auction format which occurs three times over the course of the experiment. However, results are robust in terms of direction, statistical significance and magnitude of the coefficients, if we estimate models that drops the preceding period if a different auction format was used.

  33. Table 2 in the online supplement contains results without the lagged number of bidders.

  34. Notice that the magnitude of the marginal effect corresponding to \(c_{it}\) is approximately between 3.0 to 3.7 times as large as the marginal effect corresponding to \(v_{it}\). If this is driven by expected payoffs, then one would expect that the return to an incremental increase in \(c_{it}\) is approximately three times that of an incremental increase in \(v_{it}\). We find that the average increase in payoffs resulting from an incremental increase in \(v_{it}\) is 0.290. This is calculated by taking the average payoff at each possible value, and then taking the average change in payoff resulting from a one unit increase in value.

  35. An interesting avenue of research would be to examine, in the spirit of List and Lucking-Reiley (2002), the entry behavior of experienced market participants relative to neophytes to determine if experienced potential bidders entry less frequently.

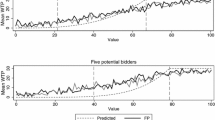
  36. Bidding behavior has been studied extensively in the literature. In English clock auctions, bidders tend to bid their values in accordance with theory [see e.g., Coppinger et al. (1980)]. In first-price auctions, however, bidders tend to overbid relative to risk-neutral Nash predictions [see e.g., Kagel and Levin (1993)].

  37. Table 3 in the online supplement breaks down the summary statistics on bidding by the number of bidders in the auction.

  38. For English clock auctions, we are restricted to cases where \(m\ge 2\).

  39. It is unlikely that collusion drives underbidding in English clock auctions, given that subjects are randomly re-matched after each period, and were not able to communicate. Further, in any given session, subjects participate in both English clock and first-price auctions. If bidders manage to coordinate on a collusive bidding strategy in English clock auctions, they would do the same in first-price auctions.

  40. Regressions which test whether or not bids in English clock auctions correspond to theory are in Table 4 of the online supplement. The estimates are consistent with the results of the non-parametric tests.

  41. Regressions which test whether or not bids in first-price auctions correspond to theory are in Table 5 in the online supplement. The estimates are consistent with the results of the non-parametric tests.

  42. The test statistic is undefined because the lowest average bid deviation in FPU auctions is bigger than the largest average bid deviation in FPI auctions.

  43. Bid deviations in first-price auctions are not explained by optimal response to over-entry by bidders. If this were the case, entrants would reduce their bids relative to the equilibrium bid predictions (which assume equilibrium entry behavior), which is the opposite of what we observe.

  44. Palfrey and Pevnitskaya (2008) consider heterogeneous risk preferences in an environment where bidders learn their value after entry, and finds that heterogeneous risk attitudes are consistent with observed behavior.

  45. The number of observations for English clock auctions is less than those for first-price auctions since we do not observe the bids of winning bidders in the former.

  46. Note that this does not affect the valuation of the predicted winning bidder, but does effect their equilibrium bids. It is, of course, possible that an increase in the opportunity cost of entry is large enough that the predicted winning bidder chooses not to enter the auction.

References

  • Anwar, S., McMillan, R., & Zheng, M. (2006). Bidding behavior in competing auctions: Evidence from eBay. European Economic Review, 50(2), 307–322.

    Article  Google Scholar 

  • Aycinena, D., Bejarano, H., & Rentschler, L. (2017). Informed entry in auctions. International Journal of Game Theory. https://doi.org/10.1007/s00182-017-0583-9.

    Article  Google Scholar 

  • Camerer, C., & Lovallo, D. (1999). Overconfidence and excess entry: An experimental approach. American Economic Review, 89(1), 306–318.

    Article  Google Scholar 

  • Campbell, C. (1998). Coordination in auctions with entry. Journal of Economic Theory, 82(2), 425–450.

    Article  Google Scholar 

  • Cao, X., & Tian, G. (2008). Second-price auctions with differentiated participation costs. Working paper.

  • Cao, X., & Tian, G. (2009). Second-price auctions with two-dimensional private information on values and participation costs. Working paper.

  • Cao, X., & Tian, G. (2010). Equilibria in first-price auctions with participation costs. Games and Economic Behavior, 69(2), 258–273.

    Article  Google Scholar 

  • Chen, Y., Katuscak, P., & Ozdenoren, E. (2013). Why can’t a woman bid more like a man? Games and Economic Behavior, 77(1), 181–213.

    Article  Google Scholar 

  • Coppinger, V., Smith, V., & Titus, J. (1980). Incentives and behavior in English, Dutch and sealed-bid auctions. Economic Inquiry, 18(1), 1–22.

    Article  Google Scholar 

  • Cox, J., Roberson, B., & Smith, V. (1982). Theory and behavior of single object auctions. Research in Experimental Economics, 2, 1–43.

    Google Scholar 

  • Cox, J., Dinkin, S., & Swarthout, J. (2001). Endogenous entry and exit in common value auctions. Experimental Economics, 4(2), 163–181.

    Article  Google Scholar 

  • Dyer, D., Kagel, J., & Levin, D. (1989). Resolving uncertainty about the number of bidders in independent private-value auctions: An experimental analysis. Rand Journal of Economics, 20(2), 268–279.

    Article  Google Scholar 

  • Engelbrecht-Wiggans, R. (1987). On optimal reservation prices in auctions. Management Science, 33(6), 763–770.

    Article  Google Scholar 

  • Engelbrecht-Wiggans, R. (1993). Optimal auctions revisited. Games and Economic Behavior, 5(2), 227–39.

    Article  Google Scholar 

  • Engelbrecht-Wiggans, R., & Katok, E. (2005). Experiments on auction valuation and endogenous entry. Advances in Applied Microeconomics: A Research Annual, 13, 169–193.

    Article  Google Scholar 

  • Fischbacher, U. (2007). z-Tree: Zurich toolbox for ready-made economic experiments. Experimental Economics, 10(2), 171–178.

    Article  Google Scholar 

  • Fischbacher, U., & Thoni, C. (2008). Excess entry in an experimental winner-take-all market. Journal of Economic Behavior & Organization, 67(1), 150–163.

    Article  Google Scholar 

  • Goeree, J., & Holt, C. (2005). An explanation of anomalous behavior in models of political participation. American Political Science Review, 99(02), 201–213.

    Article  Google Scholar 

  • Green, J., & Laffont, J. (1984). Participation constraints in the vickrey auction. Economics Letters, 16(1), 31–36.

    Article  Google Scholar 

  • Greiner, B. (2004). An online recruitment system for economic experiments. Working Paper.

  • Harstad, R., Kagel, J., & Levin, D. (1990). Equilibrium bid functions for auctions with an uncertain number of bidders. Economics Letters, 33(1), 35–40.

    Article  Google Scholar 

  • Hendricks, K., & Porter, R. H. (1988). An empirical study of an auction with asymmetric information. American Economic Review, 78(5), 865–883.

    Google Scholar 

  • Hendricks, K., Porter, R. H., & Boudreau, B. (1987). Information, returns, and bidding behavior in ocs auctions: 1954–1969. Journal of Industrial Economics, 35(4), 517–542.

    Article  Google Scholar 

  • Hendricks, K., Porter, R. H., & Spady, R. H. (1989). Random reservation prices and bidding behavior in OCS drainage auctions. Journal of Law and Economics, 32(2), S83–S106.

    Article  Google Scholar 

  • Hendricks, K., Porter, R. H., & Tan, G. (1993). Optimal selling strategies for oil and gas leases with an informed buyer. American Economic Review, 83(2), 234–239.

    Google Scholar 

  • Hendricks, K., Porter, R. H., & Wilson, C. A. (1994). Auctions for oil and gas leases with an informed bidder and a random reservation price. Econometrica, 62(6), 1415–1444.

    Article  Google Scholar 

  • Heydenreich, B., Müller, R., Uetz, M., & Vohra, R. (2009). Characterization of revenue equivalence. Econometrica, 77(1), 307–316.

    Article  Google Scholar 

  • Holt, C., & Laury, S. (2002). Risk aversion and incentive effects. American Economic Review, 92(5), 1644–1655.

    Article  Google Scholar 

  • Isaac, M., Pevnitskaya, S., & Schnier, K. (2012). Individual behavior and bidding heterogeneity in sealed bid auctions where the number of bidders is unknown. Economic Inquiry, 50(2), 516–533.

    Article  Google Scholar 

  • Ivanova-Stenzel, R., & Salmon, T. (2004). Bidder preferences among auction institutions. Economic Inquiry, 42(2), 223–236.

    Article  Google Scholar 

  • Ivanova-Stenzel, R., & Salmon, T. (2008a). Revenue equivalence revisited. Games and Economic Behavior, 64(1), 171–192.

    Article  Google Scholar 

  • Ivanova-Stenzel, R., & Salmon, T. (2008b). Robustness of bidder preferences among auction institutions. Economic Inquiry, 46(3), 355–368.

    Article  Google Scholar 

  • Ivanova-Stenzel, R., & Salmon, T. (2011). The high/low divide: Self-selection by values in auction choice. Games and Economic Behavior, 73(1), 200–214.

    Article  Google Scholar 

  • Kagel, J., & Levin, D. (1993). Independent private value auctions: Bidder behaviour in first-, second-and third-price auctions with varying numbers of bidders. Economic Journal, 103(419), 868–879.

    Article  Google Scholar 

  • Klemperer, P. (2002). What really matters in auction design. Journal of Economic Perspectives, 16(1), 169–189.

    Article  Google Scholar 

  • Levin, D., & Ozdenoren, E. (2004). Auctions with uncertain numbers of bidders. Journal of Economic Theory, 118(2), 229–251.

    Article  Google Scholar 

  • Levin, D., & Smith, J. (1994). Equilibrium in auctions with entry. American Economic Review, 84(3), 585–599.

    Google Scholar 

  • Li, T., & Zheng, X. (2009). Entry and competition effects in first-price auctions: Theory and evidence from procurement auctions. Review of Economic Studies, 76(4), 1397–1429.

    Article  Google Scholar 

  • List, J., & Lucking-Reiley, D. (2002). Bidding behavior and decision costs in field experiments. Economic Inquiry, 40(4), 611–619.

    Article  Google Scholar 

  • Lu, J. (2009). Auction design with opportunity cost. Economic Theory, 38(1), 73–103.

    Article  Google Scholar 

  • Matthews, S. (1987). Comparing auctions for risk averse buyers: A buyer’s point of view. Econometrica, 55(3), 633–46.

    Article  Google Scholar 

  • McAfee, R., & McMillan, J. (1987a). Auctions with entry. Economics Letters, 23(4), 343–347.

    Article  Google Scholar 

  • McAfee, R., & McMillan, J. (1987b). Auctions with a stochastic number of bidders. Journal of Economic Theory, 43(1), 1–19.

    Article  Google Scholar 

  • McAfee, P. R. (1993). Mechanism design by competing sellers. Econometrica, 61(6), 1281–1312.

    Article  Google Scholar 

  • Menezes, F., & Monteiro, P. (2000). Auctions with endogenous participation. Review of Economic Design, 5(1), 71–89.

    Article  Google Scholar 

  • Miralles, A. (2008). Intuitive and noncompetitive equilibria in weakly efficient auctions with entry costs. Mathematical Social Sciences, 56(3), 448–455.

    Article  Google Scholar 

  • Moreno, D., & Wooders, J. (2011). Auctions with heterogeneous entry costs. RAND Journal of Economics, 42(2), 313–336.

    Article  Google Scholar 

  • Myerson, R. B. (1981). Optimal auction design. Mathematics of Operations Research, 6(1), 58–73.

    Article  Google Scholar 

  • Palfrey, T., & Pevnitskaya, S. (2008). Endogenous entry and self-selection in private value auctions: An experimental study. Journal of Economic Behavior & Organization, 66(3), 731–747.

    Article  Google Scholar 

  • Peters, M., & Severinov, S. (1997). Competition among sellers who offer auctions instead of prices. Journal of Economic Theory, 75(1), 141–179.

    Article  Google Scholar 

  • Peters, M., & Severinov, S. (2006). Internet auctions with many traders. Journal of Economic Theory, 130(1), 220–245.

    Article  Google Scholar 

  • Pevnitskaya, S. (2004). Endogenous entry in first-price private value auctions: The self-selection effect. Working paper.

  • Reiley, D. H. (2005). Experimental evidence on the endogenous entry of bidders in internet auctions. In A. Rapoport & R. Zwick (Eds.), Experimental business research (Vol. II, pp. 103–121). Springer.

  • Roberts, J., & Sweeting, A. (2013). When should sellers use auctions? American Economic Review, 103(5), 1830–1861.

    Article  Google Scholar 

  • Roth, A. (1994). Lets keep the con out of experimental econ.: A methodological note. Empirical Economics, 19(2), 279–89.

    Article  Google Scholar 

  • Samuelson, W. (1985). Competitive bidding with entry costs. Economics Letters, 17(1–2), 53–57.

    Article  Google Scholar 

  • Smith, J., & Levin, D. (1996). Ranking auctions with risk averse bidders. Journal of Economic Theory, 68(2), 549–561.

    Article  Google Scholar 

  • Smith, J., & Levin, D. (2002). Entry coordination in auctions and social welfare: An experimental investigation. International Journal of Game Theory, 30(3), 321–350.

    Article  Google Scholar 

  • Stegeman, M. (1996). Participation costs and efficient auctions. Journal of Economic Theory, 71(1), 228–259.

    Article  Google Scholar 

  • Tan, G., & Yilankaya, O. (2006). Equilibria in second-price auctions with participation costs. Journal of Economic Theory, 130(1), 205–219.

    Article  Google Scholar 

  • Vickrey, W. (1961). Counterspeculation, auctions, and competitive sealed tenders. Journal of Finance, 16(1), 8–37.

    Article  Google Scholar 

  • Ye, L. (2004). Optimal auctions with endogenous entry. The BE Journal of Theoretical Economics, 4(1), 8.

    Google Scholar 

Download references

Acknowledgements

Financial support from the International Foundation for Research in Experimental Economics is gratefully acknowledged. Thanks also to Jorge Chang Urrea, Pedro Monzón Alvarado and Diego Fernandez for outstanding research assistance. We have benefited from comments and suggestions from participants in seminars at Universidad Francisco Marroquín, Florida State University, the Economic Science Institute at Chapman University, the International ESA Conference in Chicago, the CeDEx Workshop at the University of Nottingham and the Antigua Experimental Economics Conference.

Author information

Authors and Affiliations

  1. Facultad de Economía, Universidad del Rodario, Calle 12C No. 6-25, Bogotá, D.C., Colombia

    Diego Aycinena

  2. Department of Economics and Finance, Utah State University, 3500 Old Main Hill, Logan, UT, 84322, USA

    Lucas Rentschler

Authors
  1. Diego Aycinena
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Lucas Rentschler
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Lucas Rentschler.

Electronic supplementary material

Below is the link to the electronic supplementary material.

Supplementary material 1 (PDF 180 kb)

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Aycinena, D., Rentschler, L. Auctions with endogenous participation and an uncertain number of bidders: experimental evidence. Exp Econ 21, 924–949 (2018). https://doi.org/10.1007/s10683-017-9558-8

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10683-017-9558-8

Keywords

JEL Classifications

Search

Navigation