Abstract
We theoretically and experimentally investigate a game in which exactly one person should make a costly effort to achieve a socially efficient outcome. This setting is commonly known as the volunteer’s dilemma. We implement one-way communication by allowing one player to send a message indicating whether she intends to volunteer and investigate the message’s effects on behavior and efficiency in the subsequent game. We theoretically demonstrate that there are asymmetric mixed-strategy equilibria in the volunteer’s dilemma and argue that one of these is likely to emerge through one-way communication. The experimental data support this notion. We find that the actions of both the sender and receiver of the message are crucially affected by the cheap talk stage and that efficiency in the volunteer’s dilemma increases with one-way communication.
Similar content being viewed by others
Notes
In Industrial Organization, the process of simultaneously developing an industry standard, the best of which will be adopted by all companies, can be modeled in a similar way. The development of freeware software is also an example of a volunteer’s dilemma.
For an overview of coordination failures in experiments, see Devetag and Ortmann (2007).
One-way communication is defined as allowing one randomly selected player to send a message containing information on the strategy she plans to play.
The equilibrium is ‘risky’ in the sense that the opponent’s deviations from the unique equilibrium strategy can cause substantial losses.
See Diekmann (1985).
In the following, we denote \( \hat{q}(k) \) simply as \( \hat{q} \) to economize on notation.
M stands for “mixing”, D for “defecting”.
We implicitly assume that the k players have the accurate belief that n – k players will play \( s^{NV} \) with certainty. Below, we will show that players can commit themselves to playing \( s^{NV} \) by means of cheap talk, inducing this belief.
Intuitively, the overall probability that at least one player volunteers is higher if k out of the k players mix (as is the case from the perspective of the n − k players in D who choose to not volunteer with certainty) than if k − 1 out of the k players mix (as is the case from the perspective of one of the k players in M choosing mixed strategies).
When k = 1, n − 1 decision-makers play \( s^{NV} \) for certain, and thus the remaining player does not mix between strategies but plays \( s^{V} \) with a probability of 1. This also follows from Statement 1 with \( { \lim }\,k \downarrow 1.\)
The proof is relegated to Appendix 1.
Note that behavior in Cooper et al. (1992) becomes more efficient despite that messages in their coordination games are not self-signaling, indicating that the second criterion might be of lesser importance empirically.
While Aumann (1990) and Farrell and Rabin (1996) provide only verbal definitions of the credibility conditions, Baliga and Morris (2002) offer a formalization. They omit the case of indifference in their formal discussion, but, in the analysis of an exemplary game, implicitly make the same assumption as is made here. Furthermore, this assumption is supported by experimental findings on individuals’ reluctance to send non-truthful messages in sender-receiver games despite an incentive to lie (e.g., Gneezy 2005).
We also conducted robust-rank order tests and generally obtained similar results. In cases in which significance levels differ (we considered three levels: p < 0.10, p < 0.05, p < 0.01), we also present the results of this test (p RRO ).
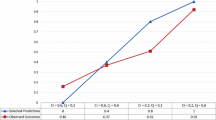
Figures depicting time series of the main variables (signal sent, volunteer rate and payoffs) can be found in Figs. 1, 2 and 3 in Online Appendix 2 of the Electronic Supplementary Material. While it takes a few periods for senders to converge towards the asymmetric mixed-strategy equilibrium announcement, the other variables seem rather stable over the course of time. The higher amplitude of variables after the message “not volunteer” can be explained by the fact that these series are partly based on very few observations.
In our sample, subjects did not choose the strategy they announced in advance in only 4.5 % of the cases.
Considering the second half of the experiment only (after the 10th round), the share does not differ from the prediction of the asymmetric mixed strategy equilibrium (0.45 vs. 0.50; p WSR = 0.31).
Note that this difference is only significant after taking all observations from the communication treatment into account. When dividing up the communication treatment by observed signals, the profits do not differ from the baseline treatment on conventional significance levels, compared to cases in which the signal is \( m^{NV} \) (p MWU = 0.17) or to those in which the signal is \( m^{V} \) (p MWU = 0.13).
A message in this setting consists of two pieces of information: First, the sender announces that she will not volunteer; second, she appoints a second player as “volunteer”. While the first part can be self-signaling and self-committing, the second part merely establishes a focal point. It is thus conceivable that the non-senders believe the component of the message that refers to the sender but ignore the appointment. In this case, we would expect to observe the same asymmetric mixed strategy equilibrium as in our setting. However, because for the non-senders the payoff of the asymmetric mixed strategy equilibrium equals the payoff of volunteering, we conjecture that players will acknowledge the appointment.
References
Aumann, R. J. (1990). Nash equilibria are not self-enforcing. In J. J. Gabszewicz, J.-F. Richard, & L. A. Wolsey (Eds.), Economic decision-making: Games, econometrics and optimization. Amsterdam: Elsevier.
Baliga, S., & Morris, S. (2002). Co-ordination, spillovers, and cheap talk. Journal of Economic Theory, 105(2), 450–468.
Blume, A., & Ortmann, A. (2007). The effects of costless pre-play communication: Experimental evidence from games with pareto-ranked equilibria. Journal of Economic Theory, 132(1), 274–290.
Burton, A., & Sefton, M. (2004). Risk, pre-play communication and equilibrium. Games and Economic Behavior, 46(1), 23–40.
Cooper, R., DeJong, D. V., Forsythe, R., & Ross, T. W. (1989). Communication in the battle of the sexes game: Some experimental results. RAND Journal of Economics, 20(4), 568–587.
Cooper, R., DeJong, D. V., Forsythe, R., & Ross, T. W. (1992). Communication in coordination games. Quarterly Journal of Economics, 107(2), 739–771.
Crawford, V. (1998). A survey of experiments on communication via cheap talk. Journal of Economic Theory, 78(2), 286–298.
Darley, J. M., & Latané, B. (1968). Bystander intervention in emergencies: Diffusion of responsibility. Journal of Personality and Social Psychology, 8(41), 377–383.
Devetag, G., & Ortmann, A. (2007). When and why? A critical survey on coordination failure in the laboratory. Experimental Economics, 10(3), 331–344.
Diekmann, A. (1985). Volunteer’s dilemma. Journal of Conflict Resolution, 29(4), 605–610.
Diekmann, A. (1993). Cooperation in an asymmetric volunteer’s dilemma game: theory and experimental evidence. International Journal of Game Theory, 22, 75–85.
Farrell, J. (1987). Cheap talk, coordination, and entry. RAND Journal of Economics, 18(1), 34–39.
Farrell, J., & Rabin, M. (1996). Cheap talk. Journal of Economic Perspectives, 10(3), 103–118.
Fischbacher, U. (2007). Z-tree: Zurich toolbox for ready-made economic experiments. Experimental Economics, 10(2), 171–178.
Gneezy, U. (2005). Deception: The role of consequences. American Economic Review, 95(1), 384–394.
Greiner, B. (2004). An online recruitment system for economic experiments. In K. Kremer & V. Macho (Eds.), Forschung und wissenschaftliches rechnen 2003 (pp. 79–93). Goettingen: Gesellschaft fuer Wissenschaftliche Datenverarbeitung.
Myatt, D. P., & Wallace, C. (2008). An evolutionary analysis of the volunteer’s dilemma. Games and Economic Behavior, 62(1), 67–76.
Stauf, J. (2012). Essays on behavior under risk and uncertainty. Dissertation, University of Cologne.
Van Huyck, J., Battalio, R., & Beil, R. (1990). Tacit coordination games, strategic uncertainty, and coordination failure. American Economic Review, 80(1), 234–248.
Van Huyck, J., Battalio, R., & Beil, R. (1991). Strategic uncertainty, equilibrium selection, and coordination failure in average opinion games. Quarterly Journal of Economics, 106(3), 885–911.
Weesie, J. (1993). Asymmetry and timing in the volunteer’s dilemma. Journal of Conflict Resolution, 37(3), 569–590.
Weesie, J. (1994). Incomplete information and timing in the volunteer’s dilemma: A comparison of four models. Journal of Conflict Resolution, 38, 557–585.
Acknowledgments
We thank Vitali Gretschko, Bernd Irlenbusch, Sebastian Lotz, Axel Ockenfels, Bettina Rockenbach, Peter Werner, the participants of the ESA International Conference 2013 and two anonymous referees for helpful comments. A former version of the paper using a different setting is part of the second author’s dissertation (Stauf 2012). Financial support from the German Research Foundation (DFG) through the Leibniz program and the research unit “Design and Behavior” (FOR 1371) is gratefully acknowledged.
Author information
Authors and Affiliations
Corresponding author
Electronic supplementary material
Below is the link to the electronic supplementary material.
Appendix 1: Proof of Statement 2
Appendix 1: Proof of Statement 2
We have characterized three types of Nash equilibria in the volunteer’s dilemma:
-
(1)
All players play pure strategies: one player chooses \( s^{V} \), and all remaining players choose \( s^{NV} \).
-
(2)
Some players play the pure strategy \( s^{NV} \); the remaining k players play symmetric mixed strategies.
-
(3)
All players play symmetric mixed strategies.
Obviously, if at least one player chooses \( s^{V} \), the single best reply is to choose \( s^{NV} \), and hence an equilibrium in which some players play the pure strategy \( s^{V} \) and the remaining players mix cannot exist.
First, we will show that there are no further types of equilibria in this game. Second, we will show that we have identified all equilibria of the types characterized above.
There could exist two further types of equilibria:
-
(4)
Some players play the pure strategy \( s^{NV} \), while the remaining players mix with asymmetric probabilities.
-
(5)
All players play mixed strategies, but they mix with asymmetric probabilities.
In the following, we will prove that equilibria as described in (4) and (5) do not exist by showing that, in equilibrium, if \( k \) players mix across strategies while the remaining \( n - k \) players choose \( s^{NV} \) with certainty, the mixing probability must be the same for all \( k \) players in subgroup \( M \).
Assume that player \( m \in M \) chooses \( s^{NV} \) with probability \( q_{m} , 0 < q_{m} < 1. \) In a mixed strategy equilibrium, player \( m \) must be indifferent between \( s^{V} \) and \( s^{NV} \), and hence the expected payoff \( \varPi \left( {s^{NV} } \right) \) of playing \( s^{NV} \) must be equal to the sure payoff \( \varPi \left( {s^{V} } \right) \) of playing \( s^{V} \).
From \( \varPi \left( {s^{V} } \right) = V - C \) and \( \varPi \left( {s^{NV} } \right) = \mathop \prod \limits_{{i \in M{ \setminus }m}} q_{i} L + \left( {1 - \mathop \prod \limits_{{i \in M{ \setminus }m}} q_{i} } \right)V \), it follows that
This also holds for any other player \( l \in M \) with \( l \ne m \); hence, \( \mathop \prod \limits_{{i \in M{ \setminus }m}} q_{i} = \mathop \prod \limits_{{i \in M{ \setminus }l}} q_{i} \Rightarrow \frac{{\mathop \prod \nolimits_{i} q_{i} }}{{q_{m} }} = \frac{{\mathop \prod \nolimits_{i} q_{i} }}{{q_{l} }} \).
It follows that \( q_{m} = q_{l } \quad \forall m,l \in M \).
The same argument holds if \( k = n \), i.e., if all players choose mixed strategies.
Moreover, there could exist further equilibria of the types described in (2) and (3), i.e., players could mix with symmetric probabilities that are different from \( \hat{q} (k) \) and \( q^{*} \), respectively.
Consider the equilibrium described in (2). As we have shown, for a given player \( m \in M \) to be indifferent between \( s^{V} \) and \( s^{NV} \), the product of the probabilities with which the remaining mixing players \( M{ \setminus }m \) choose \( s^{NV} \) must equal a constant \( \frac{C}{V - L} \). Obviously, if any other player \( j \in M \) chose a probability lower (higher) than \( \hat{q}\left( k \right) \), this condition could only be met if a third player \( r \in M \) chose a probability higher (lower) than \( \hat{q}\left( k \right) \). It follows that there are no equilibria in which \( k \) players mix with symmetric probabilities that are different from \( \hat{q}\left( k \right) \).
Again, the same argument holds if \( k = n \); if all players choose mixed strategies, there are no equilibria in which players mix with symmetric probabilities that are different from \( q^{*} . \) □
Rights and permissions
About this article
Cite this article
Feldhaus, C., Stauf, J. More than words: the effects of cheap talk in a volunteer’s dilemma. Exp Econ 19, 342–359 (2016). https://doi.org/10.1007/s10683-015-9442-3
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10683-015-9442-3