Abstract
We use a limited information environment to assess the role of confusion in the repeated voluntary contributions game. A comparison with play in a standard version of the game suggests, that the common claim that decision errors due to confused subjects biases estimates of cooperation upwards, is not necessarily correct. Furthermore, we find that simple learning cannot generate the kind of contribution dynamics commonly attributed to the existence of conditional cooperators. We conclude that cooperative behavior and its decay observed in public goods games is not a pure artefact of confusion and learning.




Similar content being viewed by others
Notes
The choices of subjects who are confused may also be more likely to be influenced by objectively irrelevant contextual cues in language and other merely procedural details of the experiment. Ferraro and Vossler (2010), for example, report that “many subjects believe they are playing a sort of stock market game” (p. 24) and they conjecture that this might be caused by the “investment language” used in many voluntary contributions experiments. Fosgaard, Hansen and Wengström (2011) find that more subjects are able to identify the dominant strategy when the game is presented in a “take” as compared to a “give frame.”
In contrast to repetition, which represents a sequence of decision rounds within the same group of subjects, the term ‘experience’ means that subjects play the game again with a different group.
The term ‘warm glow’ was introduced by Andreoni (1993). Based on a similar thought, some authors have proposed games with an interior equilibrium prediction to test economic theory. This literature typically reports a lower level of excess cooperation. See, e.g., Ziegelmeyer and Willinger (2001) and the references they cite.
Gintis et al. (2003) explain similar dynamics with an evolutionary approach.
Besides potential interaction effects between heterogeneous social preferences and decision errors, there are other arguments why subjects may learn differently between strategic and individual choice situations. See, for example, Duersch et al. (2010), who explore how subjects learn to play a Cournot-Duopoly game against computers that are programmed to follow one of various learning algorithms.
For studies on the comparative power of alternative learning models see, among others, Gale et al. (1995), Erev and Roth (1998), Chen and Tang (1998), Feltovich (2000), Janssen and Ahn (2006). Camerer and Ho (1999) propose a weighted model with choice reinforcement and belief-based (fictitious play) learning as two special cases. Using data from a large class of experimental games, they show that learning is best explained by a combination of both.
These authors use a large sample from the general population in Denmark. They also run a follow-up experiment with standard student subjects in which even fewer subjects correctly answer this question.
Ferraro and Vossler (2010) suggest that subjects may use the actions of others as an indication of profit-maximizing behavior. Note that such “herding” is ruled out by our design.
We are grateful to an anonymous referee who suggested this treatment as a robustness check.
Contributions in the Standard Condition are very similar to contributions in the experiments where the standard VCM was played in a second phase of the Learning Condition (the averages are 7.24 in the Standard Condition and 8.25 and 7.73 after the minimum and limited information condition, respectively). A Mann-Whitney U-test (two tailed, applied on group averages) is insignificant at p>0.28 (p>0.80) if we compare the contributions in the Standard Condition with the results in the standard VCM played in a second phase after the Minimum (Limited) Information Condition. We therefore pool the data of all experiments that involve the standard VCM. Note that this result is consistent with our finding, that a reduction of confusion (which may happen in this case because of learning with limited information), does not necessarily lead to lower contributions in the Standard Condition.
This findings is in line with Ferraro and Vossler (2010), who also observe that contributions decrease faster in the standard VCM game as compared to their learning condition involving virtual players.
A Kolmogorov-Smirnov test to test the null hypothesis of identical distributions is insignificant (p>0.19).
The typical argument claims that, since a rational selfish player chooses the lowest possible contribution (i.e. zero), any confusion would lead to a positive and therefore higher contribution.
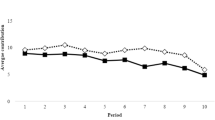
Comparing the over-all average group contributions across the conditions reveals that there are no significant differences (p>0.35, Mann-Whitney U-test). The average group contribution per period is 39.1 percent in the Standard Condition and 40.0 percent in the Learning Condition.
Initially, we planed to refine the distribution allowing for more mass on the past choice. Analyzing the data, we found that the median of choices for both experimental conditions is approximately in the middle of the support, which is consistent with assuming choices with equal probabilities. So we decided to stick with this simple formulation.
We also simulated the learning model with different initial choices. Even when starting with extreme values (only 0 or 20) simulated behavior quickly converges to that generated by starting values drawn from the empirical distributions.
The average mean square error of the simulation is almost five times larger in the Standard Condition (3.21 vs. 0.66 points).
Fischbacher, Gächter and Fehr (2001) report 50 percent conditional cooperators.
For the full regression results see Appendix A.2.
An important difference of our approach to agent-based modeling is that we study the behavior of human subjects rather than the outcomes generated by computerized agents.
This assumption differs slightly from a traditional reinforcement-learning model in that it allows for “strategy similarity” (Sarin and Vahid 2004). In our formulation admissible strategies are not only seen as similar but even identical by the subjects.
References
Andreoni, J. (1988). Why free ride? Strategies and learning in public goods experiments. Journal of Public Economics, 37(3), 291–304.
Andreoni, J. (1995). Cooperation in public-goods experiments: kindness or confusion? The American Economic Review, 85(4), 891–904.
Andreoni, J. (1993). An experimental test of the public goods crowding-out hypothesis. The American Economic Review, 83(5), 1317–1327.
Anderson, S. P., Goeree, J. K., & Hol, C. A. (1998). A theoretical analysis of altruism and decision error in public goods games. Journal of Public Economics, 70, 297–323.
Blundell, R., & Bond, S. (1998). Initial conditions and moment restrictions in dynamic panel-data models. Journal of Econometrics, 87, 115–143.
Brandts, J., & Schram, A. (2001). Cooperation and noise in public goods experiments: applying the contribution function approach. Journal of Public Economics, 79, 399–427.
Bush, R. R., & Mosteller, F. (1955). Stochastic models for learning. New York: Wiley.
Camerer, C. F. (2003). Behavioral game theory: experiments in strategic interaction. Princeton: Priceton University Press.
Camerer, C. F., & Ho, T.-H. (1999). Experience-weighted attraction learning in normal form games. Econometrica, 67, 827–874.
Chen, Y., & Khoroshilov, Y. (2003). Learning under limited information. Games and Economic Behavior, 44, 1–25.
Chen, Y., & Tang, F. (1998). Learning and Incentive Compatible Mechanisms for Public Goods Provision: An Experimental Study. Journal of Political Economy, 106, 633–662.
Cookson, R. (2000). Framing effects in public goods experiments. Experimental Economics, 3, 55–79.
Croson, R. (1996). Partners and strangers revisited. Economics Letters, 53, 25–32.
Duersch, P., Kolb, A., Oechssler, J., & Schipper, B. C. (2010). Rage against the machines: how subjects play against learning algorithms. Economic Theory, 43(3), 407–430.
Erev, I., & Roth, A. E. (1998). Predicting how people play games: reinforcement learning in experimental games with unique, mixed strategy equilibria. American Economic Review, 88, 848–881.
Feltovich, N. (2000). Reinforcement-based vs. belief-based learning models in experimental asymmetric-information games. Econometrica, 68, 605–641.
Ferraro, P. J., & Vossler, C. A. (2010). The source and significance of confusion in public goods experiments. The B.E. Journal in Economic Analysis & Policy, 10(1), 53.
Fischbacher, U. (2007). Z-Tree: Zurich toolbox for readymade economic experiments. Experimental Economics, 10(2), 171–178.
Fischbacher, U., & Gächter, S. (2010). Social preferences, beliefs, and the dynamics of free riding in public good experiments. The American Economic Review, 100(1), 541–556.
Fosgaard, T., Hansen, L. G., & Wengström, E. (2011). “Framing and misperceptions in a public good experiment” FOI working paper 2011/11, University of Copenhagen, Institute of Food and Resource Economics.
Fudenberg, D., & Levine, D. (1998). Learning in games. European Economic Review, 42, 631–639.
Gale, J., Binmore, K., & Samuelson, L. (1995). Learning to be imperfect: the ultimatum game. Games and Economic Behavior, 8(1), 56–90.
Gintis, H., Bowles, S., Boyd, R., & Fehr, E. (2003). Explaining altruistic behavior in humans. Evolution and Human Behavior, 24(3), 153–172.
Gode, D. K., & Sunder, S. (1993). Allocative efficiency of markets with zero-intelligence traders: market as a partial substitute for individual rationality. Journal of Political Economy, 101, 119–137.
Goeree, J. K., Holt, C. A., & Laury, S. K. (2002). Private costs and public benefits: Unraveling the effects of altruism and noisy behavior. Journal of Public Economics 83, 255–276.
Goetze, D., & Orbell, J. M. (1988). Understanding and cooperation in social dilemmas. Public Choice, 57, 275–279.
Greiner, B. (2003). An online recruitment system for economic experiments. In K. Kremer & V. Macho (Eds.), Forschung und wissenschaftliches Rechnen.
Herrnstein, R. J. (1970). On the law of effect. Journal of the Experimental Analysis of Behavior, 13(2), 243–266.
Holt, C. A., & Laury, S. K. (2008). Theoretical explanations of treatment effects in voluntary contributions experiments. In C. R. Plott & V. S. Smith (Eds.), Handbook of experimental economic results (Vol. 1, pp. 846–855). Elsevier: New York. Part 6.
Houser, D., & Kurzban, R. O. (2002). Revisiting kindness and confusion in public goods experiments. The American Economic Review, 92(4), 1062–1069.
Huck, S., Normann, H.-T., & Öchssler, J. (1999). Learning in Cournot oligopoly—an experiment. Economic Journal, 109, 80–96.
Isaac, R. M., Walker, J., & Thomas, S. (1984). Divergent evidence on free riding: an experimental examination of possible explanations. Public Choice, 43(1), 113–149.
Isaac, R. M., & Walker, J. (1988). Group size effects in public goods provision: the voluntary contributions mechanism. Quarterly Journal of Economics, 103, 179–199.
Janssen, M. A., & Ahn, T.-K. (2006). Learning, signaling, and social preferences in public-good games. Ecology and Society, 11(2), 21.
Keser, C., & van Winden, F. (2000). Conditional cooperation and voluntary contributions to public goods. Scandinavian Journal of Economics, 102, 23–39.
Kocher, M. G., Martinsson, P., & Visser, M. (2008). Does stake size matter for cooperation and punishment? Economic Letters, 99, 508–511.
Kreps, D. M., Milgrom, P., Roberts, J., & Wilson, R. B. (1982). Rational cooperation in the finitely repeated prisoners’ dilemma. Journal of Economic Theory, 27(2), 245–252.
Kurzban, R. O., & Houser, D. (2005). An experimental investigation of cooperative types in human groups: a complement to evolutionary theory and simulations. Proceedings of the National Academy of Sciences of the United States of America, 102(5), 1803–1807.
Ledyard, J. O. (1995). Public goods: a survey of experimental research. In J. H. Kagel & A. E. Roth (Eds.), The handbook of experimental economics (pp. 111–194). Princeton: Princeton University Press.
Marwell, G., & Ames, R. E. (1980). Experiments on the provision of public goods II: provision points, stakes, experience, and the free-rider problem. American Journal of Sociology, 85(4), 926–937.
Mookherjee, D., & Sopher, B. (1994). Learning behavior in an experimental matching pennies game. Games and Economic Behavior, 7, 62–91.
Muller, L., Sefton, M., Steinberg, R., & Vesterlund, L. (2008). Strategic behavior and learning in repeated voluntary contribution experiments. Journal of Economic Behavior & Organization, 67(3–4), 782–793.
Palfrey, T. R., & Prisbrey, J. E. (1996). Altruism, reputation and noise in linear public goods experiments. Journal of Public Economics, 61, 409–427.
Palfrey, T. R., & Prisbrey, J. E. (1997). Anomalous behavior in public goods experiments: how much and why? The American Economic Review, 87, 829–846.
Sarin, R., & Vahid, F. (2004). Strategy similarity and coordination. Economic Journal, 114, 506–527.
Selten, R., & Stöcker, R. (1986). End behavior in sequences of finite prisoner’s dilemma games: a learning theory approach. Journal of Economic Behavior & Organization, 7, 47–70.
Van Huyck, J. B., Battalio, R. C., & Rankin, F. W. (2007). Selection dynamics and adaptive behavior without much information. Economic Theory, 33(1), 53–65.
Ziegelmeyer, A., & Willinger, M. (2001). Strength of the social dilemma in a public goods experiment: an exploration of the error hypothesis. Experimental Economics, 4(2), 131–144.
Acknowledgements
We are grateful for financial support by the Austrian Science Fund (FWF) under Projects No. P17029 and S10307-G14 as well as by the Faculty of Profession Research Grant Scheme of the University of Adelaide. We thank the editor Jordi Brandts, Simon Gächter, Martin Sefton and three anonymous referees for helpful comments and suggestions.
Author information
Authors and Affiliations
Corresponding author
Electronic Supplementary Material
Below is the link to the electronic supplementary material.
Appendix
Appendix
1.1 A.1 Details of the learning model
So we arrive at an extremely simple learning model. Define the set of players as I={1,2,3,4} and the action space as C={0,1,…,20}. Denote the contribution of person i ∈I in period t∈{1,2,…,20} as \(c_{t}^{i}\in C\). The player uses the payoffs p and the own choices of the last two periods to determine the contribution in the current period (if possible). The attraction of choosing a certain contribution \(A(c_{t}^{i})\) is therefore a function of the two past contributions and the payoffs in the two last periods:
After having observed the two last outcomes given the choices made, for the next round individuals only consider choices which are closer to the choice that resulted in a higher payoff.Footnote 23 Suppose \(c_{t-1}^{i}\) was greater than \(c_{t-2}^{i}\) and the payoff in period t−1 was greater than in period t−2, then the individual only chooses values in the interval from the midpoint between the two previous choices to the maximum choice (20). For equal profits in periods t−1 and t−2 the support is [0,20], as then the history contains no information about in which direction to go. Moreover, the support will also be the whole spectrum of possible choices if the previous two choices were identical.
To find the region of choices (the support) that satisfies these conditions given the history, define the changes in choices and payoffs between periods t−1 and t−2 as


Then we can introduce a variable \(d_{t}^{i}\) that tells us whether the player wants to choose a number closer to the higher (\(d_{t}^{i}=1\)) or the lower of the previous choices (\(d_{t}^{i}=-1\)):
Note that if either the profits or the previous choices have not changed between periods t−2 and t−1 then we have \(d_{t}^{i}=0\). Denoting the admissible support for period t as \(C_{t}^{i}\) we have:
Next, we have to specify which point within the admissible range will be chosen. The simplest assumption is that subjects are equally likely to choose any element of \(C_{t}^{i}\).Footnote 24 To implement this we set the attraction for a choice in \(C_{t}^{i}\) equal to one, while the attraction of a contribution outside of \(C_{t}^{i}\) is set to zero:
To arrive at the desired uniform distribution over the support \(C_{t}^{i}\) we transform attractions into probabilities using the following rule:
1.2 A.2 Dynamic-panel estimation
We estimated a dynamic panel, which allows for contributions to depend on past own contributions and on past contributions of other group members. By design any unobserved panel-level effects are correlated with the lagged own contributions. For this reason we used the Arellano-Bond-Bover GMM estimator with additional moment conditions developed in Blundell and Bond (1998) that can handle this endogeneity problem. Table 3 reports the results.
Rights and permissions
About this article
Cite this article
Bayer, RC., Renner, E. & Sausgruber, R. Confusion and learning in the voluntary contributions game. Exp Econ 16, 478–496 (2013). https://doi.org/10.1007/s10683-012-9348-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10683-012-9348-2
Keywords
- Voluntary contribution mechanism
- Public goods experiments
- Learning
- Limited information
- Confusion
- Conditional cooperation