Smoothing, Decomposing and Forecasting Mortality Rates

Abstract

The Lee–Carter (LC) model represents a landmark paper in mortality forecasting. While having been widely accepted and adopted, the model has some limitations that hinder its performance. Some variants of the model have been proposed to deal with these drawbacks individually, none coped with them all at the same time. In this paper, we propose a Three-Component smooth Lee–Carter (3C-sLC) model which overcomes many of the issues simultaneously. It decomposes mortality development into childhood, early-adult and senescent mortality, which are described, individually, by a smooth variant of the LC model. Smoothness is enforced to avoid irregular patterns in projected life tables, and complexity in the forecasting methodology is unaltered with respect to the original LC model. Component-specific schedules are considered in projections, providing additional insights into mortality forecasts. We illustrate the proposed approach to mortality data for ten low-mortality populations. The 3C-sLC captures mortality developments better than a smooth improved version of the LC model, and it displays wider prediction intervals. The proposed approach provides actuaries, demographers, epidemiologists and social scientists in general with a unique and valuable tool to simultaneously smooth, decompose and forecast mortality.

Appendices

Appendix A Comparison in Terms of Methods and Populations

This appendix will be devoted to a broader comparison among different mortality forecasting models and populations. We will asses performance of the proposed Three-Component smooth Lee–Carter (3C-sLC) model against several competitors by means of goodness-of-fit assessments and out-of-sample forecast exercises.

Specifically, we compare the proposed 3C-sLC model with other four alternative forecasting methods:

• the smooth Lee–Carter variant by Delwarde et al. (2007): sLC

• the functional data approach of the LC by Hyndman and Ullah (2007): HU

• the CP-splines introduced by Camarda (2019): CP-S

• the three-component segmented transformation age-at-death distributions proposed by Basellini and Camarda (2020): 3C-STAD

We selected these methods since they represent a wide range of approach in modeling and forecasting mortality, they all model mortality in a single population by single year of age, and routines for estimating these models are freely available (Hyndman et al. 2019; Camarda 2019; Basellini and Camarda 2020).

Nevertheless, it is noteworthy that these approaches have rather different modeling features, rationales and assumptions. Whereas all of them yield future overall mortality patterns, the proposed 3C-sLC is the only (with the exception of the 3C-STAD model) that can provide summary measures as well as age-specific deaths rates over time decomposed in a demographic meaningful manner.

Concerning the data, we used deaths and exposures for five countries: USA, Switzerland (CHE), France (FRA), England and Wales (ENW), and Australia (AUS). We assessed all methods on both males (m) and females (f).

Fig. 9

Poisson deviance residuals of all models for Swiss males. Ages 0–100, fitted years 1960–2018

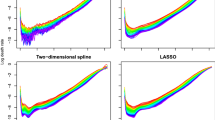
For illustrative purposes, Fig. 9 shows the Poisson deviance residuals of all 5 models for Swiss males. It displays how each model is able to describe observed mortality data over age and time. A good model should show in this plot values about zero (i.e., perfect fit) and without any specific pattern. It is clear that Hyndman–Ullah model and the CP-splines clearly outperform their competitors. However, the 3C-sLC displays smaller residuals than the smooth LC and 3C-STAD model, especially at childhood and early-adult ages. The red and blue clouds (corresponding to model misfit) at ages 20–40 are especially evident for the smooth LC, and they are considerably reduced in the 3C-sLC model.

As for the case of Swiss males, we model all other populations over the period 1960–2018 and we forecast up to 2050. The first three columns in Table 1 present outcomes in terms of model accuracy to observed data. Goodness of fit is measured by deviance (Dev, McCullagh and Nelder 1989), and it is a summary measure for all populations of the residuals shown in Fig. 9 for Swiss males only. The effective dimension (ED) gives a measure of the complexity of the model and the Bayesian information criterion (BIC) balances these two statistics allowing us to evaluate precision in describing the data. With this table, we also aim to emphasize differences in terms of model rigidity. When comparing the ED of the models, it is evident that only 3C-sLC, sLC and CP-S approaches let the data determine the complexity of the estimated model, while the HU and 3C-STAD employ a fixed number of parameters.

In terms of BIC, the CP-S model outperforms all other competitors: the model has indeed high flexibility (a by-product of the P-splines), and the smoothing procedure selects the optimal number of parameters given mortality developments and population size. The second most successful approach is the HU, which employs a larger number of parameters thereby obtaining an excellent fit to the data (the deviance is minimized for all populations). Nonetheless, the use of such a high number of parameters is penalized by the BIC criterion. This is particularly evident for the smallest populations considered (CHE), where the more parsimonious 3C-sLC and 3C-STAD are preferred to the HU model.

In Table 1, we also show the smoothing parameters $\lambda _{\varvec{\alpha }}$ and $\lambda _{\varvec{\beta }}$ employed in fitting the 3C-sLC model for all ten populations. Specifically, in rows associated with 3C-sLC model the two numbers in brackets identify the exponents of the power of ten used as smoothing parameters, e.g., (7, 4) denotes $(\lambda _{\varvec{\alpha }}, \lambda _{\varvec{\beta }}) = (10^7, 10^4)$.

Instead of the conventional long table, we graphically present outcomes based on previous estimations. In particular, Fig. 10 shows life expectancy at birth ($e_{0}$) and average number of life years lost at birth ($e^{\dagger }_{0}$) in 2050 for all 50 combinations of populations and models. As mentioned for both 3C-sLC and 3C-STAD, we are able to decompose these measures in the hypothetical scenarios of removing one or two mortality components from the age-pattern of mortality.

Fig. 10

Forecast life expectancy at birth ($e_0$, top panels) and lifespan disparity ($e^{\dagger }_0$, bottom panels) in 2050 by populations, sex and estimated models. For both 3C-sLC and 3C-STAD models, outcomes are presented also for hypothetical scenarios without the adulthood component, and for the senescence component only. Populations: USA, Switzerland, England and Wales, France and Australia. Models estimated over years 1960–2018, ages 0–100

The 3C-sLC forecasts of $e_{0}$ in 2050 are similar (albeit slightly smaller) to those of the sLC; similar results from the two models emerge in terms of $e^{\dagger }_{0}$, with the 3C-sLC forecasting less compression (i.e., greater disparity) than the sLC. Furthermore, the HU and CP-S generally predict similar or lower levels of $e_{0}$ than the 3C-sLC, while 3C-STAD life expectancy forecasts are generally the most optimistic. In terms of $e^{\dagger }_{0}$, the 3C-STAD and CP-S approaches generally project less compression of the age-at-death distribution in 2050 than the 3C-sLC.

Finally, we assess the forecasting accuracy of the all five models by out-of-sample forecast exercises against the observed trends. We fit all models from 1960 to 2008, and we forecast mortality 10 years ahead (2009–2018), comparing forecast values to those observed over that decade. Table 1 presents these results in terms of life expectancy at birth ($e_{0}$), average number of life years lost at birth ($e^{\dagger }_{0}$) and log-mortality over all ages and years ($\ln \varvec{M}$). We measure the accuracy of the models by computing root mean square error (RMSE) and mean error (ME). Whereas ME describes the forecast bias due to the model, the RMSE assesses the performance of the model on the same units as the measured variable (Chatfield 2000).

From these exercises, it appears that the CP-S produces the most accurate point forecasts, minimizing the two indicators in 20 instances (out of 60). The 3C-STAD is the second most accurate approach with 15 indicators, followed by the HU (11), sLC (10) and 3C-sLC (5).

Table 1 Numerical outcomes from the estimated models as well as for the out-of-sample forecast exercise

Appendix B No Evidence of Adulthood Mortality: The 2C-sLC Model

Whereas the steep mortality decrease during childhood and the exponential increase in the risk of dying from adult ages are generally accepted and evident in all human populations, the presence of an adulthood component can be questionable. As consequence, any mortality model, including the 3C-sLC, attempting to describe an uncertain component may run into identifiability issues. Most importantly, these types of models in these circumstances will be unreasonable from a demographic perspective.

In this appendix, we propose a Two-Component smooth Lee–Carter (2C-sLC) model: a simplification of the proposed approach in which only two components act simultaneously to estimate overall mortality. Again, both components will be described by distinct Lee–Carter models with smooth parameter vectors. Only few adjustments are necessary with respect to what presented in the paper, and two time indexes will be extrapolated for forecasting future mortality.

Computationally more stable with respect to the initial model, this simplified version loses most of the original explanatory value, i.e., whereas a first component will still describe mortality during childhood, the second component will capture all “Residual” mortality.

We estimate this version of the model on Swiss females in which early-adulthood component is not as marked as for males. Figure 11 presents the estimated parameters of the 2C-sLC for Swiss females. As in the original version of the model, average shape of mortality over age, captured by the parameter $\varvec{\alpha }$, is decomposed into two component-specific average patterns. Note that $\varvec{\alpha }_{R}$ for the residual component is sufficiently flexible to capture mortality during early-adulthood which is not exponentially increasing. Component-specific rates of mortality improvements $\varvec{\beta }_k$ and time indexes $\varvec{\kappa }_k$ are presented in central and right panels of Fig. 11, respectively.

Figure 12 shows mortality age-patterns for two selected years (1960 and 2050) with the associated childhood and residual components. The model is able to describe well mortality. The childhood component can be interpreted as in the manuscript, but it is clear that the “Residual” component merges both senescence and early-adulthood mortality features.

Finally, life expectancy over time for both Two- and Three-Component smooth Lee–Carter are portrayed on the right panel of Fig. 12. In terms of overall mortality, both versions of the model provide very similar estimates and differences in future trends are negligible: flexibility of the “Residual” component is so ample to include (and predict) most of the early-adulthood mortality.

Fig. 11

Estimated parameters from 2C-sLC model. Swiss females, ages 0–100, years 1960–2018, time index(es) $\varvec{\kappa }$ forecast up to 2050 by RWD with 80% prediction intervals. Left panel: $\varvec{\alpha }$, average shape of the age profile. Central panel: $\varvec{\beta }$, age-specific average rates of mortality decline. Right panel: $\varvec{\kappa }$, level of mortality at time t. Confidence intervals also computed for the observed years

Fig. 12

Left panel: Observed, fitted and forecast mortality rates (in log scale) in 1960 and 2050. The force of mortality is decomposed into two components (childhood and residual) via the 2C-sLC model. Left panel: Observed, fitted and forecast life expectancy at birth ($e_0$) with 80% prediction intervals obtained by both version of the proposed model. Life expectancy at birth without childhood component is presented for the 2C-sLC model only. Swiss females, ages 0–100, fitted years 1960–2018, forecast years 2019-2050