Skip to main content
SpringerLink
Log in

Thick film flowing down a non-isothermal vertical cylinder

  • Published:
Journal of Engineering Mathematics Aims and scope Submit manuscript

Abstract

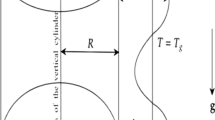
A thick film flow on a non-isothermal vertical cylinder due to gravity is analyzed for temporal and spatiotemporal stability. The model equation is derived by neglecting inertial terms and keeping the full curvature term in the normal stress balance. The thermoviscous and thermocapillary effects are also considered. The film aspect ratio with respect to cylinder radius leads to an increase followed by a decrease in the temporal growth rate. For a cooled substrate, the film can be stabilized for a moderate aspect ratio. Spatiotemporal stability analysis is performed using the Briggs criterion. The aspect ratio significantly affects the spatiotemporal stability of the film. Absolutely unstable regimes are found for small and much larger values of the Bond number, with a convectively unstable regime for moderate values. The critical condition is found that leads to a relation between different model parameters such as Marangoni number, thermoviscosity number, and aspect ratio for which the film is absolutely unstable films for all values of Bond numbers. An opposing pressure gradient is also included in the model through normal stress balance, which can arise due to a counter-current gas flow. While this pressure gradient does not affect the temporal growth rates but promotes absolute instability. Non-linear computations are done to validate the growth rates from both linear temporal and spatiotemporal stability analyses. It is observed that the gaussian disturbance leads to traveling waves well beyond the saturation. The droplet size and gap between two subsequent droplets increase with the gas pressure gradient, thermoviscosity number, and Marangoni number.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13

Similar content being viewed by others

References

  1. Quéré D (1990) Thin films flowing on vertical fibers. EPL (Europhys Lett) 13(8):721

    Article  Google Scholar 

  2. Kliakhandler I, Davis SH, Bankoff S (2001) Viscous beads on vertical fibre. J Fluid Mech 429:381

    Article  MATH  Google Scholar 

  3. Gabbard CT, Bostwick JB (2021) Asymmetric instability in thin-film flow down a fiber. Phys Rev Fluids 6:034005

    Article  Google Scholar 

  4. Craster R, Matar O (2006) On viscous beads flowing down a vertical fibre. J Fluid Mech 553:85

    Article  MathSciNet  MATH  Google Scholar 

  5. Yu L, Hinch J (2014) Drops of power-law fluids falling on a coated vertical fibre. J Fluid Mech 751:184

    Article  MathSciNet  Google Scholar 

  6. Frenkel A (1992) Nonlinear theory of strongly undulating thin films flowing down vertical cylinders. EPL 18(7):583

    Article  Google Scholar 

  7. Kalliadasis S, Chang H-C (1994) Drop formation during coating of vertical fibres. J Fluid Mech 261:135–168

    Article  MATH  Google Scholar 

  8. Khanum S, Tiwari N (2020) Gravity-driven thermoviscous liquid film down a heated or cooled vertical cylinder. Phys Rev Fluids 5(9):094005

    Article  Google Scholar 

  9. Duprat C, Ruyer-Quil C, Kalliadasis S, Giorgiutti-Dauphiné F (2007) Absolute and convective instabilities of a viscous film flowing down a vertical fiber. Phys Rev Lett 98(24):244502

    Article  Google Scholar 

  10. Wray AW, Papageorgiou DT, Matar OK (2017) Reduced models for thick liquid layers with inertia on highly curved substrates. SIAM J Appl Math 77(3):881–904

    Article  MathSciNet  MATH  Google Scholar 

  11. Wray AW, Cimpeanu R (2020) Reduced-order modelling of thick inertial flows around rotating cylinders. J Fluid Mech 898:A1

    Article  MathSciNet  MATH  Google Scholar 

  12. Zeng Z, Sadeghpour A, Warrier G, Ju YS (2017) Experimental study of heat transfer between thin liquid films flowing down a vertical string in the Rayleigh–Plateau instability regime and a counterflowing gas stream. Int J Heat Mass Transf 108:830–840

    Article  Google Scholar 

  13. Chinju H, Uchiyama K, Mori YH (2000) “string-of-beads’’ flow of liquids on vertical wires for gas absorption. AIChE J 46(5):937–945

    Article  Google Scholar 

  14. Ji H, Sadeghpour A, Zeng Z, Ju YS, Bertozzi AL (2019) Dynamics of thin liquid films on vertical cylindrical fibres. J Fluid Mech 865:303–327

    Article  MathSciNet  MATH  Google Scholar 

  15. Binda M, Natali D, Iacchetti A, Sampietro M (2013) Integration of an organic photodetector onto a plastic optical fiber by means of spray coating technique. Adv Mater 25(31):4335–4339

    Article  Google Scholar 

  16. Ding Z, Liu R, Wong TN, Yang C (2018) Absolute instability induced by Marangoni effect in thin liquid film flows on vertical cylindrical surfaces. Chem Eng Sci 177:261–269

    Article  Google Scholar 

  17. Goussis D, Kelly RE (1985) Effects of viscosity variation on the stability of film flow down heated or cooled inclined surfaces: long-wavelength analysis. Phys Fluids 28:3207

    Article  MathSciNet  MATH  Google Scholar 

  18. Srivastava A, Kumawat TC, Tiwari N (2019) Stability analysis of a gravity-driven thermoviscous liquid film flowing over a heated flat substrate. Eur Phys J E 42(5):54

    Article  Google Scholar 

  19. Leslie GA, Wilson S, Duffy B (2012) Thermoviscous coating and rimming flow. Quart J Mech Appl Math 65(4):483–511

    Article  MathSciNet  MATH  Google Scholar 

  20. Leslie GA, Wilson S, Duffy B (2011) Non-isothermal flow of a thin film of fluid with temperature-dependent viscosity on a stationary horizontal cylinder. Phys Fluids 23:062101

    Article  MATH  Google Scholar 

  21. Kumawat TC, Tiwari N (2018) Hydrodynamic stability of thermoviscous liquid film inside a rotating horizontal cylinder: Heating and cooling effects. Phys Fluids 30(3):032103

    Article  Google Scholar 

  22. Wilson S, Duffy B (2003) Strong temperature-dependent-viscosity effects on a rivulet draining down a uniformly heated or cooled slowly varying substrate. Phys Fluids 15(4):827–840

    Article  MathSciNet  MATH  Google Scholar 

  23. Cellier N, Ruyer-Quil C (2020) A new family of reduced models for non-isothermal falling films. Int J Heat Mass Transf 154:119700

    Article  Google Scholar 

  24. Briggs RJ (1964) Electron-stream interaction with plasmas. MIT Press, Cambridge

    Book  Google Scholar 

  25. Kupfer K, Bers A, Ram A (1987) The cusp map in the complex-frequency plane for absolute instabilities. Phys Fluids 30(10):3075–3082

    Article  MathSciNet  Google Scholar 

  26. Huerre P, Monkewitz PA (1990) Local and global instabilities in spatially developing flows. Annu Rev Fluid Mech 22(1):473–537

    Article  MathSciNet  MATH  Google Scholar 

  27. Schmid PJ, Henningson DS (2012) Stability and transition in shear flows, vol 142. Springer Science & Business Media, New York

    MATH  Google Scholar 

  28. Delbende I, Chomaz J-M, Huerre P (1998) Absolute/convective instabilities in the batchelor vortex: a numerical study of the linear impulse response. J Fluid Mech 355:229–254

    Article  MathSciNet  MATH  Google Scholar 

  29. Leber A, Dong C, Chandran R, Gupta TD, Bartolomei N, Sorin F (2020) Soft and stretchable liquid metal transmission lines as distributed probes of multimodal deformations. Nat Electron 3:316–326

    Article  Google Scholar 

Download references

Author information

Author notes

  1. Divij Kishal and Naveen Tiwari contributed equally to this work.

Authors and Affiliations

  1. Department of Chemical Engineering, Indian Institute of Technology Kanpur, Kanpur, Uttar Pradesh, 208016, India

    Divij Kishal & Naveen Tiwari

Authors
  1. Divij Kishal
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Naveen Tiwari
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Naveen Tiwari.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Kishal, D., Tiwari, N. Thick film flowing down a non-isothermal vertical cylinder. J Eng Math 137, 2 (2022). https://doi.org/10.1007/s10665-022-10239-2

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s10665-022-10239-2

Keywords

Search

Navigation