Skip to main content
SpringerLink
Log in

A kernel-free boundary integral method for elliptic PDEs on a doubly connected domain

  • Published:
Journal of Engineering Mathematics Aims and scope Submit manuscript

Abstract

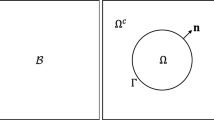
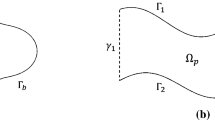
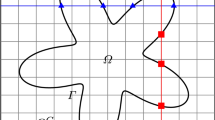
We present a kernel-free boundary integral method (KFBIM) for solving variable coefficients partial differential equations (PDEs) in a doubly connected domain. We focus our study on boundary value problems (BVP) and interface problems. A unique feature of the KFBIM is that the method does not require an analytical form of the Green’s function for designing quadratures but rather computes boundary or volume integrals by solving an equivalent interface problem on Cartesian mesh. We first decompose the problem defined in a doubly connected into two separate interface problems. The system of boundary integral equations is solved using the Krylov method. The method is second-order accurate in space, and its complexity is linearly proportional to the number of mesh points. Numerical examples demonstrate that the method is robust for variable coefficients PDEs, even for cases with large diffusion coefficients ratio and complex geometries where two interfaces are close.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9

Similar content being viewed by others

References

  1. Pozrikidis C (1992) Boundary integral and singularity methods for linearized viscous flow. Cambridge texts in applied mathematics. Cambridge University Press, Cambridge

    Book  Google Scholar 

  2. Sethian J (1996) Level set methods. Cambridge University Press, Cambridge

    MATH  Google Scholar 

  3. Hirt CW, Nichols BD (1981) Volume of fluid (vof) method for the dynamics of free boundaries. J Comput Phys 39(1):201–225

    Article  Google Scholar 

  4. LeVeque RJ, Li ZL (1995) The immersed interface method for elliptic equations with discontinuous coefficients and singular sources. SIAM J Numer Anal 32:1019–1044

    Article  MathSciNet  Google Scholar 

  5. Peskin CS (2002) The immersed boundary method. Acta Numer 11:479

    Article  MathSciNet  Google Scholar 

  6. Ambrose DM, Siegel M, Zhang K (2021) Convergence of the boundary integral method for interfacial stokes flow. arXiv:2105.07056

  7. Hou TY, Lowengrub J, Krasny R (1991) Convergence of a point vortex method for vortex sheets. SIAM J Numer Anal 28(2):308–320

    Article  MathSciNet  Google Scholar 

  8. Hao W, Bei H, Li S, Song L (2018) Convergence of boundary integral method for a free boundary system. J Comput Appl Math 334:128–157

    Article  MathSciNet  Google Scholar 

  9. Greengard L, Rokhlin V (1987) A fast algorithm for particle simulations. J Comput Phys 73:325–348

    Article  MathSciNet  Google Scholar 

  10. Cheng H, Greengard L, Rokhlin V (1999) A fast adaptive multipole algorithm in three dimensions. J Comput Phys 155:468–498

    Article  MathSciNet  Google Scholar 

  11. Liang Z, Gimbutas Z, Greengard L, Huang J, Jiang S (2013) A fast multipole method for the Rotne–Prager–Yamakawa tensor and its applications. J Comput Phys 234:133–139

    Article  MathSciNet  Google Scholar 

  12. Barnes J, Hut P (1986) A hierarchical o(nlogn) force-calculation algorithm. Nature 324:446–449

    Article  Google Scholar 

  13. Lindsay K, Krasny R (2001) A particle method and adaptive treecode for vortex sheet motion in three-dimensional flow. J Comput Phys 172:879–907

    Article  MathSciNet  Google Scholar 

  14. Feng H, Barua A, Li S, Li X (2014) A parallel adaptive treecode algorithm for evolution of elastically stressed solids. Commun Comput Phys 15:365–387

    Article  MathSciNet  Google Scholar 

  15. Ying WJ, Henriquez CS (2007) A kernel-free boundary integral method for elliptic boundary value problems. J Comput Phys 227:1046–1074

    Article  MathSciNet  Google Scholar 

  16. Ying WJ, Wang WC (2013) A kernel-free boundary integral method for implicitly defined surfaces. J Comput Phys 252:606–624

    Article  MathSciNet  Google Scholar 

  17. Mayo A (1984) The fast solution of Poisson’s and the biharmonic equations on irregular regions. SIAM J Numer Anal 21:285–299

    Article  MathSciNet  Google Scholar 

  18. Mayo A (1985) Fast high order accurate solution of Laplace’s equation on irregular regions. SIAM J Sci Statist Comput 6:144–157

    Article  MathSciNet  Google Scholar 

  19. Ying WJ, Wang WC (2014) A kernel-free boundary integral method for variable coefficients elliptic PDES. Commun Comput Phys 15:1108–1140

    Article  MathSciNet  Google Scholar 

  20. Ying W (2018) A cartesian grid-based boundary integral method for an elliptic interface problem on closely packed cells. Commun Comput Phys 24:1196

    Article  MathSciNet  Google Scholar 

  21. Xie Y, Ying W (2019) A fourth-order kernel-free boundary integral method for the modified Helmholtz equation. J Sci Comput 78(3):1632–1658

    Article  MathSciNet  Google Scholar 

  22. Xie Y, Ying W, Wang W-C (2019) A high-order kernel-free boundary integral method for the biharmonic equation on irregular domains. J Sci Comput 80:1681

    Article  MathSciNet  Google Scholar 

  23. Xie Y, Ying W (2020) A high-order kernel-free boundary integral method for incompressible flow equations in two space dimensions. Numer Math Theory Methods Appl 13(3):595–619

    Article  MathSciNet  Google Scholar 

  24. Yaning X, Wenjun Y (2020) A fourth-order kernel-free boundary integral method for implicitly defined surfaces in three space dimensions. J Comput Phys 415:109

    MathSciNet  MATH  Google Scholar 

  25. Shortley GH, Weller R (1938) Numerical solution of Laplace’s equation. J Appl Phys 9:334–348

    Article  Google Scholar 

  26. Cheng LT, Gibou F, Fedkiw F, Kang M (2002) A second-order-accurate symmetric discretization of the Poisson equation on irregular domains. J Comput Phys 176:205–227

    Article  MathSciNet  Google Scholar 

  27. Beeson-Jones TH, Woods AW (2015) On the selection of viscosity to suppress the Saffman–Taylor instability in a radially spreading annulus. J Fluid Mech 782:127–143

    Article  MathSciNet  Google Scholar 

  28. Anjos Pedro HA, Shuwang L (2020) Weakly nonlinear analysis of the Saffman–Taylor problem in a radially spreading fluid annulus. Phys Rev Fluids 5:054002

    Article  Google Scholar 

  29. Zhao M, Anjos Pedro HA, Lowengrub J, Shuwang L (2020) Pattern formation of the three-layer Saffman–Taylor problem in a radial Hele–Shaw cell. Phys Rev Fluids 5:124005

    Article  Google Scholar 

  30. Gin C, Daripa P (2015) Stability results for multi-layer radial Hele–Shaw and porous media flows. Phys Fluids 27:012101

    Article  Google Scholar 

  31. Salameh M, Singh S, Li S, Krishnamurthy M (2020) Surrogate vibration modeling approach for design optimization of electric machines. IEEE Trans Transp Electr 6:1126–1133

    Article  Google Scholar 

  32. Lu M-J, Lowengrub J, Hao W, Li S (2021) Nonlinear simulation of vascular tumor growth with a necrotic core and chemotaxis

  33. Min-Jhe L, Liu C, Lowengrub J, Li S (2020) Complex far-field geometries determine the stability of solid tumor growth with chemotaxis. Bull Math Biol 82:1–41

    MathSciNet  MATH  Google Scholar 

  34. Saad Y, Schultz MH (1986) A generalized minimal residual method for solving non-symmetric linear systems. SIAM J Sci Statist Comput 7:856–869

    Article  MathSciNet  Google Scholar 

  35. Saad Y (1996) Iterative methods for sparse linear systems. PWS Publishing Company, Boston

    MATH  Google Scholar 

  36. Greenbaum A, Greengard L, McFadden GB (1993) Laplace’s equation and the Dirichlet–Neumann map in multiply-connected domains. J Comput Phys 105:267–278

    Article  MathSciNet  Google Scholar 

  37. Beale JT, Layton AT (2006) On the accuracy of finite difference methods for elliptic problems with interfaces. Commun Appl Math Comput Sci 1:91–119

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgements

S. L. and M. K acknowledge the support from the National Science Foundation, Division of Electrical, Communications and Cyber Systems grant ECCS-1927432. S. L. also acknowledges the partial support from the National Science Foundation, Division of Mathematical Sciences grant DMS-1720420. This work is also supported by the National Natural Science Foundation of China (Grant No. DMS-12101553, Grant No. DMS-11771290).

Author information

Authors and Affiliations

  1. Department of Applied Mathematics, Illinois Institute of Technology, Chicago, USA

    Yue Cao & Shuwang Li

  2. College of Science, Zhejiang University of Technology, Xihu, 310023, Hangzhou, People’s Republic of China

    Yaning Xie

  3. Department of Electrical and Computer Engineering, Illinois Institute of Technology, Chicago, USA

    Mahesh Krishnamurthy

  4. School of Mathematical Sciences, MOE-LSC and Institute of Natural Science, Shanghai Jiao Tong University, Shanghai, China

    Wenjun Ying

Authors
  1. Yue Cao
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Yaning Xie
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Mahesh Krishnamurthy
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Shuwang Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Wenjun Ying
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Wenjun Ying.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Cao, Y., Xie, Y., Krishnamurthy, M. et al. A kernel-free boundary integral method for elliptic PDEs on a doubly connected domain. J Eng Math 136, 2 (2022). https://doi.org/10.1007/s10665-022-10233-8

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s10665-022-10233-8

Keywords

Search

Navigation