1 Introduction

The aim of this paper is to contribute some new theoretical results to the rapidly growing literature on the dynamics of insoluble surfactants on free surfaces in the Stokes regime. An important paper by Pozrikidis and Li [1] laid the foundation for much of that literature: in it the authors carried out a numerical investigation of the effects of insoluble surfactants on time-dependent drop deformations in background flows, such as simple shear and extensional flows, at low Reynolds numbers. Many authors have built on that early numerical work [2,3,4,5,6,7,8,9]. The influence of surfactants on steadily-translating bubbles or drops is an especially well-studied problem [5, 10,11,12]. One interesting feature of travelling bubbles in an otherwise quiescent fluid is that surfactants can accumulate at their rear and retard motion [10, 11, 13, 14]. When diffusion is weak, a common phenomenon is the formation of what have become known as stagnant caps [11, 15, 16]. The advection of surfactant to the rear of the rising bubble or drop causes regions of the interface to become immobilized.

Fig. 1
figure 1

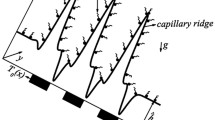
a The problem studied here of surfactant evolution in a linear extensional flow with strain rate \({\dot{\gamma }}_0 >0\) on a deep fluid layer of viscosity \(\mu \) with a free surface at \(y=0\). b It can be viewed as the local “inner” problem in a more complex scenario like the flow at the rear of a rising two-dimensional bubble: a stagnant cap (shown blue) of insoluble surfactant caused by a balance between Marangoni stress and viscous stress from the ambient flow

Full size image

It is with a theoretical description of the formation of stagnant caps that the present paper is concerned. The geometrical set-up is shown in Fig. 1a: a fluid with viscosity \(\mu \) occupies the lower half-plane \(-\infty< x< \infty , y< 0\) with a free capillary surface at \(y=0\) carrying insoluble surfactant with concentration \(\varGamma (x,t)\) determining a surface tension distribution \(\sigma (x,t)\) according to a linear equation of state. In addition, we suppose there is an imposed extensional flow with strain rate \({\dot{\gamma }}_0\). The set-up is a generic one, and is expected to locally describe the formation of a stagnant cap in many situations. For example, as suggested in Fig. 1b, the flow at the rear of a rising gas bubble will look locally—in an “inner” asymptotic sense—akin to this flow arrangement with, in that case, the value of the local strain rate \({\dot{\gamma }}_0\) determined by global features of the flow. The Reynolds number and the capillary number are taken to be zero so that the Stokes equations govern the fluid motion and there is no time-dependent deformation of the free surface. Surface diffusion of the insoluble surfactant is also taken to be negligible. Even with these assumptions, surface advection is still present so the problem remains fully non-linear with a complicated coupling of the bulk fluid motions with the interfacial conditions. Nevertheless, we show here that it is possible to find a class of exact solutions both for the evolution of the surfactant concentration and the induced Marangoni flow in the subphase fluid.

This work can be viewed as a generalization of that by Siegel [16] who, for infinite surface Péclet number, found a class of analytical solutions for equilibria where stagnant caps are located at the two tips of a two-dimensional bubble deformed by an extensional flow such as that produced in the 4-roller-mill experiment of Taylor [17]. The present author has since reappraised those steady solutions involving stagnant caps and generalized them to other geometries [18]. Earlier theoretical work on stagnant caps, including the identification of exact solutions, had been contributed by Sadhal and Johnson [11] for spherical drops also in the low Reynolds number and high Péclet number régime. Siegel [16] used a complex-variable formulation of the two-dimensional problem to find a mathematical description of equilibria involving elongated bubbles with two stagnant caps; he also used his formulation to devise an efficient numerical method to capture the unsteady evolution of the system to those stagnant cap equilibria. In his study, the capillary number is not zero and Siegel tracks the unsteady evolution of the free surface. The new solutions to be presented here generalize Siegel’s results [16] in providing not only an analytical description of the stagnant cap equilibria, but also of their time-dependent formation, albeit in the zero capillary number limit so that there is no free surface deformation as the surfactant evolves.

Our results also generalize prior work on the unsteady spreading of insoluble surfactant over deep water in the Stokes regime [19,20,21,22,23]. An exact “similarity” solution to the two-dimensional problem of a freely spreading strip of insoluble surfactant on deep water was given by [21]. In that solution, weak singularities present in the initial concentration profile persist and evolve in time as the surfactant spreads over the interface; these singularities demarcate the edges of the spreading surfactant zone. The present work extends that solution in two respects: to the case where the surfactant concentration profile is initially regular everywhere on the interface; and to the situation where a countervailing background extensional flow is also present. The background flow changes the solution structure considerably, the most important difference being the possibility of the formation of a stagnant cap equilibrium where the surface concentration profile remains regular at all times and, as shown here explicitly, only tends to a weakly singular one as \(t \rightarrow \infty \). The new solutions of this paper describe the formation of the stagnant cap. They afford us an explicit view of this dynamics as the motion of (square root) branch point singularities evolving in a non-physical region of the complex plane and asymptotically approaching—never actually touching, but drawing exponentially close to—the physical free surface at large times.

The identification of these new exact solutions rests on the observation that, when a linear equation of state relates the surface tension to the surfactant concentration the mathematical problem is equivalent to solving a forced complex Burgers equation for a lower-analytic function with positive real part on the real axis. In this paper, we identify analytical solutions only for infinite surface Péclet number, but other theoretical ramifications of this new connection with the complex Burgers equation, including other exact solutions, for finite surface Péclet number have been surveyed by the author elsewhere [24].

Actually, for infinite surface Péclet number we write down the general solution of the problem in implicit form using a generalized complex “method of characteristics”. To find the exact solutions studied here we restrict attention to a particular class of initial conditions for which this implicit solution can be rendered explicit. In principle, lots more solutions, for other initial conditions, can also be studied within our framework.

Finally, we also show how the effect of first-order reaction kinetics—that is, the evaporation or sublimation of surfactant from the free surface into the upper gas phase—can be incorporated into the mathematical framework and generalized exact solutions found in that case too. The dynamics is then governed by a forced complex Burgers equation with linear damping. The new exact solutions here afford us an explicit view of how reaction effects destroy the stagnant cap equilibrium. It is remarkable that the dynamics of a non-linear multiphysics system incorporating surface advection of surfactant, forcing by a background extensional flow, and reaction kinetics can all be captured in a mathematically explicit way.

2 Marangoni flow on deep viscous fluid

The Stokes equations governing the flow in \(y < 0\) in Fig. 1a are

$$\begin{aligned} \mu \nabla ^2 \mathbf{u} = \nabla p, \qquad {\nabla .\mathbf{u}} = 0, \end{aligned}$$
(1)

where p(x, y, t) is the fluid pressure. The far-field strain in the lower half-plane is taken to be

$$\begin{aligned} (u,v) \sim (-{{\dot{\gamma }}_0} x, {{\dot{\gamma }}_0} y) \qquad \mathrm{as}~ |z| \rightarrow \infty , \end{aligned}$$
(2)

where \({\dot{\gamma }}_0\) is the strain rate. The upper half region \(y >0\) is occupied by an inviscid gas at constant pressure \(p_\mathrm{g}\). On a general two-dimensional interface, the stress induced by the non-uniform surface tension \(\sigma (s,t)\), say, where s denotes arc-length along the boundary taken such that s increases with the fluid region on the left, must be balanced by the interfacial fluid stress [16, 18, 25, 26]:

$$\begin{aligned}{}[\mathbf{T}. \mathbf{n}]^\mathrm{fluid}_\mathrm{gas} = \sigma \kappa \mathbf{n} - {\varvec{\nabla }}_\mathrm{s} \sigma , \qquad \mathbf{T} \equiv -p \mathbf{I} + \mu \left[ {\varvec{\nabla }} \mathbf{u} + ({\varvec{\nabla }} \mathbf{u})^\mathrm{T} \right] , \end{aligned}$$
(3)

where \(\mathbf{T}\) is the fluid stress tensor in either phase, \([\mathbf{T}. \mathbf{n}]^\mathrm{fluid}_\mathrm{gas}\) denotes the jump in the bracketed quantity between its limit approached from the fluid side and from the gas side, \(\kappa \) is the curvature of the surface and \(\nabla _\mathrm{s} = (\mathbf{I} - \mathbf{n} \mathbf{n}).\nabla \) denotes the surface gradient on the interface having unit normal \(\mathbf{n}\) directed into the fluid. The tangential projection of the boundary condition (3) along the interface gives the Marangoni stress balance

$$\begin{aligned} \mu \mathbf{t}.\left[ {\varvec{\nabla }} \mathbf{u} + ({\varvec{\nabla }} \mathbf{u})^\mathrm{T} \right] .\mathbf{n} = - {\partial \sigma \over \partial s}. \end{aligned}$$
(4)

In the particular case shown in Fig. 1, the interface is flat, we can take \(s=-x\) with \(z=x\) so that \(\mathrm{d}z/\mathrm{d}s=-1\) on the interface.

For dilute concentrations of insoluble surfactant it is satisfactory to assume a linear equation of state

$$\begin{aligned} \sigma (x,t)= \sigma _0 - {\beta \varGamma (x,t)}, \end{aligned}$$
(5)

where \(\sigma _0\) is the clean-flow surface tension, \(\varGamma (x,t)\) is the local surfactant concentration and \(\beta = RT > 0\) is a non-dimensional parameter governing the sensitivity of the surface tension to changes in the surfactant concentration here R is the gas constant and T is the absolute temperature. The surfactant evolution equation [27] on \(y=0\) for \(\varGamma (x,t)\) is

$$\begin{aligned} {\partial \varGamma (x,t) \over \partial t} + {\partial (U(x,t) \varGamma (x,t) ) \over \partial x} = D_\mathrm{s} {\partial ^2 \varGamma (x,t) \over \partial x^2}, \end{aligned}$$
(6)

where \(D_\mathrm{s}\) is the surface diffusion coefficient and U(x, t) is the surface slip velocity. The ratio of viscous diffusion to surface diffusion is taken to be large so that the advective non-linearity in (6) will control the dynamics and induce a quasi-steady Stokes flow in the bulk.

Let L be a typical length scale set, say, by the initial distribution of surfactant placed on the surface and let \(\varGamma _0\) be a characteristic surfactant level. We will introduce the velocity scale defined by

$$\begin{aligned} U_0 = {\beta \varGamma _0 \over 2\mu }. \end{aligned}$$
(7)

If a capillary number based on the clean-flow surface tension is defined to be \(\mathrm{Ca} = {\mu U_0 / \sigma _0}\) it can be shown [25] by an analysis of the normal projection of (3) along the interface that as \(\mathrm{Ca} \rightarrow 0\) it is consistent to seek a solution for a flat meniscus where \(p_0 = p_\mathrm{g}\), here \(p_\mathrm{g}\) is the uniform gas pressure in \(y >0\) and \(p_0\) denotes the average surface pressure of the fluid in \(y< 0\). The justification is set out in an appendix to [25] where the fluid pressure is conveniently decomposed as \(p=p_0+P(x,y,t)\) where P(x, y, t) is the deviation from \(p_0\). It is shown there that, for a flat, zero-curvature interface, the pressure \(p_0\) must balance the ambient gas pressure \(p_\mathrm{g}\).

In summary, in the zero capillary number limit \(\mathrm{Ca} \rightarrow 0\), the interface \(y=0\) is a streamline of the flow with the Marangoni stress balance (4) holding on it. These are the boundary conditions needed to solve for the Stokes flow in the lower half-plane.

3 Complex variable formulation

In this section, it is convenient to retain dimensional variables. The quasi-steady Stokes flow in \(y< 0\) is describable by a biharmonic streamfunction \(\psi (z,{\overline{z}},t)\) associated with incompressible subphase flow (u, v) given by [16, 18, 25, 28]

$$\begin{aligned} \psi (z,{\overline{z}},t) = \mathrm{Im}[{\overline{z}}f(z,t) + g(z,t)], \qquad (u,v) = \left( {\partial \psi \over \partial y}, -{\partial \psi \over \partial x} \right) , \end{aligned}$$
(8)

where f(z, t) and g(z, t) are two functions of \(z =x + \mathrm{i} y\) analytic in the lower half-plane, except at infinity and possibly on the free surface \(y=0\). It can be shown [16, 18, 25] that the fluid pressure P, the vorticity \(\omega = -\nabla ^2 \psi \) and the fluid rate-of-strain tensor \(e_{ij}=(1/2)(\partial u_i/\partial x_j + \partial u_j/\partial x_i)\) are related to f(z, t) and g(z, t) through

$$\begin{aligned} \begin{aligned}&4 f'(z,t) = {P \over \mu } - \mathrm{i} \omega , \qquad u - \mathrm{i} v = - \overline{f(z,t)} + {\overline{z}} {f'(z,t)} + {g'(z,t)} , \\&e_{11} + \mathrm{i} e_{12} = z \overline{f''(z,t)} + \overline{g''(z,t)}, \end{aligned} \end{aligned}$$
(9)

where primes denote differentiation with respect to z. There is an additive degree of freedom in the choice of f(z, t) and \(g'(z,t)\) since the transformations \(f(z,t) \mapsto f(z,t) + c\) and \(g'(z,t) \mapsto g'(z,t) + {\overline{c}}\), where c is a complex constant, do not affect the complex velocity field \(u-\mathrm{i}v\) given in (9). This degree of freedom will be specified shortly.

On inspection of (8) it can be checked that the choice

$$\begin{aligned} g(z,t) = - z f(z,t) \end{aligned}$$
(10)

ensures that \(\psi =0\) on \(y=0\), where \({\overline{z}} = z\), and renders it a streamline. This choice also turns out to be consistent with the far-field requirements. It also constrains the additive constant c to be purely imaginary. The complex velocity field, with g(z, t) given by (10), is

$$\begin{aligned} u - \mathrm{i} v = - \overline{f(z,t)} + {\overline{z}} {f'(z,t)} + {g'(z,t)} = - \overline{f(z,t) }+ ({\overline{z}}- z) f'(z,t) -{f(z,t)}. \end{aligned}$$
(11)

On \(y=0\), where \({\overline{z}} = z = x\), it is found from (11) that

$$\begin{aligned} u-\mathrm{i} v = U(x,t) = - f(z,t) - \overline{f(z,t)} = -2\, \mathrm{Re}[f(z,t)]. \end{aligned}$$
(12)

The author has shown elsewhere [25] that the complex form of the total stress exerted by the fluid on the boundary is

$$\begin{aligned} -2 \mu \mathrm{i} {\partial H \over \partial s}, \qquad H(z, {\overline{z}},t) = f(z,t) + z \overline{f'(z,t)} + \overline{g'(z,t)}, \end{aligned}$$
(13)

where we have used the fact that the complex form of the unit tangent is \(\mathrm{d}z/\mathrm{d}s\) with the corresponding complex unit normal vector directed into the fluid given by \(\mathrm{i}\, \mathrm{d}z/\mathrm{d}s\). The complex form of the tangential stress condition on the meniscus is therefore

$$\begin{aligned} \mathrm{Re} \left[ \overline{\mathrm{d}z \over \mathrm{d}s} \left( -2 \mu \mathrm{i} {\partial H \over \partial s} \right) \right] = - {\partial \sigma \over \partial s}, \qquad y=0. \end{aligned}$$
(14)

Recalling that, for the present problem, \(s=-x\), then (14) and (5) imply

$$\begin{aligned} \mathrm{Re} \left[ 2 \mu \mathrm{i} {\partial H \over \partial x} \right] = - {\partial \sigma \over \partial x} = \beta {\partial \varGamma (x,t) \over \partial x} \qquad \mathrm{on}~y=0. \end{aligned}$$
(15)

Condition (15) can be integrated with respect to x on \(y=0\):

$$\begin{aligned} \mathrm{Im}[2 \mu H]= - \beta \varGamma (x,t) + c_\infty (t) \qquad \mathrm{on}~y=0, \end{aligned}$$
(16)

where \(c_\infty (t)\) is some real-valued function of time. On use of (10), it can be checked that

$$\begin{aligned} H = f(x,t) -\overline{f(x,t)} = 2\mathrm{i}\, \mathrm{Im}[f(x,t)] \qquad \mathrm{on} ~~y=0. \end{aligned}$$
(17)

Therefore, combining (16) and (17), on \(y=0\) it is found that

$$\begin{aligned} \mathrm{Im}[f(x,t)]= - {\beta \over 4 \mu }\varGamma (x,t) \qquad \mathrm{on}~y=0, \end{aligned}$$
(18)

where we have set \(c_\infty (t)=0\) using an aforementioned additive degree of freedom in the choice of f(z, t). It follows from (12) and (18) that

$$\begin{aligned} f(x,t) = - {U(x,t) \over 2} - {\mathrm{i} \over 4 \mu } \beta \varGamma (x,t) \qquad \mathrm{on}~y=0. \end{aligned}$$
(19)

As \(x \rightarrow \pm \infty \)   on \(y=0\),

$$\begin{aligned} U(x,t) \rightarrow - {\dot{\gamma }}_0 x + {{\mathcal {O}}}(1/x), \qquad \varGamma (x,t) \rightarrow 0. \end{aligned}$$
(20)

It is therefore necessary that

$$\begin{aligned} f(z,t) \rightarrow {{\dot{\gamma }}_0 z \over 2} + {{\mathcal {O}}}(1/z) \qquad \mathrm{as}~ |z| \rightarrow \infty . \end{aligned}$$
(21)

4 The forced complex Burgers equation

The following mathematical arguments have been set out in detail recently by the author in [24] but the key steps will be repeated here since the derivation of the new solutions relies crucially on these observations. Suppose that lengths are non-dimensionalized with respect to L, velocities with respect to \(U_0\), time with respect to \(L/U_0\) and \(\varGamma \) with respect to a typical surfactant level \(\varGamma _0\) then the surfactant evolution equation [27] on \(y=0\) can be written

$$\begin{aligned} {\partial \varGamma (x,t) \over \partial t} + {\partial (U(x,t) \varGamma (x,t) ) \over \partial x} = {1 \over \mathrm{Pe}_\mathrm{s}} {\partial ^2 \varGamma (x,t) \over \partial x^2} \qquad \mathrm{on}~y=0, \end{aligned}$$
(22)

where \(\mathrm{Pe}_\mathrm{s} = U_0 L/D_\mathrm{s}\) is the surface Péclet number and it is understood that all quantities now refer to their non-dimensional counterparts.

It is convenient to introduce the non-dimensional analytic function h(z, t) defined by

$$\begin{aligned} f(z,t) = - {U_0 \over 2} h(z,t), \end{aligned}$$
(23)

where, on \(y=0\), it follows from (19) that

$$\begin{aligned} h(x,t) = {U(x,t)} + {\mathrm{i} \varGamma (x,t) } \qquad \mathrm{on}~y=0. \end{aligned}$$
(24)

A crucial observation is that U(x, t) and \(\varGamma (x,t)\) appear as the real and imaginary parts of a lower-analytic function h(z, t) evaluated on the boundary \(y=0\) of the lower half-plane. The far-field conditions, following from (20) and (21), require that

$$\begin{aligned} h(z,t) \rightarrow -{\dot{\gamma }} z + {{\mathcal {O}}}(1/z), \end{aligned}$$
(25)

where

$$\begin{aligned} {\dot{\gamma }} = {L \over U_0} {\dot{\gamma }}_0 \end{aligned}$$
(26)

is the non-dimensionalized strain rate. It follows on squaring the definition (24) that

$$\begin{aligned} h(x,t)^2 = {U(x,t)}^2 - \varGamma (x,t)^2 + 2{\mathrm{i} U(x,t) \varGamma (x,t) }. \end{aligned}$$
(27)

From (24) and (27), (22) can be written as

$$\begin{aligned} \mathrm{Im} \left[ {\partial h(z,t) \over \partial t} + {\partial \over \partial z} \left( {h(z,t)^2 \over 2} \right) - {1 \over \mathrm{Pe}_\mathrm{s}} {\partial ^2 h(z,t) \over \partial z^2} \right] = 0 \qquad \mathrm{on}~y=0. \end{aligned}$$
(28)

A key observation is that, with the far-field behaviour (25), the function in square brackets in (28) is a lower-analytic function with a simple pole of known strength at infinity. Moreover, (28) says that its imaginary part vanishes on \(y=0\). By analytic continuation off \(y=0\), we infer that

$$\begin{aligned} {\partial h(z,t) \over \partial t} + {\partial \over \partial z} \left( {h(z,t)^2 \over 2} \right) - {1 \over \mathrm{Pe}_\mathrm{s}} {\partial ^2 h(z,t) \over \partial z^2} = {{\dot{\gamma }}}^2 z, \end{aligned}$$
(29)

where the function on the right-hand side of (29) is also lower analytic with the same known far-field behaviour as the left-hand side, and with vanishing imaginary part on \(y=0\). A possible real constant on the right-hand side of (29) has been omitted in order to be consistent with the left-hand side when (25) holds.

Equation (29) is the forced complex Burgers equation. When \({{\dot{\gamma }}}=0\), so that the background strain is absent, (29) is the usual complex viscous Burgers equation for the lower-analytic function h(z, t) with the inverse surface Peclet number \(1/\mathrm{Pe}_\mathrm{s}\) playing the role of viscosity. This observation has many important theoretical ramifications explored in detail by the author elsewhere [24]. For the remainder of this paper we consider only the case \(\mathrm{Pe}_\mathrm{s} \rightarrow \infty \). This means that surface diffusion of surfactant is neglected. We retain, however, the challenging non-linear advection terms in the surfactant evolution equation.

Remark

The connection—given recently by the author in [24] and reviewed above—between the complex Burgers equation and insoluble surfactant evolution on the undeformed surface of deep water in the Stokes regime with a linear equation of state appears to have been missed by all previous authors (even without any imposed background strain). This connection is shown in [24] to lead to a linearization of the full non-linear problem, via a transformation of Cole–Hopf type, even at finite surface Péclet number. Harper [19] studied a similar Stokes flow problem using a formulation based on analytic functions akin to ours but only considered a steady flow situation with no time dependence. It is also recognized [21,22,23] that, in the flow set-up considered here, the surface slip U(x, t) and surfactant concentration \(\varGamma (x,t)\) are related by a Hilbert transform. That fact makes it natural, as we have done, to consider the evolution of a lower-analytic function h(z, t) but besides Harper [19], who exploited the theory of analytic functions in his steady flow analysis, no other previous authors appear to have explored the problem this way.

5 Steady stagnant cap solution

In the limit \(\mathrm{Pe}_\mathrm{s} \rightarrow \infty \) a solution of the steady version of (29), namely,

$$\begin{aligned} h(z,t) {\partial \over \partial z} h(z,t) = {{\dot{\gamma }}}^2 z, \end{aligned}$$
(30)

is easily found to be the time-independent function

$$\begin{aligned} h_{\text {SC}}(z;a) \equiv - {{\dot{\gamma }}} (z^2-a^2)^{1/2}, \qquad a \in {\mathbb {R}}^+, \end{aligned}$$
(31)

where the subscript “SC” reflects the fact that (31) corresponds to a “stagnant cap” equilibrium. As \(|z| \rightarrow \infty \), this solution satisfies

$$\begin{aligned} h_{\text {SC}}(z;a) \sim - {{\dot{\gamma }}} z, \end{aligned}$$
(32)

ensuring that (25) is satisfied, and is otherwise analytic in the lower half-plane. The function \(h_{\text {SC}}(z;a)\) is not analytic on the real axis though: it has two square root branch points at \(x = \pm a\). These are the edges of the stagnant cap. Using the notation \(h_{\text {SC}}(x;a) = U_{\text {SC}}(x;a)+ \mathrm{i} \varGamma _{\text {SC}}(x;a)\) we see that on the interface when \(|x| > a\),

$$\begin{aligned} U_{\text {SC}}(x;a) = \left\{ \begin{array}{rr} {{\dot{\gamma }}} (x^2-a^2)^{1/2}, &{} ~x > a, \\ -{{\dot{\gamma }}} (x^2-a^2)^{1/2}, &{} ~x < a, \end{array} \right. \qquad \varGamma _{\text {SC}}(x;a)= 0 \end{aligned}$$
(33)

implying that there is no surfactant outside the interval \((-a,a)\), while for \(|x| < a\),

$$\begin{aligned} U_{\text {SC}}(x;a) = 0, \qquad \varGamma _{\text {SC}}(x;a)= {{\dot{\gamma }}} (a^2-x^2)^{1/2} \end{aligned}$$
(34)

meaning that the interval \((-a,a)\) is a stagnant cap—a free surface region which is immobile and occupied by surfactant. The singularities at \((\pm a,0)\) are weak in the sense that both the slip velocity and surfactant distribution are continuous there while it is easy to confirm, from (31), (23) and (9), that the fluid stress is singular but integrable. A simple integration leads to

$$\begin{aligned} \int _{-a/2}^{a/2} \varGamma _{\text {SC}}(x;a) \mathrm{d}x = {{\dot{\gamma }} a^2 \pi \over 2}, \end{aligned}$$
(35)

reflecting the total amount of surfactant in the cap.

6 General solution to the unsteady problem

In the limit \(\mathrm{Pe}_\mathrm{s} \rightarrow \infty \), (29) becomes

$$\begin{aligned} {\partial h(z,t) \over \partial t} + {\partial \over \partial z} \left( {h(z,t)^2 \over 2} \right) = {{\dot{\gamma }}}^2 z. \end{aligned}$$
(36)

Remarkably, an implicit form of the general solution of the non-linear partial differential equation (36) can be found. First, let

$$\begin{aligned} h(z,t) = -{{\dot{\gamma }}} z + k(z,t), \end{aligned}$$
(37)

where \(k(z,t) \rightarrow 0\) as \(|z| \rightarrow \infty \). On substitution of (37) into (36), the modified partial differential equation for k(z, t) is

$$\begin{aligned} {\partial k(z,t) \over \partial t} + (k(z,t) -{{\dot{\gamma }}} z) {\partial k(z,t) \over \partial z} = {{\dot{\gamma }}} k(z,t). \end{aligned}$$
(38)

Given a suitable initial condition k(z, 0) this can be formally solved by (a complex version of) the method of characteristics. The method is procedurally the same as the traditional method. Based on (38) we can say that

$$\begin{aligned} {\mathrm{d}k \over \mathrm{d}t} = {{\dot{\gamma }}} k(z,t) \end{aligned}$$
(39)

on complex characteristics defined by the equation

$$\begin{aligned} {\mathrm{d} z \over \mathrm{d}t} = k(z,t)-{{\dot{\gamma }}} z, \end{aligned}$$
(40)

where we set \(z=Z\) when \(t=0\). In this way, Z serves as a label of the characteristics. On use of an integrating factor in (39),

$$\begin{aligned} \mathrm{e}^{-{{\dot{\gamma }}} t} k(z,t) = K(Z), \qquad K(Z) =k(Z,0). \end{aligned}$$
(41)

Relation (41) implies that \(\mathrm{e}^{-{{\dot{\gamma }}} t} k(z,t)\) is constant on characteristics those being determined by

$$\begin{aligned} {\mathrm{d} \over \mathrm{d}t} (\mathrm{e}^{{{\dot{\gamma }}} t} z) =\mathrm{e}^{ {{\dot{\gamma }}} t} k(z,t) = \mathrm{e}^{2 {{\dot{\gamma }}} t} K(Z). \end{aligned}$$
(42)

The first equation follows from (40) after use of a suitable integrating factor; the second equality in (42) has made use of (41). Equation (42) can now be integrated with respect to t:

$$\begin{aligned} \mathrm{e}^{{{\dot{\gamma }}} t} z = K(Z) r(t) + Z, \end{aligned}$$
(43)

where it is useful to introduce the function of time defined by

$$\begin{aligned} r(t) \equiv {\mathrm{e}^{2 {{\dot{\gamma }}} t} - 1 \over 2 {{\dot{\gamma }}}}. \end{aligned}$$
(44)

An implicit form of the general solution to (38) is therefore

$$\begin{aligned} k(z,t) = K(Z)\mathrm{e}^{{{\dot{\gamma }}} t}, \qquad \mathrm{e}^{{{\dot{\gamma }}} t} z = K(Z) r(t) + Z, \qquad K(z) = k(z,0). \end{aligned}$$
(45)

Having such an expression for the general solution to this non-linear problem is already valuable. Rather than explore all its ramifications here, however, we have chosen to focus on showing how it can be used to derive a class of exact solutions by taking particular choices of initial condition for which the implicit general solution (45) can be made explicit.

7 A class of explicit solutions

Consider the 3-parameter family of initial conditions

$$\begin{aligned} k(z,0) = c \left[ (z-\mathrm{i}B) - ((z-\mathrm{i}B)^2-a^2)^{1/2} \right] , \qquad c, a, B \in {\mathbb {R}}^+. \end{aligned}$$
(46)

This function is analytic in the lower half-plane and has two square root branch point singularities at \(\pm a + \mathrm{i} B\) which are in the (non-physical) upper half-plane provided that \(B > 0\); if \(B=0\), these singularities are on the physical free surface, but this is a special case that will be discussed again later. The initial choice (46) also satisfies the required condition that \(k(z,0) \rightarrow 0\) as \(|z| \rightarrow \infty \) for any choice of c, a and B. On taking the limit \(a \rightarrow 0\) and \(c \rightarrow \infty \) while fixing the quantity

$$\begin{aligned} A = {c a^2 \over 2} \end{aligned}$$
(47)

the initial condition (46) tends to the rational function

$$\begin{aligned} k(z,0) = {A \over z- \mathrm{i} B}, \qquad A , B \in {\mathbb {R}}^+. \end{aligned}$$
(48)

This observation is useful because it allows us to deduce that

$$\begin{aligned} {\varGamma (x,0)} = \mathrm{Im}[h(z,0)] = \mathrm{Im}[k(z,0)] = {AB \over x^2+B^2} \qquad \mathrm{on}~y=0, \end{aligned}$$
(49)

which, being strictly positive for all x, is a physically admissible initial condition for the surfactant concentration which must be non-negative everywhere on the interface on physical grounds. We therefore expect the same to be true of the more general initial condition (46) for which this feature is checked a posteriori.

Use of (46) in (45) gives the implicit form of the solution as

$$\begin{aligned} \begin{aligned} k(z,t)&= c \left[ (Z-\mathrm{i}B) - ((Z-\mathrm{i}B)^2-a^2)^{1/2} \right] \mathrm{e}^{{{\dot{\gamma }}} t}, \\ \mathrm{e}^{{{\dot{\gamma }}} t} z&= c \left[ (Z-\mathrm{i}B) - ((Z-\mathrm{i}B)^2-a^2)^{1/2} \right] r(t) + Z. \end{aligned} \end{aligned}$$
(50)

The key to rendering these solutions explicit is to notice that, on introducing \({{\mathcal {Z}}} = {{\mathcal {Z}}}(z,t)= Z-\mathrm{i}B\), the second equation in (50) can be rearranged to

$$\begin{aligned} c r(t) ({{\mathcal {Z}}}^2-a^2)^{1/2} = (c r(t)+1) {{\mathcal {Z}}} - (\mathrm{e}^{{{\dot{\gamma }}} t} z- \mathrm{i}B) \end{aligned}$$
(51)

which, on squaring, leads to

$$\begin{aligned} (2 c r(t) + 1){{\mathcal {Z}}}^2 - 2 (c r(t)+1) (\mathrm{e}^{{{\dot{\gamma }}} t}z -\mathrm{i}B) {{\mathcal {Z}}} + (\mathrm{e}^{{{\dot{\gamma }}} t} z -\mathrm{i}B)^2 + (c r(t) a)^2 =0. \end{aligned}$$
(52)

This quadratic equation for \({{\mathcal {Z}}}(z,t)\) is readily solved to give

$$\begin{aligned} {{\mathcal {Z}}}(z,t)= {\mathrm{e}^{{{\dot{\gamma }}} t} (z-\mathrm{i} B \mathrm{e}^{-{{\dot{\gamma }}} t})\over 2 c r(t) +1} \left[ c r(t)+1 + c r(t) \left[ 1-\left( {\xi (t) \over z-\mathrm{i} B \mathrm{e}^{-{{\dot{\gamma }}} t}} \right) ^2 \right] ^{1/2} \right] , \end{aligned}$$
(53)

where

$$\begin{aligned} \xi (t)^2 = (2 c r(t)+1) a^2 \mathrm{e}^{-2 {{\dot{\gamma }}} t}, \end{aligned}$$
(54)

and where we have written this in a functional form that is most convenient for numerical evaluation. From (50) the solution for k(z, t) is then

$$\begin{aligned} k(z,t) = c {{\mathcal {Z}}}(z,t) \left[ 1 - \left( 1-\left( {a \over {{\mathcal {Z}}}(z,t)}\right) ^2 \right) ^{1/2} \right] \mathrm{e}^{{{\dot{\gamma }}} t}, \end{aligned}$$
(55)

which, on back substitution into (37), gives h(z, t) as

$$\begin{aligned} h(z,t) = - {\dot{\gamma }} z + c {{\mathcal {Z}}}(z,t) \left[ 1 - \left( 1-\left( {a \over {{\mathcal {Z}}}(z,t)}\right) ^2 \right) ^{1/2} \right] \mathrm{e}^{{{\dot{\gamma }}} t}, \end{aligned}$$
(56)

which is an explicit expression because (53) furnishes a formula for \({{\mathcal {Z}}}(z,t)\).

This solution tends, at large times, to the stagnant cap equilibrium. To see this, note that as \(t \rightarrow \infty \),

$$\begin{aligned} r(t) \rightarrow {\mathrm{e}^{2 {{\dot{\gamma }}} t} \over 2 {{\dot{\gamma }}}}, \qquad \xi (t)^2 \rightarrow {c a^2 \over {{\dot{\gamma }}}}, \qquad {{\mathcal {Z}}}(z,t) \rightarrow {\mathrm{e}^{{{\dot{\gamma }}} t} \over 2} \left[ z + (z^2-c a^2/{{\dot{\gamma }}})^{1/2} \right] \end{aligned}$$
(57)

implying that

$$\begin{aligned} k(z,t) = c \mathrm{e}^{{{\dot{\gamma }}} t} {{\mathcal {Z}}}(z,t) \left[ 1 - \left( 1-\left( {a \over {{\mathcal {Z}}}(z,t)}\right) ^2 \right) ^{1/2} \right] \rightarrow {a^2 c \mathrm{e}^{{{\dot{\gamma }}} t} \over 2{{\mathcal {Z}}}(z,t)} \end{aligned}$$
(58)

hence, from (57),

$$\begin{aligned} k(z,t) \rightarrow {a^2 c \mathrm{e}^{{{\dot{\gamma }}} t} \over \mathrm{e}^{{{\dot{\gamma }}} t} z + \mathrm{e}^{{{\dot{\gamma }}} t} (z^2-c a^2/{{\dot{\gamma }}})^{1/2} } = {{\dot{\gamma }}} \left( z - (z^2-c a^2/{{\dot{\gamma }}})^{1/2} \right) \end{aligned}$$
(59)

and therefore, from (37),

$$\begin{aligned} h(z,t) = - {{\dot{\gamma }}} z + k(z,t) \rightarrow -{{\dot{\gamma }}} \left( z^2-{c a^2 \over {{\dot{\gamma }}}} \right) ^{1/2} = h_{\text {SC}}(z;\sqrt{c a^2/{{\dot{\gamma }}}}) \end{aligned}$$
(60)

which is the steady stagnant cap solution.

If the background strain is turned off by setting \({\dot{\gamma }}=0\), and the special choice \(B=0\) is made, then the solution just found retrieves the weakly singular spreading solution of Thess [21] which he derived using a very different method. The new solutions above generalize that solution to a class of non-singular solutions when \(B >0\) since the two branch points of the initial data are then strictly in the non-physical upper half-plane (and not on the real axis). The derivation of the \(B=0\) solution in [21] involves posing an ansatz dependent on two unknown time-evolving functions and solving a pair of ordinary differential equations for those functions arising as consistency conditions in the surfactant evolution equation (6).

It should be clear that the general implicit form of the solution (45) of the complex Burgers equation (29) with \({\dot{\gamma }}=0\) provides a route to deriving many other solutions of the pure spreading problem. It would be interesting to explore whether the implicit expression (45) can be made explicit for any other choices of initial data.

Figure 2 shows a typical time evolution of the surfactant concentration \(\varGamma (x,t) = \mathrm{Im}[h(x,t)]\) with h(x, t) given by (56). The chosen parameters are \({\dot{\gamma }}=1, B=0.01, a=0.5\) and \(c=2/a^2\) so, from (60), the long-time stagnant cap equilibrium to which the solution evolves is \(h_{\text {SC}}(x;\sqrt{2})\). The surfactant concentration is smooth initially, and remains so at all subsequent times. This solution demonstrates the unsteady spreading of an initially compact layer of surfactant to a broader stagnant cap profile. As seen from (53) the solution has two time-evolving square root branch points in the upper half-complex plane at

$$\begin{aligned} \pm \xi (t) + \mathrm{i} B \mathrm{e}^{-{\dot{\gamma }} t}, \end{aligned}$$
(61)

which at long times become exponentially close to the two points

$$\begin{aligned} \lim _{t \rightarrow \infty } \pm \xi (t) = \pm a \sqrt{c \over {\dot{\gamma }}} \end{aligned}$$
(62)

on the real axis which are the precisely square root branch points at the edges of the stagnant cap solution (60). The singularities never actually reach the real axis in finite time, however. It may also appear, from (56), that h(z, t) also has square root branch points associated with points where \({{\mathcal {Z}}}(z,t)=\pm a\) but it can be verified that these are removable singularities.

Fig. 2
figure 2

Unsteady spreading of an initially compact layer of surfactant towards a broader stagnant cap as \(t \rightarrow \infty \) for \({\dot{\gamma }}=1, B=0.01, a=0.5\) and \(c=2/a^2\). \(\varGamma (x,t)\) and U(x, t) approach a stagnant cap occupying the interval \((-\sqrt{c a^2/{{\dot{\gamma }}}} ,\sqrt{c a^2/{{\dot{\gamma }}}})\) or \((-\sqrt{2}, \sqrt{2})\) in this case. Snapshots shown at \(t=0,0.2,0.4,0.6,0.8\) & 2

Full size image
Fig. 3
figure 3

Unsteady sweeping together, or compactifying, of an initially dispersed surfactant layer towards a stagnant cap as \(t \rightarrow \infty \) for \({\dot{\gamma }}=1, B=2, a=1\) and \(c=2\). \(\varGamma (x,t)\) and U(x, t) approach a stagnant cap occupying the interval \((-\sqrt{c a^2/{{\dot{\gamma }}}} ,\sqrt{c a^2/{{\dot{\gamma }}}})\) or \((-\sqrt{2}, \sqrt{2})\) in this case. Snapshots shown at \(t=0,1,2,3,4,8\)

Full size image

Figure 3 shows the opposite scenario: the time evolution of a compactifying distribution of surfactant which is initially more spread out than the eventual stagnant cap equilibrium to which it tends. The chosen parameters are \({\dot{\gamma }}=1, B=2, a=1\) and \(c=2/a^2\) so that the large-time stagnant cap equilibrium is the same as in Fig. 2, i.e. \(h_{\text {SC}}(x;\sqrt{2})\). Again, two square root singularities in the non-physical upper half-plane draw exponentially close to the real axis as \(t \rightarrow \infty \) but they do not reach it in finite time.

In this infinite surface Péclet number limit there is no obstruction to setting \(B=0\), in which case the initial condition is itself (weakly) singular with two branch points at \(\pm \xi (0) = \pm a\) and these are preserved under the evolution and move on the real axis. The solutions found above are then precisely the generalizations of the spreading solutions of [21, 22] to the case \({\dot{\gamma }} \ne 0\) where a background extensional flow is present. As \(t \rightarrow \infty \) the solution also tends to the stagnant cap solution (60) whose branch points are at \(\pm a \sqrt{c/{{\dot{\gamma }}}}\). In this case, it is easy to determine a priori whether solutions will be spreading or compactifying: they correspond to \({c/{{\dot{\gamma }}}} > 1\) and \({c/{{\dot{\gamma }}}} < 1\), respectively. The critical choice \(c/{{\dot{\gamma }}}=1\) with \(B=0\) is the stagnant cap equilibrium itself. From these considerations, it is clear how the class of solutions above with \(B > 0\) regularizes these singular \(B=0\) solutions.

8 The effect of reaction kinetics on the stagnant cap equilibrium

It turns out that the effect of first-order reaction kinetics can be incorporated into the framework we have developed without sacrificing the mathematical features that have led to the identification of exact solutions for infinite surface Péclet number. Consequently, we are able to find generalized exact solutions for surfactant dynamics in the presence of both background extensional flows and reaction kinetics. The word “reaction” is used here to capture mechanisms such as sublimation or evaporation of the fluid-insoluble surfactants off the interface to the upper ambient gas phase. The effect of reaction kinetics is important: previous authors [13] have examined their implications for the stagnant cap dynamics and rise velocity of bubbles when the Reynolds number is large. They are also important for replenishing surface tension gradients relied upon for the purposes of the so-called viscous Marangoni propulsion [26].

With the addition of a reaction term that removes surfactant from the interface at a rate proportional to its local concentration, the non-dimensional surfactant evolution equation becomes

$$\begin{aligned} {\partial \varGamma (x,t) \over \partial t} + {\partial (U(x,t) \varGamma (x,t) ) \over \partial x} = {1 \over \mathrm{Pe}_\mathrm{s}} {\partial ^2 \varGamma (x,t) \over \partial x^2} - \alpha \varGamma (x,t), \end{aligned}$$
(63)

where \(\alpha > 0\) is the non-dimensionalized reaction rate at which surfactant sublimates to the upper gas phase. The important observation is that the new reaction term appearing last in (63) can again be identified as the imaginary part of a lower-analytic function meaning that this generalized surfactant evolution equation is also the imaginary part of a lower-analytic function. After analytic continuation arguments akin to those outlined earlier, it can be shown that the evolution equation for the lower-analytic function h(z, t) becomes

$$\begin{aligned} {\partial h(z,t) \over \partial t} + h(z,t) {\partial h(z,t) \over \partial z} - {1 \over \mathrm{Pe}_\mathrm{s}} {\partial ^2 h(z,t) \over \partial z^2} + \alpha h(z,t) = -{{\dot{\gamma }}} z (\alpha - {\dot{\gamma }}). \end{aligned}$$
(64)

When \(\alpha =0\) this reduces to Eq. (29) as expected.

When \(\alpha \ne 0\) and \({\dot{\gamma }}=0\) the partial differential equation (64) is the complex Burgers equation with linear damping.

When \(\alpha \ne 0\) and \({\dot{\gamma }} \ne 0\) (64) might be described as a forced complex Burgers equation with linear damping.

Equation (64) will now be solved in the limit \(\mathrm{Pe}_\mathrm{s} \rightarrow \infty \). Again it is convenient to write

$$\begin{aligned} h(z,t) = - {\dot{\gamma }} z + k(z,t), \end{aligned}$$
(65)

where

$$\begin{aligned} k(z,t) \sim {{\mathcal {O}}}(1/z) \qquad \mathrm{as}~ |z| \rightarrow \infty . \end{aligned}$$
(66)

On substitution of (65) into (64), we find the modified partial differential equation

$$\begin{aligned} {\partial k(z,t) \over \partial t} + (k(z,t)-{\dot{\gamma }} z) {\partial \over \partial z} k(z,t) = ( {\dot{\gamma }} -\alpha ) k(z,t). \end{aligned}$$
(67)

The method of characteristics used earlier leads to the following implicit form of the general solution:

$$\begin{aligned} k(z,t)= K(Z)\mathrm{e}^{({\dot{\gamma }}-\alpha )t} \qquad Z = \mathrm{e}^{{\dot{\gamma }} t} z - K(Z) r(t), \qquad K(z) = k(z,0), \end{aligned}$$
(68)

where now the relevant function of time is

$$\begin{aligned} r(t) \equiv \left\{ \begin{array}{ll} \displaystyle {\mathrm{e}^{(2 {\dot{\gamma }} -\alpha )t}-1 \over 2 {\dot{\gamma }} -\alpha }, &{} ~~\alpha \ne 2 {\dot{\gamma }}, \\ ~ &{} ~ \\ t, &{} ~~\alpha = 2 {\dot{\gamma }}. \end{array} \right. \end{aligned}$$
(69)

While (68) is an implicit expression of the general solution, we can again generate a class of explicit solutions by choosing an initial condition within the 3-parameter family (46) used in the absence of reaction effects. An alternative, to be studied here, is to choose the 2-parameter family of initial conditions

$$\begin{aligned} K(z) = k(z,0) = {A \over z-\mathrm{i}B}, \qquad A > 0, ~B \ge 0. \end{aligned}$$
(70)

It was shown in Sect. 7 how this 2-parameter set of initial conditions emerges, in the double limit \(a \rightarrow 0\) and \(c \rightarrow \infty \) with A fixed according to (47), of the 3-parameter family (68). The real parameter A must be positive to ensure a non-negative surfactant concentration everywhere on the interface; moreover, for \(B >0\) this initial data is non-singular on the interface and the associated h(z, 0) is lower analytic, as required. We find, using (70) in (68) and on substitution into (65), that the solution for \(t>0\) is

$$\begin{aligned} \begin{aligned} h(z,t) = -{\dot{\gamma }} z + {\mathrm{e}^{(2 {\dot{\gamma }}-\alpha ) t} (z- \mathrm{i} B\mathrm{e}^{-{\dot{\gamma }} t}) \over 2 r(t)}&\biggl [ 1 - \left( 1 - {\eta (t)^2 \over (z- \mathrm{i} B\mathrm{e}^{-{\dot{\gamma }} t})^2} \right) ^{1/2} \biggr ], \end{aligned} \end{aligned}$$
(71)

where

$$\begin{aligned} \eta (t)^2 \equiv 4 A \mathrm{e}^{-2 {\dot{\gamma }} t} r(t) = \left\{ \begin{array}{ll} {{4A \over 2 {\dot{\gamma }} -\alpha } (\mathrm{e}^{-\alpha t} - \mathrm{e}^{-2 {\dot{\gamma }} t})}, &{}~~~ \alpha \ne 2 {\dot{\gamma }}, \\ ~ &{} ~ \\ 4 A \mathrm{e}^{-2 {\dot{\gamma }} t} t, &{}~~~ \alpha = 2 {\dot{\gamma }}. \end{array} \right. \end{aligned}$$
(72)

This is an explicit class of exact solutions valid for any positive \(\alpha \) and \({\dot{\gamma }}\). From the viewpoint of evolving complex singularities, the initial simple pole of h(z, 0) in the upper half-plane at \(\mathrm{i} B\) becomes, for \(t > 0\), two moving square root branch points of h(z, t) at

$$\begin{aligned} \pm \eta (t) + \mathrm{i} B \mathrm{e}^{-{\dot{\gamma }} t}. \end{aligned}$$
(73)

These remain in the upper half-plane for all \(t > 0\) but note the interesting long-time behaviour of their real parts:

$$\begin{aligned} \lim _{t \rightarrow \infty } \pm \eta (t) = \left\{ \begin{array}{ll} \pm \sqrt{2A/{\dot{\gamma }}} , &{} ~~\alpha = 0, {\dot{\gamma }} \ne 0, \\ \pm \sqrt{4A/\alpha } , &{} ~~\alpha \ne 0, {\dot{\gamma }} = 0, \\ 0, &{} ~~\alpha \ne 0, {\dot{\gamma }} \ne 0. \\ \end{array} \right. \end{aligned}$$
(74)

It is useful to survey how the class of solutions (71) reduces, for special choices of the parameters, to other known results in three cases. This helps to show how (71) both unifies, and generalizes, those more restricted results.

Case 1: We can turn off the background strain, \({\dot{\gamma }}=0\), and the reaction effects, \(\alpha =0\), and also select \(B=0\) in the initial condition. Such solutions are initially weakly singular on the free surface, and remain so for \(t > 0\), but they are still admissible in the \(\mathrm{Pe}_\mathrm{s} \rightarrow \infty \) limit. Indeed, it can then be checked that (71) retrieves the (weakly singular) pure spreading solutions found by previous authors [21, 22]. Generalized solutions within this class, e.g. for \(B > 0\), have been examined by the author in [24].

Case 2: If only background strain is turned off, \({\dot{\gamma }}=0\), then, again for the special initial condition \(B=0\), (71) becomes

$$\begin{aligned} h(z,t) ={{\mathcal {A}}}(t) \left[ z - \left( z^2 - \xi (t)^2 \right) ^{1/2} \right] , \end{aligned}$$
(75)

where

$$\begin{aligned} r_B(t) \equiv {1- \mathrm{e}^{-\alpha t} \over \alpha }, \qquad {{\mathcal {A}}}(t) = {\mathrm{e}^{-\alpha t} \over 2 r_B(t)}, \qquad \xi (t)^2 = 4 A r_B(t). \end{aligned}$$
(76)

Since \(B=0\) these solutions are again initially weakly singular on the free surface, and remain so for \(t > 0\), and we retrieve solutions recently reported by Bickel [29] who proceeded very differently, as discussed below. The corresponding surfactant concentration is

$$\begin{aligned} \varGamma (x,t) ={{\mathcal {A}}}(t) \sqrt{\xi (t)^2-x^2}. \end{aligned}$$
(77)

Our solution corresponds to Bickel’s for the particular choice of initial conditions \(\xi (0) \rightarrow 0, {{\mathcal {A}}}(0) \rightarrow \infty \) with \({{\mathcal {A}}}(0)\xi (0)^2 = 2A\). Although they did not arise in our derivation (nor are they needed) it is easily verified from the explicit expressions (76) that \(\xi (t)\) and \({{\mathcal {A}}}(t)\) satisfy the ordinary differential equations

$$\begin{aligned} {\mathrm{d} \xi \over \mathrm{d}t} = \xi {{\mathcal {A}}}(t), \qquad {\mathrm{d}{{\mathcal {A}}} \over \mathrm{d}t} + 2 {{\mathcal {A}}}^2 + \alpha {{\mathcal {A}}} =0 \end{aligned}$$
(78)

determined by Bickel [29]. Indeed, he derived (78) by emulating Thess’s approach [22] of assuming the functional ansatz (77) and showed that if \(\xi (t)\) and \({{\mathcal {A}}}(t)\) evolve according to (78) then (77) is a solution for the evolving surfactant concentration. Our solution scheme is very different: here this same solution emerges as a special case of a more general solution found here using a complexified method of characteristics applied to a forced complex Burgers equation with linear damping. Even with no background extensional flow \({\dot{\gamma }}=0\), the new class of solutions (71) generalizes that of Bickel [29] to a class which for \(B> 0\) are regular everywhere on the interface, including at \(t=0\). In the limit \(t \rightarrow \infty \) the solution (75) becomes trivial owing to the exponential decay of the amplitude prefactor function \({{\mathcal {A}}}(t)\) even though the branch points tend to distinct points on the real axis as already noted in (74).

Case 3: If, on the other hand, the reaction effects are switched off, \(\alpha =0\), then (71) becomes

$$\begin{aligned} h(z,t) = - {\dot{\gamma }} z + {\mathrm{e}^{2 {\dot{\gamma }} t} (z- \mathrm{i} B\mathrm{e}^{-{\dot{\gamma }} t} )\over 2 r_{\text {SC}}(t)} \left[ 1 - \left( 1 - {4 A \mathrm{e}^{-2 {\dot{\gamma }} t} r_{\text {SC}}(t) \over (z- \mathrm{i} B\mathrm{e}^{-{\dot{\gamma }} t} )^2} \right) ^{1/2} \right] , \end{aligned}$$
(79)

where

$$\begin{aligned} r_{\text {SC}}(t) \equiv {\mathrm{e}^{2 {\dot{\gamma }} t}-1 \over 2 {\dot{\gamma }} }. \end{aligned}$$
(80)

It can be checked that this is the limit, as \(a \rightarrow 0\) and \(c \rightarrow \infty \) with A fixed according to (47), of the solution (56) obtained earlier. In the long-time limit \(t \rightarrow \infty \) this solution tends to the stagnant cap equilibrium:

$$\begin{aligned} h(z,t) \rightarrow h_{\text {SC}}(z; \sqrt{2A/{\dot{\gamma }}}) \equiv - {\dot{\gamma }} (z^2- 2A/{\dot{\gamma }})^{1/2}. \end{aligned}$$
(81)

In contrast to what happens in the presence of reaction effects, there is no amplitude decay in this case and the non-trivial stagnant cap equilibrium is reached.

With these three special cases surveyed, it is clear that the new generalized exact solutions (71) afford the opportunity to examine in detail how first-order reaction affects the evolution to the stagnant cap equilibrium (81). It is found that reaction effects destroy the possibility of equilibrium, at least for this chosen class of initial conditions and this is expected to be the case more generally.

While the stagnant cap equilibrium is destroyed, the balance between the reaction rate and the background strain rate is critical to determining the nature of the resulting surfactant dynamics. The dynamics are now characterized by a competition between two time scales: one associated with the strain rate of the background extensional flow, another set by the reaction rate of the surface kinetics. Signs of this physical competition are already evident from the motion of the branch points encapsulated in (72), (73) and (74): indeed, the crossover “resonant” value \(\alpha = 2 {\dot{\gamma }}\) is precisely the case where both effects are equally important to the dynamics causing the algebraic rather than the exponential time dependence evident in (72).

Figure 4 shows a time sequence of the (rescaled) interfacial surfactant distribution \( \varGamma (x,t)\) and surface slip U(x, t) as functions of x. The parameter values chosen are \({\dot{\gamma }}=1, \alpha =0.1, A=B=0.1\) so that reaction effects are relatively weak compared to the background strain. Since \(B> 0\) the initial condition, and the solution for all \(t > 0\), is regular everywhere on the interface. The solution approaches a stagnant cap equilibrium but does not quite reach it: the reaction effects, while weak, have eliminated the possibility of equilibrium. The system remains in a state of “near-equilibrium” for an extended period before eventually decaying at larger times. This is manifested by the gradual shrinking in the width of a nearly stagnant cap.

Fig. 4
figure 4

Slow reaction: evolution of \(\varGamma (x,t)\) and U(x, t) for \({\dot{\gamma }}=1, \alpha =0.1, A=B=0.1\) and \(t=0, 0.5, 1, 5, 10, 20\). A nearly stagnant cap forms but gradually shrinks to zero width due to sublimation of the surfactant to the upper gas phase

Full size image

Figure 5 shows a time sequence of the same initial state when the reaction rate has increased, \(\alpha =1\), so that it is now comparable to the ambient strain rate. Although the system again appears to approach a stagnant cap equilibrium, it is now only a glancing approach and the spread, or “variance” in the language of [29], of the surfactant zone now dies off much more quickly due to reaction effects. Further calculations show that, at even higher reaction rates, the surfactant sublimates off the interface so quickly that the system never gets close to any near-equilibrium resembling a stagnant cap.

Fig. 5
figure 5

Moderate reaction: evolution of \(\varGamma (x,t)\) and U(x, t) for \({\dot{\gamma }}= \alpha =1, A=B=0.1\) and \(t=0, 0.1, 0.5, 1, 2, 4\). A nearly stagnant zone appears but it shrinks in size as time evolves

Full size image

9 Discussion

This paper has shown that the non-linear interplay between viscous Marangoni effects, surface advection of surfactant, an ambient extensional flow and first-order reaction kinetics can be captured analytically by a class of explicit time-evolving solutions relevant at zero Reynolds and capillary numbers, and at infinite surface Péclet number. Indeed, the general solution has also been written down, albeit implicitly, in (65) and (68) and those formulas offer a promising route to a numerical approach to this class of problems even when explicit solutions are not available.

The 3-parameter family of solutions found here when reaction effects are absent but a linear extensional flow is present provide useful benchmarks exhibiting, in a mathematically explicit way, the unsteady formation of stagnant caps at infinite surface Péclet number. For \(B>0\) the initial surfactant concentration is smooth, and in the solutions here remains smooth for all time. Depending on initial parameter choices, the solutions exhibit either the spreading or compactifying of the initial surfactant distribution to the stagnant cap equilibrium. As \(t \rightarrow \infty \) the solutions get exponentially close to the stagnant cap equilibrium and this can now be understood mathematically as the motion of complex singularities in an unphysical region of the complex plane. Indeed, two square root branch points approach the interface from the non-physical upper half-plane where, if they were to actually hit the axis, would form the edges of the stagnant cap. When \(B=0\) those square root branch points already exist in the initial data, and the solutions here then describe the evolution of the edges of an evolving cap (or “zone” of surfactant) to those of the steady stagnant cap. Understanding free surface Stokes flow problems via the motion of singularities in a non-physical complex plane has already provided a valuable theoretical viewpoint in other contexts [28, 30, 31].

Although not observed in the solutions examined here, without surface diffusion one might reasonably expect the formation of finite-time singularities for other choices of initial condition and this deserves much further investigation. Indeed, the formation, at finite time, of a weak singularity for an initially smooth surfactant distribution has been observed [24] in this system when the background flow and the reaction effects are absent (\({\dot{\gamma }} = \alpha = 0\)). That singularity is associated with the presence of an initial isolated “clean point” on an otherwise surfactant-contaminated interface, this causes an evolving square root branch point in the unphysical upper half-plane to hit the real axis in finite time at which point the graphs of both \(\varGamma (x,t)\) and U(x, t) simultaneously develop infinite slope as functions of x. The solution does not break down at this weak singularity, however, and the offending branch point only touches the real axis and immediately turns back into the upper half-plane; see [24] for more details. It is likely that similar weak singularities, or perhaps other types such as surfactant shocks [32], also occur in the presence of background flows and reaction kinetics. This is to be explored in future work.

Our new theoretical understanding of this Marangoni problem in terms of the forced complex Burgers equation with linear damping for the lower-analytic function h(z, t) offers promise for other new results even at finite surface Péclet number [24]. The author [24] has already explored some of the implications for Marangoni flows of a Cole–Hopf-type transformation familiar from other problems where the Burgers equation arises. It is important to emphasize that this Cole–Hopf transformation linearizes the problem for any surface Péclet number [24], a mathematical observation with far-reaching consequences.

The explicit nature of the new solutions should make them useful as the basis of studies where additional physical effects are introduced, perhaps within a perturbative framework. They should also serve as valuable benchmarks for numerical codes aimed at resolving flow in more complex geometries and with additional physical effects. The effects on this solution class of solubility to the bulk, more general sorption kinetics, non-zero Reynolds number effects, and the influence of surface diffusion are just a few things of interest. Another generalization of the approach is to time-varying far-field strain where the background strain rate becomes time dependent.

Finally, as suggested schematically in Fig. 1b, the solutions may also be useful as the inner solution in a matched asymptotic analysis of a more geometrically complicated unsteady problem such as the evolution of the rear stagnant caps of a rising bubble [11, 15].