Abstract
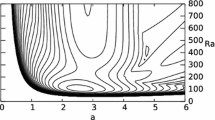
Energy stability theory is applied to the study of the nonlinear stability of natural convection in an inclined fluid layer having a uniform internal heat source (sink), with the boundaries of the layer maintained at constant temperatures. The stability limit is found in terms of the thermal Rayleigh number \(R_{1}\) and the internal Rayleigh number \(R_{2}\). The region of stability is found in \(R_{1}\)–\(R_{2}\) plane where the base state is stable against arbitrary perturbations. The Prandtl number Pr of the fluid and the angle of inclination of the fluid layer play an important role in determining the stability region.








Similar content being viewed by others
References
B\({\breve{e}}\)hounkov\(\acute{\text{a}}\) M, Tobie G, Choblet G, \(\breve{C}\)adek O (2010) Coupling mantle convection and tidal dissipation: applications to enceladus and earth-like planets. J Geophys Res 115(E9):2156–2202
Spiegel EA (1971) Convection in stars I. Basic Boussinesq convection. Annu Rev Astron Astrophys 9(1):323–352
Grötzbach G, Wörner M (1999) Direct numerical and large eddy simulations in nuclear applications. Int J Heat Fluid Flow 20(3):222–240
Tveitereid M (1978) Thermal convection in a horizontal fluid layer with internal heat sources. Int J Heat Mass Transf 21(3):335–339
Tritton DJ, Zarraga MN (1967) Convection in horizontal layers with internal heat generation. Experiments. J Fluid Mech 30(1):21–31
Kulacki FA, Goldstein RJ (1972) Thermal convection in a horizontal fluid layer with uniform volumetric energy sources. J Fluid Mech 55(2):271–287
Roberts PH (1967) Convection in horizontal layers with internal heat generation theory. J Fluid Mech 30(1):33–49
Goluskin D (2016) Internally heated convection and Rayleigh–Bénard convection. Springer, New York
Gershuni GZ, Zhukhovitskii EM, Yakimov AA (1970) On the stability of steady convective motion generated by internal heat sources: Pmm vol. 34, n=4, 1970, pp. 700-705. J Appl Math Mech 34(4):669–674
Takashima M (1983) The stability of natural convection in a vertical fluid layer with internal heat generation. J Phys Soc Jpn 52(7):2364–2370
Takashima M, Hamabata H (1985) The stability of natural convection in a vertical fluid layer having side walls of different temperatures and internal heat generation. J Phys Soc Jpn 54(5):1782–1788
Gershuni GZ, Zhukhovitsky EM, Iakimov AA (1974) On stability of plane-parallel convective motion due to internal heat sources. Int J Heat Mass Transf 17(7):717–726
Takashima M (1989) The stability of natural convection in an inclined fluid layer with internal heat generation. J Phys Soc Jpn 58(12):4431–4440
Takashima M (1990) The stability of natural convection due to internal heat sources in a vertical fluid layer. Fluid Dyn Res 6(1):15–23
Saravanan S, Brindha D (2011) Global nonlinear stability of convection in a heat generating fluid filled channel with a moving boundary. Appl Math Lett 24(4):487–493
Sahu KC (2011) The Instability of flow through a slowly diverging pipe with viscous heating. J Fluids Eng 133(7):071201
Gautam K, Narayana PAL (2019) On the stability of carbon sequestration in an anisotropic horizontal porous layer with a first-order chemical reaction. Proc R Soc A 475(2226):20180365
Govindarajan R, Sahu KC (2014) Instabilities in viscosity-stratified flow. Annu Rev Fluid Mech 46(1):331–353
Reddy VK, Janardhanan VM, Sahu KC (2011) Effects of wall-heating on the linear instability characteristics of pressure-driven two-layer channel flow. Chem Eng Sci 66(23):6272–6279
Hideo I (1984) Experimental study of natural convection in an inclined air layer. Int J Heat Mass Transf 27(8):1127–1139
Lee JH, Goldstein RJ (1988) An experimental study on natural convection heat transfer in an inclined square enclosure containing internal energy sources. J Heat Transf 110(2):345–349
Hill AA (2005) Double-diffusive convection in a porous medium with a concentration based internal heat source. Proc R Soc A 461(2054):561–574
Kumar G, Narayana PAL, Sahu KC (2020) Linear and nonlinear thermosolutal instabilities in an inclined porous layer. Proc R Soc A 476(2233):20190705
Storesletten L, Rees DAS (2019) Onset of convection in an inclined anisotropic porous layer with internal heat generation. Fluids 4(2):75
Joseph DD (1966) Nonlinear stability of the Boussinesq equations by the method of energy. Arch Ration Mech Anal 22(3):163–184
Joseph DD (1976) Stability of fluid motions I, vol 27. Springer, New York
Arora M, Singh J, Bajaj R (2020) Nonlinear stability of natural convection in an inclined fluid layer. Int J Appl Comput Math 6(21):1–15
Arora M, Bajaj R (2020) Stability of transient natural convection in impulsively heated inclined fluid layer. Fluid Dyn Res 52(5):055501
Chandrasekhar S (1961) Hydrodynamic and hydromagnetic stability. Oxford University Press, Oxford
Galdi GP, Straughan B (1985) Exchange of stabilities, symmetry, and nonlinear stability. Arch Ration Mech Anal 89(3):211–228
Straughan B (1992) The energy method, stability, and nonlinear convection, vol 91. Springer, Berlin
Acknowledgements
The authors are thankful to the reviewers for their valuable comments which resulted in the improvement of the manuscript. Financial aid from the University Grants Commission (UGC), New Delhi, through Grant No F.16-6(DEC.2016)2017(NET) (403462) to Manisha Arora in the form of Senior Research Fellowship is gratefully acknowledged.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflicts of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Arora, M., Bajaj, R. Global stability of natural convection in internally heated inclined fluid layer. J Eng Math 128, 7 (2021). https://doi.org/10.1007/s10665-021-10127-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10665-021-10127-1