Skip to main content
SpringerLink
Log in

Postbuckling analysis of a nonlinear beam with axial functionally graded material

  • Published:
Journal of Engineering Mathematics Aims and scope Submit manuscript

Abstract

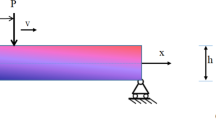
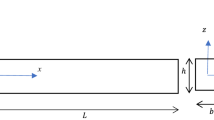
The postbuckling analysis of a modified nonlinear beam composed of axial functionally graded material (FGM) is investigated by a canonical dual finite element method (CD-FEM). The governing equation of the axial FGM nonlinear beam is derived through a variational method. The CD-FEM is adopted to find the nonconvex postbuckling configurations of the beam according to Gao’s triality theory. Using duality transition, the original potential energy functional becomes a functional of deformation and dual stress fields. By variation of the mixed complementary energy, the coupling equations are derived to find deformation and dual stress fields. In FEM, matrices of a beam element depend on the gradient of material property (elastic modulus). To obtain general forms of matrices of a beam element, the graded elastic modulus is approximated by piecewise linear functions with respect to axial position. Numerical examples are presented to show the effects of graded elasticity on the postbuckling configurations of the beam.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18

Similar content being viewed by others

References

  1. Suresh S, Mortensen A (1988) Fundamentals of functionally graded materials. IOM Communications, London

    Google Scholar 

  2. Jha DK, Kant T, Singh RK (2013) A critical review of recent research on functionally graded plates. Compos Struct 96:833–849

    Article  Google Scholar 

  3. Wang H, Qin QH, Kang YL (2006) A meshless model for transient heat conduction in functionally graded materials. Comput Mech 38:51–60

    Article  MATH  Google Scholar 

  4. Wang H, Qin QH (2008) Meshless approach for thermo-mechanical analysis of functionally graded materials. Eng Anal Boundary Elements 32:704–712

    Article  MATH  Google Scholar 

  5. Wang H, Qin QH (2012) Boundary integral based graded element for elastic analysis of 2d functionally graded plates. Eur J Mech A Solids 33:12–23

    Article  MathSciNet  Google Scholar 

  6. Eltaher MA, Emam SA, Mahmoud FF (2013) Static and stability analysis of nonlocal functionally graded nanobeams. Compos Struct 96:82–88

    Article  Google Scholar 

  7. Chakraborty A, Gopalakrishnan S (2003) A spectrally formulated finite element for wave propagation analysis in functionally graded beams. Int J Solids Struct 40:2421–2448

    Article  MATH  Google Scholar 

  8. Yang J, Chen Y (2008) Free vibration and buckling analyses of functionally graded beams with edge cracks. Compos Struct 83:48–60

    Article  Google Scholar 

  9. Simsek M (2010) Vibration analysis of a functionally graded beam under a moving mass by using different beam theories. Compos Struct 92:904–917

    Article  Google Scholar 

  10. Huang Y, Li X-F (2010) A new approach for free vibration of axially functionally graded beams with non-uniform cross-section. J Sound Vib 329:2291–2303

    Article  ADS  Google Scholar 

  11. Reddy JN (2011) Microstructure-dependent couple stress theories of functionally graded beams. J Mech Phys Solids 59:2382–2399

    Article  ADS  MATH  MathSciNet  Google Scholar 

  12. Ke L-L, Yang J, Kitipornchai S (2009) Postbuckling analysis of edge cracked functionally graded timoshenko beams under end shortening. Compos Struct 90:152–160

    Article  Google Scholar 

  13. Singh KV, Li G (2009) Buckling of functionally graded and elastically restrained non-uniform columns. Compos Part B Eng 40:393–403

    Article  Google Scholar 

  14. Benatta MA, Tounsi A, Mechab I, Bouiadjra MB (2009) Mathematical solution for bending of short hybrid composite beams with variable fibers spacing. Appl Math Comput 212:337–348

    Article  MATH  MathSciNet  Google Scholar 

  15. Sharifishourabi G, Alebrahim R, Teshnizi SHS, Ani FN (2012) Effects of material gradation on thermo-mechanical stresses in functionally graded beams. In: Dan Y (ed) 2nd international conference on chemistry and chemical process, pp. 194–199

  16. Murin J, Aminbaghai M, Hrabovsky J, Kutis V, Kugler S (2013) Modal analysis of the fgm beams with effect of the shear correction function. Compos Part B Eng 45:1575–1582

    Article  Google Scholar 

  17. Shahba A, Attarnejad R, Hajilar S (2011) Free vibration and stability of axially functionally graded tapered Euler–Bernoulli beams. Shock Vib 18:683–696

    Article  Google Scholar 

  18. Gao DY (1996) Nonlinear elastic beam theory with application in contact problems and variational approaches. Mech Res Commun 23:11–17

    Article  MATH  Google Scholar 

  19. Gao DY (2000) Duality principles in nonconvex systems: theory, methods and applications. Kluwer Academic Publishers, Dordrecht

    Book  Google Scholar 

  20. Kuttler KL, Purcell J, Shillor M (2012) Analysis and simulations of a contact problem for a nonlinear dynamic beam with a crack. Q J Mech Appl Math 65:1–25

    Article  MATH  MathSciNet  Google Scholar 

  21. Lu CF, Chen WQ, Xu RQ, Lim CW (2008) Semi-analytical elasticity solutions for bi-directional functionally graded beams. Int J Solids Struct 45:258–275

    Article  Google Scholar 

  22. Levinson M (1965) Complementary energy theorem in finite elasticity. J Appl Mech 32:826–828

    Article  MathSciNet  Google Scholar 

  23. Qin QH (1995) Geometrically nonlinear analysis of shells by the variational approach and an efficient finite element formulation. Comput Struct 55:727–733

    Article  ADS  MATH  Google Scholar 

  24. Qin QH (1995) Postbuckling analysis of thin plates by a hybrid trefftz finite element method. Comput Methods Appl Mech Eng 128:123–136

    Article  ADS  MATH  Google Scholar 

  25. Gao Y, Strang G (1989) Geometric nonlinearity: potential-energy, complementary energy, and the gap function. Q Appl Math 47:487–504

    MATH  MathSciNet  Google Scholar 

  26. Gao DY (1999) Pure complementary energy principle and triality theory in finite elasticity. Mech Res Commun 26:31–37

    Article  MATH  Google Scholar 

  27. Gao DY (1999) General analytic solutions and complementary variational principles for large deformation nonsmooth mechanics. Meccanica 34:169–198

    MATH  MathSciNet  Google Scholar 

  28. Li SF, Gupta A (2006) On dual configurational forces. J Elast 84:13–31

    Article  MATH  MathSciNet  Google Scholar 

  29. Pian THH (1964) Derivation of element stiffness matrices by assumed stress distributions. AIAA J 2:1333–1336

    Article  Google Scholar 

  30. Hodge PG, Belytsch T (1968) Numerical methods for limit analysis plates. J Appl Mech 35:796–801

    Article  MATH  Google Scholar 

  31. Qin QH (2000) The trefftz finite and boundary element method. WIT Press, Southampton

    MATH  Google Scholar 

  32. Qin QH (2003) Variational formulations for TFEM of piezoelectricity. Int J Solids Struct 40:6335–6346

    Article  MATH  Google Scholar 

  33. Qin QH, Wang H (2008) Matlab and C programming for trefftz finite element methods. Taylor and Francis, Boca Raton

    Book  Google Scholar 

  34. Jirousek J, Wroblewski A, Qin QH, He XQ (1995) A family of quadrilateral hybrid Trefftz p-element for thick plate analysis. Comput Methods Appl Mech Eng 127:315–344

    Google Scholar 

  35. Gao DY, Wu C (2012) On the triality theory for a quartic polynomial optimization problem. J Ind Manag Optim 8:229–242

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgments

The financial support of the US Air Force Office of Scientific Research (Grant No. FA9550-10-1-0487), the National Natural Science Foundation of China (Grant No. 50908190), the Youth Talents Foundation of Shaanxi Province (Grant No. 2011kjxx02), and the Research Foundation (GZ1205) of the State Key Laboratory of Structural Analysis for Industrial Equipment, Dalian University of Technology, Dalian, China, is fully acknowledged.

Author information

Authors and Affiliations

  1. College of Water Resources and Architectural Engineering, Northwest A&F University, Yangling , 712100, China

    Kun Cai

  2. School of Science, Information Technology and Engineering, University of Ballarat, Mt Helen, VIC , 3353, Australia

    David Y. Gao

  3. Research School of Engineering, Australia National University, Canberra, ACT , 0200, Australia

    David Y. Gao & Qing H. Qin

Authors
  1. Kun Cai
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. David Y. Gao
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Qing H. Qin
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Qing H. Qin.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Cai, K., Gao, D.Y. & Qin, Q.H. Postbuckling analysis of a nonlinear beam with axial functionally graded material. J Eng Math 88, 121–136 (2014). https://doi.org/10.1007/s10665-013-9682-1

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10665-013-9682-1

Keywords

Search

Navigation