Analysis of oblique wave interaction with a submerged perforated semicircular breakwater

Abstract

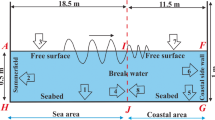
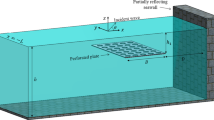
This study examines oblique wave interaction with a submerged perforated semicircular breakwater based on the linear potential theory. The fluid domain is divided into inner and outer regions by a perforated semicircular arc. The velocity potentials in the inner and outer regions are constructed by eigenfunction expansions and multipole expansions, respectively. The unknown constants in the velocity potentials are determined by matching the boundary conditions on the perforated arc. The convergence of the solution method we have developed is rapid. The reflection and transmission coefficients and the wave forces acting on the breakwater are calculated and examined. Some useful results are presented for practical engineering.

Appendix: Multipoles with singularities on the water bottom for oblique wave

Multipoles with singularities on the water bottom were given by Chapman [9]. Here the symmetric and antisymmetric multipoles, which have singularities at the semicircular breakwater centre $r$ $=$ 0 and satisfy Eqs. (3)–(6), are briefly introduced for the completeness of the presentation.

Solutions to Eqs. (3) and (4), which are singular at $r$ $=$ 0, can be written respectively as

$$\begin{aligned}&\psi _n^+ =K_{2n} \!\left( {k_y r} \right) \!\cos \! \left( {2n\theta } \right) , \quad n=0,1,2,\ldots ,\end{aligned}$$

(29)

$$\begin{aligned}&\psi _n^- =K_{2n-1} \!\left( {k_y r} \right) \!\sin \! \left( {\left( {2n-1} \right) \theta } \right) , \quad n=1,2,\ldots , \end{aligned}$$

(30)

where $K_{n}$ is the modified Bessel function of the second kind of order $n$. The preceding solutions can be represented as [15, Eqs. (B.101) and (B.103)]

$$\begin{aligned}&\psi _n^+ =\int _0^\infty {\cosh \! \left( {2n\mu } \right) \!\cos \! \left( {k_y x\sinh \left( \mu \right) } \right) \!{\text{ e }}^{-\nu \left( {z+h} \right) }} {\text{ d }}\mu , \quad z>-h,\end{aligned}$$

(31)

$$\begin{aligned}&\psi _n^- =\int _0^\infty {\sinh \! \left( {\left( {2n-1} \right) \mu } \right) \!\sin \! \left( {k_y x\sinh \left( \mu \right) } \right) \!{\text{ e }}^{-\nu \left( {z+h} \right) }} {\text{ d }}\mu , \quad z>-h, \end{aligned}$$

(32)

where $\nu =k_y \cosh \mu$.

The symmetric and antisymmetric multipoles, $\varphi _n^+$ and $\varphi _n^-$, may have the following forms:

$$\begin{aligned}&\varphi _n^+ =\psi _n^+ +\int _0^\infty {f^{+}\left( \mu \right) \!\cosh \! \left( {2n\mu } \right) \!\cos \! \left( {k_y x \sinh (\mu )} \right) }\!\cosh \! \left( {\nu \left( {z+h} \right) } \right) {\text{ d }}\mu ,\end{aligned}$$

(33)

$$\begin{aligned}&\varphi _n^- =\psi _n^- +\int _0^\infty {f^{-}\left( \mu \right) \!\sinh ({\left( {2n-1} \right) \mu })\!\sin \! \left( {k_y x\sinh \! \left( \mu \right) } \right) }\!\cosh ({\nu \left( {z+h} \right) }){\text{ d }}\mu . \end{aligned}$$

(34)

Obviously, Eqs. (33) and (34) satisfy the field equation in Eq. (3) and the water bottom condition in Eq. (4). The unknowns $f^{+}(\mu )$ and $f^{-}(\mu )$ can be determined using the free surface condition in Eq. (5). Then the symmetric and antisymmetric multipoles for the present problem can be written as

$$\begin{aligned}&\begin{aligned}&\varphi _n^+ =K_{2n} \!\left( {k_y r} \right) \!\cos ({2n\theta }) \\&\quad \qquad +\int _0^\infty {\frac{\left( {K+\nu } \right) {\text{ e }}^{-\nu h}\!\cosh \! \left( {2n\mu } \right) \!\cos \! \left( {k_y x\sinh \! \left( \mu \right) } \right) \!\cosh \! \left( {\nu \left( {z+h} \right) } \right) }{\nu \sinh \! \left( {\nu h} \right) -K\!\!\cosh \! \left( {\nu h} \right) }} {\text{ d }}\mu ,\quad n=0,1,2,\ldots , \\ \end{aligned} \end{aligned}$$

(35)

$$\begin{aligned}&\begin{aligned}&\varphi _n^- = K_{2n-1}\! \!\left( {k_y r} \right) \!\sin \! \left( {\left( {2n-1} \right) \theta } \right) \\&\quad \qquad +\int _0^\infty {\frac{\left( {K+\nu } \right) {\text{ e }}^{-\nu h}\!\sinh \! \left( {\left( {2n-1} \right) \mu } \right) \!\sin \left( {k_y x\sinh \! \left( \mu \right) } \right) \!\cosh \! \left( {\nu \left( {z+h} \right) } \right) }{\nu \sinh \! \left( {\nu h} \right) -K\!\!\cosh \! \left( {\nu h} \right) }} {\text{ d }}\mu ,\quad n=1,2,\ldots , \\ \end{aligned} \end{aligned}$$

(36)

where the path of the integration passes below the pole at $\mu =\kappa =\ln \left( {1/{\sin \beta }+\sqrt{1/{\sin ^{2}\beta }-1}} \right)$ to satisfy the radiation conditions in Eq. (6) [34, 35].

As $x\rightarrow \pm \infty$, we have

$$\begin{aligned}&\varphi _n^+ \sim \frac{\text{ i }\pi \!\cosh \! \left( {2n\kappa } \right) }{2k_x hN_0^2 }\cosh \! \left( {k\left( {z+h} \right) } \right) {\text{ e }}^{\pm \mathrm{{i}}k_x x},\end{aligned}$$

(37)

$$\begin{aligned}&\varphi _n^- \sim \pm \frac{\pi \!\sinh \! \left( {\left( {2n-1} \right) \kappa } \right) }{2k_x hN_0^2 }\cosh \! \left( {k\left( {z+h} \right) } \right) {\text{ e }}^{\pm \mathrm{{i}}k_x x}, \end{aligned}$$

(38)

where $N_0^2 =\left[ {1+{\sinh \! \left( {2kh} \right) }/{\left( {2kh} \right) }} \right] /2$.

The multipoles can be written as power series expansions [29, Eq. A.4]:

$$\begin{aligned}&\varphi _n^+ =K_{2n} \!\left( {k_y r} \right) \!\cos \! \left( {2n\theta } \right) +\sum _{m=0}^\infty {A_{mn}^+ I_{2m} \!\left( {k_y r} \right) \!\cos \! \left( {2m\theta } \right) } , \quad n=0,1,2,\ldots ,\end{aligned}$$

(39)

$$\begin{aligned}&\varphi _n^- =K_{2n-1} \!\left( {k_y r} \right) \!\sin \! \left( {\left( {2n-1} \right) \theta } \right) +\sum _{m=1}^\infty {A_{mn}^- I_{2m-1}\! \left( {k_y r} \right) \!\sin \! \left( {\left( {2m-1} \right) \theta } \right) } , \quad n=1,2,\ldots , \end{aligned}$$

(40)

where $I_{m}$ is the modified Bessel function of the first kind of order $m$ and

$$\begin{aligned}&A_{mn}^+ =\varepsilon _m \int _0^\infty {\frac{\left( {K+\nu } \right) {\text{ e }}^{-\nu h}\cosh \! \left( {2n\mu } \right) \!\cosh \! \left( {2m\mu } \right) }{\nu \!\sinh \! \left( {\nu h} \right) -K\!\!\cosh \! \left( {\nu h} \right) }} {\text{ d }}\mu ,\end{aligned}$$

(41)

$$\begin{aligned}&A_{mn}^- =2\int _0^\infty {\frac{\left( {K+\nu } \right) {\text{ e }}^{-\nu h}\!\sinh \! \left( {\left( {2n-1} \right) \mu } \right) \!\sinh \! \left( {\left( {2m-1} \right) \mu } \right) }{\nu \sinh \! \left( {\nu h} \right) -K\!\!\cosh \! \left( {\nu h} \right) }} {\text{ d }}\mu , \end{aligned}$$

(42)

in which the path of the integration passes below the pole at $\mu =\kappa$, and $\varepsilon _0 =1$ and $\varepsilon _m =2$ ($m\ge 1)$.

Computational methods for such types of integrals in Eqs. (41) and (42) can be found in Linton [36, Eqs. (3.7) and (4.11)]. For example, the integral in Eq. (41) can be rewritten as

$$\begin{aligned} \begin{aligned} A_{mn}^+&= 2\varepsilon _m \text{ PV }\int _0^b {\frac{S\left( {\nu ,\mu } \right) -\frac{k_y \sinh \left( \mu \right) \left[ {\tanh \left( {\nu h} \right) +{\nu h}/{\cosh ^{2}\left( {\nu h} \right) }} \right] }{k_x \left[ {\tanh \left( {kh} \right) +{kh}/{\cosh ^{2}\left( {kh} \right) }} \right] }S({k,\kappa })}{\nu \tanh \! \left( {\nu h} \right) -K}} {\text{ d }}\mu \\&\quad + 2\varepsilon _m \int _b^{+\infty } {\frac{(K+\nu )\!\cosh \! \left( {2n\mu } \right) \!\cosh \! \left( {2m\mu } \right) }{\left[ {\nu \tanh \! \left( {\nu h} \right) -K} \right] \left( {{\text{ e }}^{2\nu h}+1} \right) }} {\text{ d }}\mu + \varepsilon _m \frac{\text{ i }\pi \!\text{ cosh }\!\left( {\text{2 }m\kappa } \right) \!\text{ cosh }\!\left( {\text{2 }n\kappa } \right) }{2k_x hN_0^2 }, \end{aligned} \end{aligned}$$

(43)

where PV denotes the principal value integral; the function $S\left( {x,y} \right)$ is defined as $S\left( {x,y} \right) =(K+x)\cosh \! \left( {2ny} \right) \cosh \left( {2my} \right) /{\left( {{\text{ e }}^{2xh}+1} \right) }$; the symbol $b$ denotes the positive real root of the relationship

$$\begin{aligned} \left[ {k_y \cosh \! \left( b \right) } \right] \tanh \! \left( {k_y h\!\cosh \left( b \right) } \right) =2K-k_y \tanh \! \left( {k_y h} \right) \end{aligned}$$

(44)

using the following integral:

$$\begin{aligned} \begin{aligned} \text{ PV }\int _0^{2\left[ {K-k_y \tanh \left( {k_y h} \right) } \right] } {\frac{{\text{ d }}\tilde{\nu }}{\tilde{\nu }-\left[ {K-k_y \tanh \! \left( {k_y h} \right) } \right] }}&=\text{ PV }\int _0^b {\frac{k_y \sinh \! \left( \mu \right) \!\left[ {\tanh \! \left( {\nu h} \right) +{\nu h}/{\cosh ^{2}\!\left( {\nu h} \right) }} \right] }{\nu \;\tanh \! \left( {\nu h} \right) -K}} {\text{ d }}\mu = 0, \end{aligned} \end{aligned}$$

(45)

in which $\tilde{\nu }=\nu \;\tanh \! \left( {\nu h} \right) -k_y \tanh \! \left( {k_y h} \right)$. A similar expression can be obtained for Eq. (42).