Skip to main content
SpringerLink
Log in

Flutter of a viscoelastic strip

  • Published:
Journal of Engineering Mathematics Aims and scope Submit manuscript

Abstract

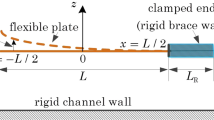
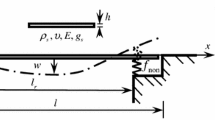
An approximate solution of the problem of flutter of a cantilever clamped viscoelastic strip is obtained under conditions where the flow velocity vector is parallel to the plane of the strip and forms an angle with its edges, which can take arbitrary values. The approximate solution in all the cases is based on the linear combinations of polynomials, which satisfy the boundary conditions. Approximate estimates of the values of the critical flutter speed are obtained by using the Laplace transform in time and a Galerkin expansion for the spatial structures. The nature of the changes in the critical speed with respect to the value of the angle of flow is examined. It is shown that for any non-negative angle of flow with increasing velocity of flow there is an instability in the form of flutter. For negative angles of the flow, either flutter or a cylindrical bending of the strip is observed. Principally, a new mechanical effect is found: there is a whole sector of directions for which increase in flow rate leads to a cylindrical bending.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Il’yushin AA (1994) Dynamics. Mech Bull Transl Vestnik of Moscow State Univ Mech 49(3): 19–26

    Google Scholar 

  2. Movchan AA (1955) Some questions in plate vibrations, moving in a gas. In: Proceedings of the Institute of Mechanics. USSR Academy of Sciences, Moscow, p 36 (in Russian)

  3. Movchan AA (1956) About the oscillations of the plate, moving in a gas. J Appl Math Mech 20:221–222 (in Russian)

    Google Scholar 

  4. Novichkov IuN (1978) Flutter of plates and shells. In: Results in science and technics. Mech. of deformable solids, vol 11. VINITI Publ., Moscow, pp 67–122 (in Russian)

  5. Algazin SD, Kiiko IA (2006) Flutter of plates and shells. Nauka, Moscow (in Russian)

    Google Scholar 

  6. Il’yushin AA, Kiiko IA (1994) A new formulation of the problem of the flutter of a hollow shell. J Appl Math Mech 58(3): 545–549

    Article  MathSciNet  MATH  Google Scholar 

  7. Kiiko IA (1999) Formulation of the problem of the flutter of a shell of revolution and a shallow shell in a high-velocity supersonic gas flow. J Appl Math Mech 63(2): 305–312

    Article  MathSciNet  Google Scholar 

  8. Kiiko IA, Kudryavtsev BIu (1999) Nonlinear aeroelastic oscillations of rectangular plates. Bulletin of Moscow State University. Ser. 1. Math. Mech. Num. 1, pp 68–71 (in Russian)

  9. Kudryavtsev BIu (2006) Investigation of the flutter of a nonlinear formulation, vol 1. Izvestiya of the Tula State University, pp 61–68 (in Russian)

  10. Isaulova TN, Lavit IM (2009) Aerodynamic stability of a cantilever clamped oblique plate, vol 2. Izvestiya of the Tula State University, pp 90–104 (in Russian)

  11. Larionov GS (1970) Stability of vibrations of viscoelastic plate at hypersonic speeds. Issues Comput Appl Math 3:156–163 (in Russian)

    Google Scholar 

  12. Matyash VI (1971) Flutter of a viscoelastic plate. Mech Polym 6:1077–1083 (in Russian)

    Google Scholar 

  13. Larionov GS (1974) Nonlinear flutter of viscoelastic plates. Russ Mech Solids (Izvestiya USSR Academy of Sciences—Mech of Solids) 4:95–100 (in Russian)

  14. Il’yushin AA, Larionov GS, Filatov AN (1969) About averaging in systems of nonlinear integro-differential equations. Rep USSR Acad Sci 188(1):49–52 (in Russian)

    Google Scholar 

  15. Kiiko IA (1996) Flutter of a viscoelastic plate. J Appl Math Mech 60(1): 167–170

    Article  Google Scholar 

  16. Pokazeyev VV (2008) Flutter of a cantilevered elastic and viscoelastic strip. J Appl Math Mech 72(4): 446–451

    Article  MathSciNet  Google Scholar 

  17. Kiiko IA, Pokazeev VV (2005) Vibrations and stability of a viscoelastic strip placed into gas flow. Dokl Phys 50(3): 158–160

    Article  ADS  Google Scholar 

  18. Ditkin VV, Proudnikov AP (1975) Operational calculus. High School, Moscow (in Russian)

    Google Scholar 

  19. Bolotin VV (1961) Nonconservative problem in the theory of elastic stability. Fizmatgiz, Moscow (in Russian)

    Google Scholar 

  20. Kudryavtsev BIu (1995) Vibrations and stability of an elastic strip in a supersonic flow of gas. Dissertation, Moscow State University MAMI, p 96 (in Russian)

  21. Aleksandrov VM, Grishin SA (1994) Dynamics of a conical shell containing supersonic gas flow. J Appl Math Mech 58(4): 703–712

    Article  MathSciNet  MATH  Google Scholar 

  22. Pokazeyev VV (2006) Flutter of viscoelastic orthotropic strip, vol 12. Izvestiya of the Tula State University, pp 158–164 (in Russian)

Download references

Author information

Authors and Affiliations

  1. Mechanical and Mathematical Faculty of Moscow State University, Vorob’evy Gory, Moscow, Russia, 119991

    I. A. Kiiko

  2. Moscow State Technical University “MAMI”, 38 Bol’shaya Semenovskaya Street, Moscow, Russia, 105839

    V. V. Pokazeyev

Authors
  1. I. A. Kiiko
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. V. V. Pokazeyev
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to V. V. Pokazeyev.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Kiiko, I.A., Pokazeyev, V.V. Flutter of a viscoelastic strip. J Eng Math 78, 213–222 (2013). https://doi.org/10.1007/s10665-012-9534-4

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10665-012-9534-4

Keywords

Search

Navigation