Kinematic instabilities in two-layer eccentric annular flows, part 2: shear-thinning and yield-stress effects

Abstract

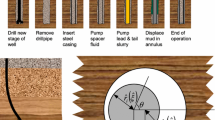
This paper investigates the possibility of kinematic interfacial instabilities occurring during the industrial process of primary cementing of oil and gas wells. This process involves flows in narrow eccentric annuli that are modelled via a Hele-Shaw approach. The fluids present in primary cementing are strongly non-Newtonian, usually exhibiting shear-thinning behaviour and often with a yield stress. The study is a sequel to Moyers-González and Frigaard (J Eng Math, DOI 10.1007/s10665-007-9178-y, 2007), in which the base analysis has been developed for the case of two Newtonian fluids. The occurrence of static mud channels in primary cementing has been known of since the 1960s, (see McLean et al. 1966; SPE 1488), and is a major cause of process failure. This phenomenon is quantified, which provides a simple semi-analytic expression for the maximal volume of residual fluid left behind in the annulus, f _static, and illustrate the dependency of f _static on its five dimensionless parameters. It is shown that three of the four different types of static channel flows are linearly stable. Via dimensional analysis, it is shown that the base flows depend on a minimal set of eight dimensionless parameters and the stability problem depends on an additional two dimensionless parameters. This large dimensional parameter space precludes use of the full numerical solution to the stability problem as a predictive tool or for studying the various stability regimes. Instead a semi-analytical approach has been developed based on solution of the long-wavelength limit. This prediction of instability can be evaluated via simple quadrature from the base flow and is suitable for use in process optimisation.