Skip to main content
SpringerLink
Log in

Transformation of flexural gravity waves by heterogeneous boundaries

  • Published:
Journal of Engineering Mathematics Aims and scope Submit manuscript

Abstract

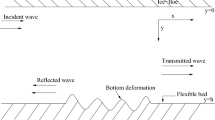
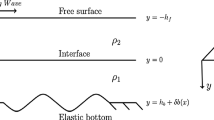
The transformation of flexural gravity waves due to wave scattering by heterogeneous boundaries is investigated under the assumption of the linearized water-wave theory. The heterogeneous boundaries include step-type bottom topography as well as heterogeneity in the material property of a floating ice-sheet. By applying the generalized expansion formulae along with the corresponding orthogonal mode-coupling relations, the boundary-value problem (BVP) is reduced to linear system of algebraic equations. The system of equations is solved numerically to determine the full solution of the problem under consideration. Energy relations are derived and used to check the accuracy of the computational results of the scattering problem. Explicit relations for the shoaling and scattering coefficients due to the change in water depth and heterogeneous ice-sheet are derived. These derivations are based on the law of conservation of energy flux under the assumptions of the linearized shallow-water theory. The change in water depth and the structural characteristics of the medium significantly contribute to the change in the scattering and shoaling coefficients and the deflection of the structure. The present results are likely to play a significant role in the analysis of flexural gravity-wave propagation in problems of variable topography for which a direct computational approach is being utilized.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Greenhill AG (1887). Wave motion in hydrodyanamics. Am J Math 9: 62–112

    Article  Google Scholar 

  2. Williams TD and Squire VA (2004). Oblique scattering of plane flexural-gravity waves by heterogeneities in sea-ice. Proc R Soc Lond A 460(2052): 3469–3497

    MATH  ADS  MathSciNet  Google Scholar 

  3. Fox C and Squire VA (1994). On the oblique reflection and transmission of ocean waves at shore fast sea ice. Phil Trans R Soc Lond A 347: 185–218

    Article  MATH  ADS  Google Scholar 

  4. Sahoo T, Yip TL and Chwang AT (2001). Scattering of surface waves by a semi-infinite floating elastic plate. Phys Fluid 13(11): 3215–3222

    Article  ADS  Google Scholar 

  5. Evans DV and Porter R (2003). Wave scattering by narrow cracks in ice sheets floating on water of finite depth. J Fluid Mech 484: 143–165

    Article  MATH  ADS  MathSciNet  Google Scholar 

  6. Manam SR, Bhattacharjee J and Sahoo T (2006). Expansion formulae in wave structure interaction problems. Proc R Soc Lond A 462(2065): 263–287

    Article  MATH  ADS  MathSciNet  Google Scholar 

  7. Watanabe E, Utsunomiya T and Wang CM (2004). Hydroelastic analysis of pontoon-type VLFS: a literature survey. Eng Struct 26: 245–256

    Article  Google Scholar 

  8. Chen X, Wu Y, Cui W and Jensen JJ (2006). Review of hydroelasticity theories for global response of marine structures. Ocean Eng 33: 439–457

    Article  Google Scholar 

  9. Newman JN (1965). Propagation of water waves over an infinite step. J Fluid Mech 23(Part 2): 399–415

    Article  ADS  MathSciNet  Google Scholar 

  10. Dingemans MW (1997) Water wave propagation over uneven bottoms, Part-I—Linear wave propagation. Advanced series on Ocean Engineering—vol 13, World Scientific

  11. Berkhoff JCW (1972) Computation of combined refraction-diffraction. Proceedings of 13th International conference on Coastal Engineering. ASCE 1, pp 472–490

  12. Rhee JP (1997). On the transmission of water waves over a shelf. Appl Ocean Res 19: 161–169

    Article  Google Scholar 

  13. Rhee JP (2001). A note on the diffraction of obliquely incident water waves by a stepwise obstacle. Appl Ocean Res 23: 299–304

    Article  MathSciNet  Google Scholar 

  14. Ehrenmark UT (1998). Oblique Wave incidence on a plane beach: the classical problem revisited. J Fluid Mech 368: 291–319

    Article  MATH  ADS  MathSciNet  Google Scholar 

  15. Sturova IV (2001). The diffraction of surface waves by an elastic platform floating on shallow water. J Appl Math Mech 65(1): 109–117

    Article  Google Scholar 

  16. Wang CD and Meylan MH (2002). The linear wave response of a floating thin plate on water of variable depth. Appl Ocean Res 24: 163–174

    Article  Google Scholar 

  17. Andrianov AD, Hermans AJ (2002) Diffraction of surface waves by VLFP on water of infinite, finite or shallow depth. DAY on Diffraction, Proceedings, International seminar 5–8 June, pp 13–23

  18. Williams TD and Squire VA (2006). Scattering of flexural-gravity waves at the boundaries between three floating sheets with applications. J Fluid Mech 569: 113–140

    Article  MATH  ADS  MathSciNet  Google Scholar 

  19. Porter D and Porter R (2004). Approximations to wave scattering by an ice sheet of variable thickness over undulating bed topography. J Fluid Mech 509: 145–179

    Article  MATH  ADS  MathSciNet  Google Scholar 

  20. Belibassakis KA and Athanassoulis GA (2006). A coupled-mode technique for weakly nonlinear wave interaction with large floating structures lying over variable bathymetry regions. Appl Ocean Res 28: 59–76

    Article  Google Scholar 

  21. Lawrie JB and Abrahams ID (1999). An orthogonality relation for a class of problems with high-order boundary conditions; Applications in sound-structure interaction. Q J Mech Appl Math 52(2): 161–181

    Article  MATH  MathSciNet  Google Scholar 

  22. Magrab EB (1979). Vibrations of elastic structural members, SIJTHOFF and NOORDHOFF. Alphen aan den Rijn, The Netherlands

    Google Scholar 

  23. Wehausen JV, Laitone EV (1960) Surface waves. Encyclopedia of Physics, vol 9, Springer, Berlin, 9, pp 446–814. also at http://www.coe.berkeley.edu/Surface Waves (Accessed 1 Aug 2002)

  24. Dean RG, Dalrymple RA (2001) Water wave mechanics for engineers and scientists. Allied Publishers Limited, World Scientific

  25. Karmakar D, Bhattacharjee J and Sahoo T (2007). Expansion formulae for wave structure interaction problems with applications in hydroelasticity. Intl J Eng Sci 45: 807–828

    Article  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Ocean Engineering and Naval Architecture, Indian Institute of Technology, Kharagpur, 721 302, India

    Joydip Bhattacharjee, Debabrata Karmakar & Trilochan Sahoo

Authors
  1. Joydip Bhattacharjee
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Debabrata Karmakar
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Trilochan Sahoo
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Trilochan Sahoo.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Bhattacharjee, J., Karmakar, D. & Sahoo, T. Transformation of flexural gravity waves by heterogeneous boundaries. J Eng Math 62, 173–188 (2008). https://doi.org/10.1007/s10665-007-9203-1

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10665-007-9203-1

keywords

Search

Navigation