Skip to main content
SpringerLink
Log in

A diagonal-mass-matrix triangular-spectral-element method based on cubature points

  • Original Paper
  • Published:
Journal of Engineering Mathematics Aims and scope Submit manuscript

Abstract

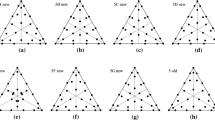
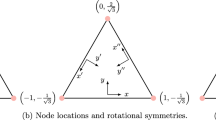
The cornerstone of nodal spectral-element methods is the co-location of the interpolation and integration points, yielding a diagonal mass matrix that is efficient for time-integration. On quadrilateral elements, Legendre–Gauss–Lobatto points are both good interpolation and integration points; on triangles, analogous points have not yet been found. In this paper, a promising set of points for the triangle that were only available for polynomial degree N ≤ 5 are used. However, the derivation of these points is generalized to obtain degree N ≤ 7 points, which are referred to as cubature points because their selection is based on their integration accuracy. The diagonal-mass-matrix (DMM) triangular-spectral-element (TSE) method based on these points can be used for any set of equations and any type of domain. Because these cubature points integrate up to order 2N along the element boundaries and yield a diagonal mass matrix, they allow the triangular spectral elements to compete with quadrilateral spectral elements in terms of both accuracy and efficiency, while offering more geometric flexibility in the choice of grids. It is shown how to implement this DMM TSE for a variety of applications involving elliptic and hyperbolic equations on different domains. The DMM TSE method yields comparable accuracy to the exact integration (non-DMM) TSE method, while being far more efficient for time-dependent problems.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Patera AT (1984) A spectral element method for fluid dynamics—laminar flow in a channel expansion. J Comp Phys 54:468–488

    Article  MATH  ADS  Google Scholar 

  2. Solin P, Segeth K, Dolezel I (2003) Higher-order finite element methods. Chapman and Hall/CRC Press

  3. Sherwin SJ, Karniadakis GE (1995) A triangular spectral element method; applications to the incompressible Navier-Stokes equations. Comp Meth Appl Mech Eng 123:189–229

    Article  MATH  MathSciNet  Google Scholar 

  4. Hesthaven JS (1998) From electrostatics to almost optimal nodal sets for polynomial interpolation in a simplex. SIAM J Num Anal 35:655–676

    Article  MATH  MathSciNet  Google Scholar 

  5. Taylor MA, Wingate BA, Vincent RE (2000) An algorithm for computing Fekete points in the triangle. SIAM J Num Anal 38:1707–1720

    Article  MATH  MathSciNet  Google Scholar 

  6. Warburton T, Pavarino LF, Hesthaven JS (2000) A pseudo-spectral scheme for the incompressible Navier–Stokes equations using unstructured nodal elements. J Comp Phys 164:1–21

    Article  MATH  ADS  MathSciNet  Google Scholar 

  7. Giraldo FX, Warburton T (2005) A nodal triangle-based spectral element method for the shallow water equations on the sphere. J Comp Phys 207:129–150

    Article  MATH  ADS  MathSciNet  Google Scholar 

  8. Cohen G, Joly P, Roberts JE, Tordjman N (2001) Higher order triangular finite elements with mass lumping for the wave equation. SIAM J Num Anal 38:2047–2078

    Article  MATH  MathSciNet  Google Scholar 

  9. Taylor MA, Wingate BA (2000) A generalized diagonal mass matrix spectral element method for non-quadrilateral elements. Appl Num Math 33:259–265

    Article  MATH  MathSciNet  Google Scholar 

  10. Helenbrook B (2004) Polynomial bases suitable for mass lumping on triangles. Int Conf Spectral and High-Order Methods (ICOSAHOM).

  11. Cohen G, Joly P, Tordjman N (1995). Higher order triangular finite elements with mass lumping for the wave equation. In: Cohen G, Becahe E, Joly P, Roberts JE (eds). Proc. 3rd Int. Conf. on Mathematical and Numerical Aspects of Wave Propagation. SIAM, Philadelphia

    Google Scholar 

  12. Mulder WA (2001) Higher-order mass-lumped finite elements for the wave equation. J Comp Acoust 9:671–680

    Article  MathSciNet  Google Scholar 

  13. Komatitsch D, Martin R, Tromp J, Taylor MA, Wingate BA (2001) Wave propagation in 2-D elastic media using a spectral element method with triangles and quadrangles. J. Comp. Acoustics 9:703–718

    Article  Google Scholar 

  14. Cools R, Rabinowitz P (1993) Monomial cubature rules since Stroud: a compilation. J Comp and Appl Math 48:309–326

    Article  MATH  MathSciNet  Google Scholar 

  15. Lyness J, Cools R (1994) A survey of numerical cubature over triangles. Appl Math 48:127–150

    ADS  MathSciNet  Google Scholar 

  16. Cools R (1997) Constructing cubature formulae: the science behind the art. Acta Numerica 6:1–54

    Article  MathSciNet  Google Scholar 

  17. Cools R (1999) Monomial cubature rules since Stroud: a compilation—part 2. J Comp Appl Math 112:21–27

    Article  MATH  MathSciNet  Google Scholar 

  18. Cools R (2003) An encyclopaedia of cubature formulas. J Complexity 19:445–453. Online database located at http://www.cs.kuleuven.ac.be/~nines/research/ecf/ecf.html

    Google Scholar 

  19. Lyness J, Jespersen D (1975) Moderate degree symmetric quadrature rules for the triangle. J Inst Math Appl 15:19–32

    Article  MATH  MathSciNet  Google Scholar 

  20. Wandzura S, Xiao H (2003) Symmetric quadrature rules on a triangle. Comp Math Appl 45:1829–1840

    Article  MATH  MathSciNet  Google Scholar 

  21. Taylor MA, Wingate BA, Bos LP (2006) A cardinal function algorithm for computing multivariate quadrature points. SIAM J Num Anal (to appear)

  22. Proriol J (1957) Sur une famille de polynomes á deux variables orthogonaux dans un triangle. C R Acad Sci Paris 257:2459

    MathSciNet  Google Scholar 

  23. Dubiner M (1991) Spectral methods on triangles and other domains. J Scientific Comp 6:345–390

    Article  MATH  MathSciNet  Google Scholar 

  24. Karniadakis GE, Sherwin SJ (1999) Spectral/hp element methods for CFD, Oxford Univ Press

  25. Taylor M, Tribbia J, Iskandarani M (1997) The spectral element method for the shallow water equations on the sphere. J Comp Phys 130:92–108

    Article  MATH  ADS  Google Scholar 

  26. Boyd J (1996). The erfc-log filter and the asymptotics of the Euler and Vandeven sequence accelerations. In: Ilin AV, Scottv LR (eds). Proceedings of the Third International Conference on Spectral and High Order Methods. Houston Journal of Mathematics, Houston Texas, 267–276

    Google Scholar 

  27. Maday Y, Patera AT (1987). Spectral element methods for the incompressible Navier Stokes equations. In: Noor AK, Oden JT, (eds). state of the art surveys on computational mechanics. ASME, New York, 71–143

    Google Scholar 

  28. Williamson DL, Drake JB, Hack JJ, Jakob R, Swarztrauber PN (1992) A standard test set for numerical approximations to the shallow water equations in spherical geometry. J Comp Phys 102:211–224

    Article  MATH  ADS  MathSciNet  Google Scholar 

  29. Karniadakis GE, Israeli M, Orszag SA (1991) High-order splitting methods for the incompressible Navier-Stokes equations. J Comp Phys 97:414–443

    Article  MATH  ADS  MathSciNet  Google Scholar 

  30. Giraldo FX (2005) Semi-implicit time-integrators for a scalable spectral element atmospheric model. Quart J Roy Meteorol Soci 131:2431–2454

    Article  ADS  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Naval Postgraduate School, Monterey, CA, 93943, USA

    F. X. Giraldo

  2. Sandia National Laboratory, Albuquerque, NM, 87185, USA

    M. A. Taylor

Authors
  1. F. X. Giraldo
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. M. A. Taylor
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to F. X. Giraldo.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Giraldo, F.X., Taylor, M.A. A diagonal-mass-matrix triangular-spectral-element method based on cubature points. J Eng Math 56, 307–322 (2006). https://doi.org/10.1007/s10665-006-9085-7

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10665-006-9085-7

Keywords

Search

Navigation