Abstract
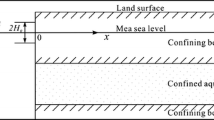
Tidal watertable fluctuations in a coastal aquifer are driven by tides on a moving boundary that varies with the beach slope. Based on a linearised one-dimensional Boussinesq model, tidal signals in the aquifer are analysed, focusing on the watertable overheight induced by the moving-boundary condition. The watertable overheight is an important parameter related to the estimation of submarine groundwater discharge (SGD). This note presents a new analytical approach to solving the Boussinesq equation with the Fourier-series expansion. Moreover, it is proved that the asymptote of watertable overheight normalised by the tidal amplitude is unit as a controlling parameter (( \(\varepsilon_0\))), combining the aquifer properties and tidal frequency, approaches infinity. Physically, this condition represents beaches of very low drainage capacity.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Philip JR (1973) Periodic nonlinear diffusion: an integral relation and its physical consequences. Aust J Phys 26:513–519
Parlange JY, Stagnitti F, Starr JL, Braddock RD (1984) Free-surface flow in porous media and periodic solution of the shallow-flow approximation. J Hydrol 70:251–263
Nielsen P (1990) Tidal dynamics of the water table in beaches. Water Resour Res 26:2127–2134
Li L, Barry DA, Stagnitti F, Parlange JY, Jeng DS (2000) Beach water table fluctuations due to spring-neap tides: moving boundary effects. Adv Water Resour 23:817–824
Simmons GM (1992) Importance of submarine groundwater discharge and sea water cycling to material flux across sediment/water interfaces in marine environments. Mar Ecol Prog Ser 84:173–184
Church TM (1996) A groundwater route for the water cycle. Nature 380:579–580
Moore WS (1996) Large groundwater inputs to coastal waters revealed by 226Ra enrichment. Nature 380: 612–614
Li L, Barry DA, Stagnitti F, Parlange JY (1999) Submarine groundwater discharge and associated chemical input to a coastal sea. Water Resour Res 35:3253–3259
Li HL, Jiao JJ (2003) Tide-induced seawater-groundwater circulation in a multi-layer coastal leaky aquifer system. J Hydrol 274:211–224
Callaghan D, Nielsen P (accepted) A note on the theoretical rise in mean groundwater elevation for very flat beaches driven solely by the tide. Adv Water Resour
Bear J (1972) Dynamics of fluids in porous media. Amsterdam Elsevier, New York
Harris JW, Stocker H (1998) Handbook of mathematics and computational science. Springer-Verlag, New York
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Song, Z., Li, L., Nielsen, P. et al. Quantification of tidal watertable overheight in a coastal unconfined aquifer. J Eng Math 56, 437–444 (2006). https://doi.org/10.1007/s10665-006-9052-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10665-006-9052-3