Flows of inelastic non-Newtonian fluids through arrays of aligned cylinders. Part 2. Inertial effects for square arrays

Abstract

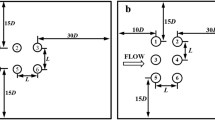
Numerical simulations are presented for flows of inelastic non-Newtonian fluids through periodic arrays of aligned cylinders. The truncated power-law fluid model is used for the relationship between the viscous stress and the rate-of-strain tensor. Results for the drag coefficient for creeping flows of such fluids have been presented in a companion paper [1]. In this second part the effects of finite fluid inertia are investigated for flows through square arrays. It is shown that the Reynolds-number dependence of the drag coefficient of a cylinder in the array is of the form C _d≡ F/(ηU) = k ₀ + k ₂ Re²+ .. for small values of the Reynolds number Re ≡ ρaU/η, where F is the drag force, U is the averaged velocity in the array, η = K (U/a)^n-1 is a viscosity scale with K and n the power-law coefficient and index and a the cylinder radius, and k ₀ is the drag coefficient for creeping flows. The proportionality constant k ₂ depends on the way the drag coefficient and the Reynolds number are defined. It is shown that the observed strong dependence of k ₂ on n can almost be eliminated by using length scales different from a in the viscosity scales η used in the definition of Re and in the definition of the drag coefficient. Numerical simulation results are also presented for the velocity variance components. Results for flows at moderate Reynolds number, of order 100, are also presented; these are qualitatively similar to those for Newtonian fluids. The value of the Reynolds number beyond which the flow becomes unsteady was related to the Newtonian fluid case by rescaling. These results for moderate-Reynolds-number flow are compared against previously published experimental data.