International trade, technological change and wage inequality in the UK economy

Abstract

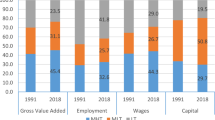
This paper examines the joint impact of international trade and technological change on UK wages across different skill groups. International trade is measured as changes in product prices and technological change as total factor productivity (TFP) growth. We take account of a multi-sector and multi-factor of production economy and use mandated wage methodology in order to create an well-balanced approach in terms of theoretical and empirical cohesion. We use data from the EU KLEMS database and analyse the impact of both product price changes and TFP changes of 11 UK manufacturing sectors on factor rewards of high-, medium- and low-skilled workers. Results show that real wages of skill groups are significantly driven by the sector bias of price change and TFP growth of several sectors of production. Furthermore, we estimate the share of the three different skill groups on added value for each year from 1970 to 2005. The shares indicate structural change in the UK economy. Results show a structural change owing to decreasing shares of low-skilled workers and increasing shares of medium-skilled and high-skilled workers over the years.

Appendix

1.1 Cost functions of a two sector and two factor economy

Based on Eq. (5) the factor price ratio of sector 1 reveals as

$$ \frac{w_{1}}{w_{2}}=\frac{\alpha_{11}}{\alpha _{12}}\frac{V_{12}}{V_{11}} $$

(33)

and based on Eq. (6) the factor price ratio of sector 2 reveals as

$$ \frac{w_{1}}{w_{2}}=\frac{\alpha_{21}}{\alpha _{22}}\frac{V_{22}}{V_{21}}. $$

(34)

Hence, factor intensity of sector 1 is given by

$$ \frac{V_{12}}{V_{11}}=\frac{w_{1}}{w_{2}}\frac{\alpha_{12}}{\alpha _{11}} $$

(35)

and of sector 2 by

$$ \frac{V_{22}}{V_{21}}=\frac{w_{1}}{w_{2}}\frac{\alpha_{22}}{\alpha _{21}}. $$

(36)

Reinserting factor intensity (35) into (5) yields

$$ \begin{aligned} w_{1} &=p_{1}A_{1}\alpha_{11}\left( \frac{w_{1}}{w_{2}}\frac{\alpha_{12}}{\alpha_{11}}\right)^{\alpha_{12}}\\ w_{2} &=p_{1}A_{1}\alpha_{12}\left( \frac{w_{2}}{w_{1}}\frac{\alpha_{11}}{\alpha_{12}}\right)^{\alpha_{11}}. \end{aligned} $$

(37)

Hence, by rearranging, the cost function of sector 1 reveals as

$$ p_{1}=\frac{1}{A_{1}}\frac{w_{1}^{(1-\alpha_{12})}w_{2}^{\alpha _{12}}}{\alpha_{12}^{\alpha_{12}}(1-\alpha_{12})^{(1-\alpha _{12})}}. $$

(38)

Reinserting factor intensity (36) into (6) yields

$$ \begin{aligned} w_{1} &=p_{2}A_{2}\alpha_{21}\left( \frac{w_{1}}{w_{2}}\frac{\alpha_{22}}{\alpha_{21}}\right)^{\alpha_{22}} \\ w_{2} &=p_{2}A_{2}\alpha_{22}\left( \frac{w_{2}}{w_{1}}\frac{\alpha_{21}}{\alpha_{22}}\right)^{\alpha_{21}} \end{aligned} $$

(39)

Hence, by rearranging, the cost function of sector 2 reveals as

$$ p_{2}=\frac{1}{A_{2}}\frac{w_{2}^{(1-\alpha_{21})}w_{1}^{\alpha _{21}}}{\alpha_{21}^{\alpha_{21}}(1-\alpha_{21})^{(1-\alpha _{21})}}. $$

(40)

1.2 Determination of factor prices of a two sector and two factor economy

The equation system (8) reveals in matrix notation as

$$ \left( \begin{array}{ll} \alpha_{11} & \alpha_{12} \\ \alpha_{21} & \alpha_{22} \end{array} \right) \left( \begin{array}{l} \ln w_{1} \\ \ln w_{2} \end{array} \right)=\left( \begin{array}{l} \ln \overline{p_{1}} \\ \ln \overline{p_{2}} \end{array} \right). $$

(41)

Solving by Cramer’s Rule yields

$$ \begin{aligned} \ln w_{1}=\frac{Det(\underline{\Upphi_{1}})}{Det(\underline{\Upphi })}&=\frac{\ln \overline{p_{1}}\cdot \alpha_{22}-\ln \overline{p_{2}}\cdot \alpha_{12}}{\alpha_{11}\cdot \alpha_{22}-\alpha_{21}\cdot \alpha_{12}}=\frac{\ln\overline{p_{1}}\cdot \Upphi_{11}+\ln \overline{p_{2}}\cdot \Upphi_{21}}{\alpha_{11}\cdot \alpha_{22}-\alpha_{21}\cdot \alpha_{12}} \\ \ln w_{2}=\frac{Det(\underline{\Upphi_{2}})}{Det(\underline{\Upphi })}&=\frac{\ln \overline{p_{2}}\cdot \alpha_{11}-\ln \overline{p_{1}}\cdot \alpha_{21}}{\alpha_{11}\cdot \alpha_{22}-\alpha_{21}\cdot \alpha_{12}}=\frac{\ln\overline{p_{2}}\cdot \Upphi_{22}+\ln \overline{p_{1}}\cdot \Upphi_{12}}{\alpha_{11}\cdot \alpha_{22}-\alpha_{21}\cdot \alpha_{12}} \end{aligned} $$

(42)

$$ \begin{aligned} Det(\underline{\Upphi })\cdot \ln w_{1} &=\sum\limits_{i=1}^{2}\Upphi_{i1}\cdot \ln \overline{p_{i}} \\ Det(\underline{\Upphi })\cdot \ln w_{2} &=\sum\limits_{i=1}^{2}\Upphi_{i2}\cdot \ln \overline{p_{i}}, \end{aligned} $$

(43)

whereby determinants are given by

$$ \begin{aligned} Det\left( \begin{array}{ll} \alpha_{11} & \alpha_{12} \\ \alpha_{21} & \alpha_{22} \end{array} \right) &=Det(\underline{\Upphi })=\Upphi \\ Det\left( \begin{array}{ll} \ln \overline{p_{1}} & \alpha_{12} \\ \ln \overline{p_{2}} & \alpha_{22} \end{array} \right) &=Det(\underline{\Upphi_{1}}) \\ Det\left( \begin{array}{ll} \alpha_{11} & \ln \overline{p_{1}} \\ \alpha_{21} & \ln \overline{p_{2}} \end{array} \right) &=Det(\underline{\Upphi_{2}}), \end{aligned} $$

(44)

with adjoints $\Upphi_{11}=\alpha_{22}, \Upphi_{21}=-\alpha_{12},\Upphi_{12}=-\alpha_{21}$ and $\Upphi_{22}=\alpha_{11}.$ Hence, the factor price of the economy reveals for factor 1 as

$$ \begin{aligned} \ln w_{1} &=\frac{1}{Det(\underline{\Upphi })}\sum\limits_{i=1}^{2}\Upphi_{i1}\cdot \ln \overline{p_{i}} \\ &=\sum\limits_{i=1}^{2}\frac{\Upphi_{i1}}{\Upphi }\ln A_{i}+\sum\limits_{i=1}^{2}\frac{\Upphi_{i1}}{\Upphi }\ln p_{i}+\frac{1}{\Upphi }\prod_{1=1}^{2}\left[\prod_{k=1}^{2}\alpha_{ik}^{\alpha_{ik}}\right]^{\Upphi_{i1}} \\ &=\sum\limits_{i=1}^{2}\beta_{i1}\ln A_{i}+\sum\limits_{i=1}^{2}\beta_{i1}\ln p_{i}+\gamma_{1} \end{aligned} $$

(45)

and for factor 2 as

$$ \begin{aligned} \ln w_{2} &=\frac{1}{Det(\underline{\Upphi })}\sum\limits_{i=1}^{2}\Upphi_{i2}\cdot \ln \overline{p_{i}} \\ &=\sum\limits_{i=1}^{2}\frac{\Upphi_{i2}}{\Upphi }\ln A_{i}+\sum\limits_{i=1}^{2}\frac{\Upphi_{i2}}{\Upphi }\ln p_{i}+\frac{1}{\Upphi }\prod_{1=1}^{2}\left[\prod_{k=1}^{2}\alpha_{ik}^{\alpha_{ik}}\right]^{\Upphi_{i2}} \\ &=\sum\limits_{i=1}^{2}\beta_{i2}\ln A_{i}+\sum\limits_{i=1}^{2}\beta_{i2}\ln p_{i}+\gamma_{2}. \end{aligned} $$

(46)

1.3 Cost functions of a M sector and N factor economy

Based on Eq. (15) the factor price ratios reveal as

$$ \frac{w_{k}}{w_{l}}=\frac{\alpha_{ik}}{\alpha _{il}}\frac{V_{il}}{V_{ik}}. $$

(47)

Thus, factor intensities are given by

$$ \frac{V_{il}}{V_{ik}}=\frac{w_{k}}{w_{l}}\frac{\alpha_{il}}{\alpha _{ik}}. $$

(48)

Reinserting the factor intensities (48) into Eq. (15) yields

$$ w_{k}=p_{i}A_{i}\alpha_{ik}\prod\limits_{j=1}^{n}\left( \frac{w_{k}}{w_{j}}\frac{\alpha_{ij}}{\alpha_{ik}}\right)^{\alpha _{ij}}. $$

(49)

With $\Uppi \alpha_{ik}^{\alpha_{ij}}=\alpha_{ik}^{\Upsigma\alpha_{ij}}=\alpha_{ik}$ and $\Uppi w_{k}^{\alpha i_{j}}=w_{k}^{\Upsigma \alpha_{ij}}=w_{k}$ the cost functions reveal as

$$ p_{i}=\frac{1}{A_{i}}\prod\limits_{j=1}^{n}\frac{w_{j}^{\alpha _{ij}}}{\alpha_{ij}^{\alpha_{ij}}}. $$

(50)

1.4 Determination of factor prices of a M sector and N factor economy

With $\ln w_{j}=\nu_{j}$ and $\ln \overline{p_{j}}=\eta _{j}$ the system (17) in matrix notation reveals as

$$ \underline{\Upphi}\underline{v}=\underline{\eta }. $$

(51)

$\underline{\Upphi}$ is the matrix with α − components, ν _j the unknowns and η _j the right hand side. The matrix $\underline{\Upphi}$ is nonsingular. Solving (51) by Cramer’s Rule yields

$$ \nu_{i}=\frac{1}{Det(\underline{\Upphi})}Det(\underline{\Upphi_{i}}). $$

(52)

Using $\underline{\Upphi}$ and substituting the ith-column by the right hand side of (51), denoting the result $\underline{\Upphi_{i}}$, it follows for case i = 1

$$ \ln w_{1}=\frac{1}{\det (\underline{\Upphi})}\det \left( \begin{array}{cccc} \ln \overline{p_{1}} & \alpha_{_{12}} &\ldots & \alpha_{_{1n}} \\ \ln \overline{p_{2}} & \alpha_{_{22}} &\ldots & \alpha_{_{2}n} \\ \ldots &\ldots &\ldots &\ldots \\ \ln \overline{p_{n}} & \alpha_{n2} &\ldots & \alpha_{nn} \end{array} \right). $$

(53)

Expansion of the first column yields

$$ \begin{aligned} \det (\underline{\Upphi})\ln w_{1} &=\ln \overline{p_{1}}\cdot \Upphi_{11}+\ln \overline{p_{2}}\cdot \Upphi_{21}+{\ldots}+\ln \overline{p_{n}}\cdot\Upphi_{n1}=\sum\limits_{i=1}^{n}\Upphi_{i1}\ln \overline{p_{i}} \\ \ln w_{1}^{\det (\underline{\Upphi})} &=\sum\limits_{i=1}^{n}\ln \overline{p_{i}}^{\Upphi_{i1}}. \end{aligned} $$

(54)

Hence, the general solution of the equation system (17) reveals as

$$ \det (\underline{\Upphi})\ln w_{j}=\ln \overline{p_{1}}\cdot \Upphi_{1j}+\ln\overline{p_{2}}\cdot \Upphi_{2j}+{\ldots}+\ln \overline{p_{n}}\cdot \Upphi_{nj}=\sum\limits_{i=1}^{n}\Upphi_{ij}\ln \overline{p_{i}}. $$

(55)

Rearranging (55) and denoting $\overline{p_{i}}=A_{i}p_{i}\prod\nolimits_{k=1}^{n}\alpha_{ik}^{\alpha _{ik}},\Upphi=\det (\underline{\Upphi}), \beta_{ij}=\Upphi_{ij}/\Upphi,\alpha_{j}=\prod\nolimits_{i=1}^{n}(\prod\nolimits_{k=1}^{n}\alpha_{ik}^{\alpha_{ik}})^{\Upphi_{ij}}$ and $\gamma_{j}=\frac{1}{\Upphi}\ln\alpha_{j}$ the factor prices of the economy reveal as

$$ \ln w_{j}=\gamma_{j}+\sum\limits_{i=1}^{n}\beta_{ij}\ln A_{i}+\sum\limits_{i=1}^{n}\beta_{ij}\ln p_{i}. $$

(56)