Models of Elastic Shells in Contact with a Rigid Foundation: An Asymptotic Approach

Abstract

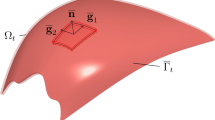
We consider a family of linearly elastic shells with thickness $2\varepsilon$ (where $\varepsilon$ is a small parameter). The shells are clamped along a portion of their lateral face, all having the same middle surface $S$, and may enter in contact with a rigid foundation along the bottom face.

We are interested in studying the limit behavior of both the three-dimensional problems, given in curvilinear coordinates, and their solutions (displacements $\boldsymbol{u}^{\varepsilon}$ of covariant components $u_{i}^{\varepsilon}$) when $\varepsilon$ tends to zero. To do that, we use asymptotic analysis methods. On one hand, we find that if the applied body force density is $O(1)$ with respect to $\varepsilon$ and surface tractions density is $O(\varepsilon)$, a suitable approximation of the variational formulation of the contact problem is a two-dimensional variational inequality which can be identified as the variational formulation of the obstacle problem for an elastic membrane. On the other hand, if the applied body force density is $O(\varepsilon^{2})$ and surface tractions density is $O(\varepsilon^{3})$, the corresponding approximation is a different two-dimensional inequality which can be identified as the variational formulation of the obstacle problem for an elastic flexural shell. We finally discuss the existence and uniqueness of solution for the limit two-dimensional variational problems found.