Hydrodynamics of a periodically wind-forced small and narrow stratified basin: a large-eddy simulation experiment

Abstract

We report novel results of a numerical experiment designed for examining the basin-scale hydrodynamics that control the mass, momentum, and energy distribution in a daily wind-forced, small thermally-stratified basin. For this purpose, the 3-D Boussinesq equations of motion were numerically solved using large-eddy simulation (LES) in a simplified (trapezoidal) stratified basin to compute the flow driven by a periodic wind shear stress working at the free surface along the principal axis. The domain and flow parameters of the LES experiment were chosen based on the conditions observed during summer in Lake Alpnach, Switzerland. We examine the diurnal circulation once the flow becomes quasi-periodic. First, the LES results show good agreement with available observations of internal seiching, boundary layer currents, vertical distribution of kinetic energy dissipation and effective diffusivity. Second, we investigated the wind-driven baroclinic cross-shore exchange. Results reveal that a near-resonant regime, arising from the coupling of the periodic wind-forcing ($T=24$ h) and the V2H1 basin-scale internal seiche ($T_{{\mathrm{V2H1}}}\approx 24$ h), leads to an active cross-shore circulation that can fully renew near-bottom waters at diurnal scale. Finally, we estimated the bulk mixing efficiency, $\varGamma$, of relevant zones, finding high spatial variability both for the turbulence intensity and the rate of mixing ($10^{-3}\le \varGamma \le 10^{-1}$). In particular, significant temporal variability along the slopes of the basin was controlled by the periodic along-slope currents resulting from the V2H1 internal seiche.

Appendices

Appendix 1: Observations in Lake Alpnach

Lakes that count with reliable hydrodynamic observations are excellent candidates for assessing the performance of numerical models. Simultaneously, numerical models are excellent tools to extend the understanding of these systems via exploratory numerical experiments. Lake Alpnach (Switzerland) is an extensively investigated system since late 80’s and is considered a real-scale laboratory to examine hydrodynamics and biogeochemical processes in lakes.

Fig. 14

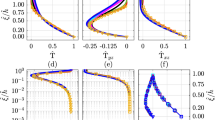
Field observations in Lake Alpnach. a Streamwise component of wind. b Streamwise velocity component (m s⁻¹) from ADCP at 31 m depth (adapted from Lorrai et al. [33]). c Arithmetic average of energy dissipation rate, $\varepsilon$, as a function of depth. $\epsilon$ was estimated from downward (circle marks) and upward (square marks) microstructure casts (adapted from Wüest et al. [79]). d Vertical eddy diffusivity, $K_{\rho }$, as a function of depth (adapted from Gloor et al. [19])

Figure 14 illustrates field observations of Lake Alpnach from different previous studies. Figure 14a, b shows the wind speed, $U_{10}$, and velocity component, u, along the main lake axis (streamwise axis in our coordinate system). Winds show a diurnal structure while the streamwise velocity component has a robust baroclinic signature compound by three- and four-layer patterns with maximum/minimum values of order $u\approx\, \pm\, 0.05$ m s⁻¹. This flow structure has been well-reproduced via a realistic RANS simulation by Lorrai et al. [33] and by our idealized LES experiment (see Fig. 3). Figure 14c, d shows the average kinematic energy dissipation rate, $\varepsilon$, as a function of depth based on temperature microstructure profiles [79] and the estimation of the vertical eddy diffusivity, $K_{\rho }$, in the interior basin based on tracer dispersion tracking [19, 20], respectively. The laterally/time-averaged energy dissipation and vertical eddy diffusivity estimated from our numerical simulations (Fig. 12b, h) show reasonable agreement not only in the vertical structure but also in magnitudes.

Appendix 2: Normal modes in a stratified trapezoidal basin

The oscillatory normal modes and their natural frequencies are constrained to the stratification, boundary conditions, and the basin topography. Here, we investigate the normal modes of our system for classifying the observed internal wave field. To do so, we solve the eigenvalue problem for the 2-D trapezoidal basin considering long wave approximation [18, 73]:

$$\begin{aligned} \frac{\partial ^{4}\psi }{\partial ^{2}t \partial ^{2}z} + N^{2}_{*}(z)\frac{\partial ^{2} \psi }{\partial x^{2}} =0, \end{aligned}$$

(16)

where $\psi$ is the stream function. The streamwise and the vertical velocity components are determined by $u=-\partial \psi /\partial z$ and $w=\partial \psi /\partial x$, respectively. In this case, $N_{*}$ is the background stratification profile at the beginning of the ninth period (Fig. 4a). To resolve (16), we further assume an inviscid fluid and null normal velocities at the boundaries. We look for modal structures of the form $\psi =\varPhi (x,z)e^{i\left( \omega t + \sigma \right) }$, where $\omega$ is the angular frequency of the mode and $\sigma$ an arbitrary wave phase. Then, Eq. (16) is reduced to

$$\begin{aligned} \frac{\partial ^{2}\varPhi }{\partial ^{2}x} - \frac{\omega ^{2}}{N^{2}_{*}(z)}\frac{\partial ^{2} \varPhi }{\partial z^{2}} =0. \end{aligned}$$

(17)

Equation (17) can be formulated as a generalized eigenvalue problem of the type $\mathbf A \varPhi = \omega ^{2}{} \mathbf B \varPhi$, where $\mathbf A$ is a matrix characterized by the discretization on the streamwise axis x and $\mathbf B$ is a matrix characterized by the discretization on the vertical axis z and $N^{2}_{*}(z)$. Resolving the above eigenvalue problem provides the 2-D spatial structure of the normal modes, $\varPhi (x,z)$, and their temporal structure established by $\omega$. Results are discussed in Sect. 3.1.