Thin-layer models for gravity currents in channels of general cross-section area, a review

Abstract

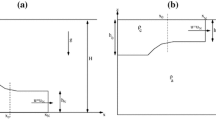
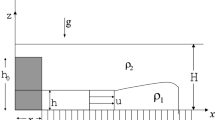
We present a brief review of the recent investigations on gravity currents in horizontal channels with non-rectangular cross-section area (such as triangle, $\bigvee$-valley, circle/semi-circle, trapezoid) which occur in nature (e.g., rivers) and constructed environment (tunnels, reservoirs, canals). To be specific, we discuss the propagation of a gravity current (GC) in a horizontal channel along the horizontal coordinate x, with gravity g acting in the $-z$ direction, and y the horizontal–lateral coordinate. The bottom and top of the channel are at $z=0,H$. The “standard” problem is concerned with 2D flow in a channel with rectangular (or laterally unbounded) cross-section area (CSA). Recent investigations have successfully extended the standard knowledge to the channels of CSA given by the quite general $-f_1(z)\le y \le f_2(z)$ for $0 \le z \le H$. This includes the practical $\bigvee$-valley, triangle, circle/semi-circle and trapezoid; these geometries may be in “up” or “down” setting with respect to gravity, e.g., $\bigtriangleup$ and $\bigtriangledown$. The major objective of the extended theory is to predict the height of the interface $z=h(x,t)$ and the velocity (averaged over the CSA) u(x, t), where t is time; the prediction includes the speed and position of the nose $u_N(t), x_N(t)$. We show that the motion is governed by a set of simplified equations, called “model,” that provides versatile and insightful solutions and trends. The emphasis in on a high-Reynolds-number current whose motion is dominated by buoyancy–inertia balance; in particular a GC released from a lock, which also contains general effects such as front and internal jumps (shocks), and reflected bore. We discuss two-layer, one-layer, and box models; Boussinesq and non-Boussinesq systems; compositional and particle-driven cases; and the effect of stratification of the ambient fluid. The models are self-contained, and admit realistic initial and boundary conditions. The governing equations are amenable to analytical solutions in some special circumstances. Some salient features of the buoyancy-viscous regime, and the estimate for the length at which transition to this regime takes place, are also presented. Some experimental support to the theory, and open questions for further investigations, are also mentioned. The major conclusions are (1) The CSA geometry has significant influence on the motion of the GC; and (2) The new theory is a useful, very significant, extension of the standard two-dimensional GC problem. The standard current is just a particular case, $f_{1,2} =$ constants, among many other covered by the new theory .

Appendices

Appendix 1: Energy dissipation of jump

The control-volume (CV) analysis of jumps in the two-layer system assumes that there is no shear on the boundaries of the CV. This includes free-slip on the channel walls, which also means zero vorticity there. However, shear is usually present inside the CV. This shear produces pressure head loss along stream lines, i.e., deviation from the ideal Bernoulli equation concerning conservation of $(1/2) u^2 + p/\rho + g z$ in steady-state circumstances. The global effect of the head loss is dissipation of mechanic energy inside the CV, into heat. The two-layer simplification poses restrictions on this effect; in particular, the head loss is z-independent for all streamlines of the same fluid that cross the CV (a stagnation streamline is an exception). Therefore, only two head-losses, $\delta _T^*$ and $\delta _B^*$ are present.

$\dot{\mathcal{D}}$ is defined as the rate of influx minus outflux of mechanic energy for a control volume attached to the jump, which in a realistic system must be positive or zero. In the simple jump flow (Sect. 2.2), the condition $\dot{\mathcal{D}} \ge 0$ determines, by a simple formula, the upper bound $\varphi _{\max }$ of the range of validity of $Fr_U, Fr_C$ formulas (see Sect. 2.2). The left-moving internal jump requires a more complicated calculation, as follows.

We use again the moving $S'$ system and a thin control volume attached to the jump, Fig. 6. The rate of dissipation of energy of the jump is defined as

$$\begin{aligned} \dot{\mathcal{D}} = \iint _{A_T} \left\{ \left[ \frac{1}{2}\rho {u'}^{\ 2} + \Pi + (\rho -\rho _{a})g z \right] u' \right\} _{in} d A - \iint _{A_T} \left\{ \left[ \frac{1}{2}\rho {u'}^{\ 2} + \Pi + (\rho -\rho _{a})g z \right] u' \right\} _{out} d A.\nonumber \\ \end{aligned}$$

(7.1)

The in and out subscripts are with respect to an observer inside the control volume (or up- and down-stream). The last term in the integrals represents the potential energy, because the pressure $\Pi$ is reduced with $+\rho _{a}g z$.

We use the same pressure terms and continuity equations as for the flow-force balance in Sect. 2.4.2. It turns out that the potential-energy terms cancel out with the $\Delta \rho gz$ terms of $\Pi$ on both sides of the jump. We can cast the balance (7.1), in dimensional form, as

$$\begin{aligned} \dot{\mathcal{D}} = A_0 \rho _{c}V_f\frac{1}{2}(V_f^2 - {u'_1}^{\,2}) + (A_T-A_0) \rho _{a}V_f\frac{1}{2}(V_f^2 - {u'_2}^{\,2}) + A_0 V_f\Delta \rho g (h_0-h_1) - A_T V_f\Pi _S^T . \end{aligned}$$

(7.2)

It can be shown (by elimination of the kinetic energy terms by (2.27)-(2.28)) that this result is identical with the sum of the fluxes of the head losses in the layers,

$$\begin{aligned} \dot{\mathcal{D}} = V_fg' \left[ A_0 \rho _{c}\delta _B^* + (A_T - A_0) \rho _{a}\delta _T^* \right] . \end{aligned}$$

(7.3)

This formula is evidently simple and insightful for the cases (a) $\delta _T^* =0$; and (b) $\delta _T^* = \delta _B^*$. In both cases, $\delta _B^* \ge 0$ is needed for validity.

The calculation of $\dot{\mathcal{D}}$ is performed after the solution of the jump, and hence $V_f$ and $h_1$ are known. For the $\delta _T^*=0$ case, $\Pi _S^T$ and $\delta _B^*$ are calculated from (2.27)-(2.28). For the $\delta _T^*= \delta _B^*$ case, $\Pi _S^T$ is calculated from (2.31); then $\delta _T^*$ is obtained from (2.27). Note that these equations can be simplified by the substitution $u_i' = K_i V_f$.

The dimensionless form of $\dot{\mathcal{D}}$ is obtained by Sect. 2.3 and scaling $\dot{\mathcal{D}}$ with $(1/2) \rho _{c}U^3 A_0$. This reads

$$\begin{aligned} \dot{\mathcal{D}} = \frac{2}{\varphi _0} V_f\left( \frac{1}{2}V_f^2 \left[ \varphi _0 (1 - K_1^2) + R (1-\varphi _0) (1 - K_2^2) \right] + \varphi _0 (1-h_1) - \Pi _S^T \right) . \end{aligned}$$

(7.4)

We noticed that there is some ambiguity concerning the distribution of the dissipation between the layers, i.e., the choice $\delta _T^*, \delta _B^*$. This topic requires further investigation. As indicated in Fig. 6, the upper fluid layer expands and the lower contracts, therefore $u_2' < u_1'$. If shear is present at the interface, in the lower layer there is speed reduction and energy loss (represented by $\delta _B^*>0$), while in the upper layer there is some speed increase and energy gain (represented by $\delta _T^*$). The 2D studies [4, 7, 44] indicate that in many cases of interest the positive $\delta _B^*$ dominates the energy balances. Therefore the suggestion (a) above is expected to capture well the total $\dot{\mathcal{D}}$ of the jump. Surprisingly, although $\delta _T^*$ is expected to be negative, various tests indicate that for a given system suggestion (b) above yields $V_f, h_1, \dot{\mathcal{D}}$ results close to these obtained with suggestion (a).

We reiterate that jumps are in general dissipative. The speed and height of the jump are determined by the “jump condition” (first equation) and matching with characteristics set by boundary-initial conditions (second equation). $\dot{\mathcal{D}}$ is a by-result, and the most we can do is to verify that it is non-negative. Consequently, in general, a valid SW gravity current system, with typically contains one or two jumps (each with $\dot{\mathcal{D}} \ge 0$), cannot be energy conserving. The direct detection of the dissipation effect is evasive. The typical heat production that can be associated with this dissipation is expected to cause only tiny temperature variations. Therefore, interestingly, the presence of dissipation is consistent with propagation of the jumps with constant speed over significant distances (the energy deficit is supplied by other domains of the system). There is no evident connection between the speed of propagation of the jump (or current) and $\dot{\mathcal{D}}$. The reliable means for dissipation evaluation is careful processing of Navier-Stokes simulation data (e.g. [4, 7]), but such calculations are not available for the non-rectangular CSA currents.

Appendix 2: The reflected bore

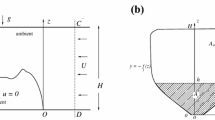
In flows of Type 2 and 3 (Fig. 5) the left-moving jump reaches the backwall $x=-1$ at time $t_f=1/V_f$, and is then reflected with speed $V_b$, which can be calculated as follows.

We recall that the left-moving jump activates the fluid at the right to the conditions: the height of the interface is $h_1$, and the velocities in the current and ambient are $u_1>0$ and $u_2<0$, respectively. We argue that at $t_f$ the “activated” ambient above the current hits the backwall with a significant speed, $|u_2|$. The wall stops this fluid abruptly, and hence the (reduced) pressure increases to $\Pi _L$, and the height of the interface is pushed down from $h_1$ to $h_{1L}$. The reflected jump thus has the conditions $h_1,u_1,u_2$ on the right, and $h_{1L}, 0, 0$ on the left. See Fig. 24.

To calculate the jump height $h_{**} = h_1 - h_{1L}$ and speed $V_b$ we use a system attached to the bore and moving with $V_b$ (to the right). The velocities $u_i$ in the laboratory system are transformed to $u'_i = u_i - V_b$. The additional subscript L is used to denote the variables in the left domain, between the wall and the reflected bore. Note that

$$\begin{aligned} u'_{1L}= u'_{2L} = - V_b. \end{aligned}$$

(8.1)

Continuity of volume fluxes gives

$$\begin{aligned} u'_{1L}A_{1L}= u'_1 A_1 \quad {\text {and}} \quad u'_{2L} (A_T - A_{1L}) = u'_{2} (A_T - A_1). \end{aligned}$$

(8.2)

Combining (8.1)–(8.2) yields

$$\begin{aligned} V_b= u_1 \frac{A_1}{A_1 - A_{1L}} = u_1 \frac{\varphi _1}{\varphi _1 - \varphi _{1L}}. \end{aligned}$$

(8.3)

The $\varphi$ variable is, again, the area ratio of current to total of the channel, $A_T$,

$$\begin{aligned} \varphi _{1j} = ( \int ^{h_{1j}}_0 f(z) dz ) / A_T, \end{aligned}$$

(8.4)

where $j = L$ or blank.

We recall that $u_1$ and $h_1$ (and hence, also $A_1$ and $\varphi _1$) are known from the dam-break solution. To determine $V_b$ we need only one additional value, $h_{1L}$. To this end we apply the momentum balances. The hydrostatic pressure, supplemented by Bernoulli’s equation on the streamline $z = H$, for the right and left sides of the jump read (dimensional)

$$\begin{aligned} \Pi _r= & {} \left\{ \begin{array}{ll} \mathcal {C}+ \Delta \rho g(h_1 - z) &{}\; \; (\text {over} \ A_1) \\ \mathcal {C}&{}\; \; (\text {over}\ A_T-A_1 ); \end{array} \right. \end{aligned}$$

(8.5)

$$\begin{aligned} \Pi _L= & {} \left\{ \begin{array}{ll} \mathcal {C}+ \frac{1}{2}\rho _a \left( u'^{\ 2}_2 - V_b^2 \right) + \Delta \rho g(h_{1L}-z) &{}\; \; (\text {over} \ A_{1L}) \\ \mathcal {C}+ \frac{1}{2}\rho _a \left( u'^{\ 2}_2 - V_b^2 \right) &{}\; \; (\text {over} \ A_T- A_{1L}) \end{array} \right. \end{aligned}$$

(8.6)

The x-momentum balance for a control volume about the jump is

$$\begin{aligned} \rho _{c}u'_1 A_1 (u'_1 - u'_{1L}) + \rho _{a}u'_2 (A_T- A_1) (u'_2 - u'_{2L}) = \iint _{A_T} \Pi _L dA - \iint _{A_T} \Pi _r dA. \end{aligned}$$

(8.7)

The LHS is the rate of change of momentum (outflux minus influx), and this is balanced by the pressure forces, expressed by the RHS. To simplify this equation, we substitute the above results for the pressure, express all velocities as multiples of $V_b$, employ the continuity relationships, scale the variables, and divide (8.7) by $A_T$. The result (dimensionless) is

$$\begin{aligned} &- \left[ u_1 \frac{\varphi _1}{\varphi _1 - \varphi _{1L}} \right] ^2 \left[ \varphi _{1L} (K_1 + 1) + R ( 1 - \varphi _{1L}) (K_2 + 1) + \frac{1}{2}R (K_2^ 2 - 1) \right] \nonumber \\ &\quad =h_{1L}\varphi _{1L} - h_1 \varphi _1 + \left(\int _{h_{1L}}^{h_1} z f(z) dz \right) / A_T, \end{aligned}$$

(8.8)

where $R = \rho _{a}/ \rho _{c}$, and

$$\begin{aligned} K_1 = - { \varphi _{1L} }/ { \varphi _1 }; \quad K_2 = - {( 1 - \varphi _{1L} ) } / {(1 - \varphi _1 )}. \end{aligned}$$

(8.9)

This is a general result for the reflected jump (bore) in a channel of cross-section-width function f(z), for both Boussinesq and non-Boussinesq systems. The numerical calculation of $h_{1L}$ from (8.8) is straightforward (we used a secant-method iteration); then $V_b$ is calculated by (8.3).

Fig. 24

Schematic description (in the laboratory frame) of the flow near the backwall, shortly after the formation of the reflected bore. The speed of the bore is $V_b$, and the depression of the interface due to the impingement of the ambient flow on the wall is $h_{**}$

Fig. 25

$V_b$ and $h_{**} = h_1 - h_{1L}$ of reflected bore as functions of H for various $\alpha$, $f(z) = z^\alpha$, in a Boussinesq system

Results for the power-law geometry are illustrated in Fig. 25 (the corresponding dam-break problem is considered in Sect. 2.7). We see that the strength of the reflected bore decreases when H and $\alpha$ increase. This is a straightforward consequence of the observation that the effect of the left-moving jump decreases in the same circumstances. In all the tested cases we found that $V_b/ V_f<1$, which could be expected. (In the rarefaction-wave limit, $V_b/ V_f= 1$).

Appendix 3: Box model

The “box model” is a simple tool for obtaining quick estimates for the global behavior of the GC, in particular $x_N, u_N$, mean thickness, and ratio of inertia to viscous forces, as functions of t. The effect of stratification in the ambient (parameter S) can be incorporated. For flows over a porous boundary, and for particle-driven currents, the box model may provide useful estimates of the “run-out” length and time. The flow-field of the current (or parts of it) are represented by bold simplifcations inspired by analogy with other cases, observation, expectation, insight, wishful-thinking, etc. The objective is to avoid the solution of the governing PDEs that emerge in the more rigorous SW or lubrication theories for the inertia-dominated and viscosity-dominated regimes, respectively. In general, these simplifications must be consistent at the kinematic level, and in accord with the major boundary conditions, in particular: volume conservation, spread-out of $x_N$, influx at $x=0$ (when present), particle settling (or drainage) at the bottom for particle-driven currents (or over a porous boundary). The major simlification is that a simple interface is postulated, usually a horizontal $h=h(t)$ (fully or piecewise), and the nose front $x=x_N(t)$ is a vertical line. In many case of interest the entire CG is considered a horizontal box (a quite unrealistic representation, except for some constant-influx currents). Various other simlifications can be incorporated, such as an x-independent volume fraction in particle-driven currents, constant Fr, and energy-conserving jumps. Then, a momentum-integral type of approach, which considers balances over the entire control volume of the GC can be applied. The advantage over the SW (or lubrication) formulation is that the box-model balances express the dependent variables ($h, x_N, u_N$, etc.) in terms of initial-conditions ODEs that can be integrated by standard numerical methods (like Runge-Kutta), sometimes by quadratures (like Romberg), or even analytically.

The box-shape actually introduces a similarity assumption into the problem. The $h=h(t)$ interface implies a linear $u(x,t) = a(t) + b(t) x$, see the continuity equation (2.15). Since the rigorous thin-layer formulations admit similarity solutions in some circumstances, this box model can be regarded as an approximation, or extrapolation, to the self-similar propagation feature. In any case, we must keep in mind that this tool lacks rigor and should be used with care. The box description may produce the illusion that the GC is governed by kinematic effects: the vertical nose moves and the current follows due to continuity. Indeed, a horizontal interface implies $\partial p / \partial x = 0$ for a deep current, see (3.5), i.e., the entire bouyancy (pressure gradient) effect is concentrated at the vertical nose. This is unrealistic, because usually the inertial currents in developed stage have $\partial p / \partial x > 0$ (positive inclination); while viscous currents need $\partial p / \partial x <0$ (negative inclination) to overcome the shear see (4.4)–(4.5), and end up with $h_N =0$. The $h=h(t)$ interface implies equidistribution of the mass, and potential energy, over $x_N$, which is also an oversimplification. The absence of characteristics in the box model equations allows presence of unrealistic jumps (e.g. supercritical, unstable or unneeded) in the solution. We cannot expect much physical accuracy from a flow-field prediction which uses such components. Whenever the box-model results are in disagreement with the thin-layer (SW or lubrication) predictions in the range of validity, the latter prevail.

Here we consider in some detail high-Reynolds Boussinesq $\rho _{a}/\rho _{c}\approx 1$ GCs. We show that a significant extension of the standard 2D case to general f(z) is available.

For the high-Reynolds GC the main dynamics of propagation is usually attributed to the jump condition $u_N = Fr (g' h) ^{1/2}$. The interaction between the body and the nose $u_N$ is kinematic: h changes due to propagation (and influx or porous-bottom drain when present) and $g'$ changes due to settling in particle-driven currents. However, the box model does not contain characterisitcs and hence effects like dam-break development, presence/absence of internal jumps, and critical $u_N$ cannot be detected. If relevant, such effects must be incorpoarated as ad-hoc additions to the box-model equations.

1.1 Constant $\rho _{c}$ current

Here we consider the compositional current, in a linearly stratified ambient expressed by the parameter S, see (3.2). The homogeneous ambient is recovered by $S=0$.

The motion is governed by the total volume conservation and a front-speed condition. Using (3.7)–(3.8) and (3.10) we obtain the two governing equations of the box model, in dimensionless form, as follows

$$\begin{aligned} x_N= & {} \frac{\mathcal {V}}{A(h)} ; \end{aligned}$$

(9.1)

$$\begin{aligned} \frac{d x_N}{dt}= & {} u_N = Fr_U (h) \, h ^{1/2} \left[ 1 -S + \frac{1}{2}S \frac{h}{H} ( 1 + \gamma ) \right] ^{1/2}, \end{aligned}$$

(9.2)

where $\mathcal {V}= \mathcal {V}(t)$ is the prescribed volume of the current, Fr and $\gamma$, see (2.12) and (3.10), usually depend on h. A(h) is the area of the current, and in general by (9.1) h(t) can be calculated when $\mathcal {V}(t)$ and $x_N(t)$ are known. Note that

$$\begin{aligned} \frac{d x_N}{dt} = -\frac{\mathcal {V}}{A^2} f(h) \frac{d h }{dt} + \frac{1}{A} \frac{d \mathcal {V}}{dt}. \end{aligned}$$

(9.3)

The numerical calculation of $x_N,h$ with given initial $h, x_N$ can be performed.

For $\mathcal {V}= q t$, the solution is the slug-like constant $h, u_N$, determined by $A(h) u_N(h) = q$. This can be verified by substitution into (9.1)–(9.3). However, more reliable slug-like results can be obtained directly from the SW formulation, see Sect. 3.4.1.

For constant $\mathcal {V}$, the solution can be simplified by combining (9.1)–(9.3) into

$$\begin{aligned} \frac{d h}{dt} = - \frac{1}{\mathcal {V}} Fr_U(h) \, h ^{1/2}\frac{A^2(h)}{f(h)} \left[ 1 -S + \frac{1}{2}S \frac{h}{H} ( 1 + \gamma ) \right] ^{1/2}= - \mathcal {G}(h). \end{aligned}$$

(9.4)

Formal integration, with the initial condition $h(t=0)=1$, yields

$$\begin{aligned} t = \int _{h(t)}^1 \frac{d h'}{\mathcal {G}(h')}, \end{aligned}$$

(9.5)

which gives, implicitly, h(t). Next, we substitute h(t) into (9.1) to produce $x_N(t)$. Note that, in scaled form, $\mathcal {V}= A(1)$; therefore (9.1) can be rewritten as $x_N = A(1)/A[h(t)]$. Analytical integration is convenient when the conditions (1) a power-law $f(z) = z^\alpha$ cross-section, (2) a constant Fr, and (3) $S=1$ or $S=0$, are combined. Under these conditions the $\mathcal {G}(h)$ function is simple, of the form $C h^p$ where p is a constant depending on $\alpha$ and S. In this case the box model yields the analytical result, $x_N(t) = K_1 ( t + c )^\beta$, where the power $\beta$ is the same as for the self-similar solution for the corresponding S, see Sect. 3.4. The constants $K_1$ and c are determined by the initial conditions.

When the box model is used for $H=1$ (or close), an artificially adjusted Fr must be used, because the theoretical Fr formulas are invalid, and yield very small values, for the initial situation $h_N/H \approx 1$. A plausibe approximation is $Fr(\varphi _{\max })$ for $\varphi \ge \varphi _{\max }$. In any case, the initial motion is not a good approximation of the correct slumping phase.

Figure 26 compares the propagation predicted by the SW one-layer solution and box model, for two cross section geometries. The box model first overpredicts, then underpredicts, the speed of propagation, but, overall, in the tested cases it provides $x_N(t)$ in fair agreement with the SW solution. The influence of the stratification parameter S is correctly reproduced. However, we must keep in mind that the box model does not reproduce the initial slumping stage with constant speed.

1.1.1 Energy budget

Consider a box-current of fixed $\mathcal {V}$. The simple $h=h(t)$ and linear $u = u_N x/x_N$ in the current (accompanied by $u_a = - u \varphi /(1-\varphi )$ in the ambient) facilitate the calculation of potential, kinetic, and total energy (P, K, E) of the two-fluid system as functions of t. We use dimensional variables, and recall $\rho _a \approx \rho _c$. The potential energy is due to work needed for the elevation of dense particles in the hydrostatic pressure field of the ambient to height z, and can be expresses as

$$\begin{aligned} P(t) = \rho _{c}g' x_N \int _0^{h} \left[ (1 -S) z + \frac{1}{2}\frac{S}{H} z^2 \right] f(z) dz = \rho _{c}g' \mathcal {V}\left[ \frac{1}{2}(1-S) \tilde{h} + \frac{S}{6 H} \hat{h}^2 \right] \end{aligned}$$

(9.6)

where

$$\begin{aligned} \tilde{h} = 2 \int _0^h z f(z) dz / A; \quad \hat{h}^2 = 3 \int _0^h z^2 f(z) dz / A. \end{aligned}$$

(9.7)

The details for the force-potential terms used above is given in [36] §20.2. $A = A(h)$ is the area of the current. Note that $\tilde{h},\hat{h}$ are of the order of magnitude of h; for the 2D case, $\tilde{h}=\hat{h} = h$. P(t) decreases with t, as expected, because $h, \tilde{h}, \hat{h}$ decrease while $x_N$ increases.

The kinetic energy of the box-system is

$$\begin{aligned} K(t)& {}= \rho _{c}x_N A \int _0^{x_N} \frac{1}{2}(u^2 + u_a^2 \frac{1-\varphi }{\varphi }) dx = \frac{1}{\displaystyle 6} \rho _{c}\mathcal {V}u_N^2 \frac{1}{1-\varphi (h)} \nonumber \\& {}= \frac{1}{\displaystyle 6} \rho _{c}\mathcal {V}\frac{Fr_U^2 [ 1-S + Sh (1 + \gamma )/(2 H)], }{1-\varphi (h)} g' h. \end{aligned}$$

(9.8)

where (9.2) was used for the last term. In a realistic system the kinetic energy develops from zero during the dam-break stage, but in the simple box-model current there is motion, and significant kinetic energy, from the beginning.

With $h,u_N$ calculated by (9.5) and (9.2), we can evaluate the energy budget $E = P+K$ as a function of t. In all tested cases we detected dissipation: E(t) is a monotonic decreasing function, because $h, \tilde{h}, \hat{h}$ decrease while $x_N$ increases. The $Fr_U^2/(1-\varphi )$ coefficient of the kinetic energy term increases, but this compensation is too small for changing the trend of clear-cut energy dissipation. Furthermore, a different trend is not physical. Suppose that energy is conserved, $K(t) + P(t) = E(0)$ = const. Using (9.8) we obtain, after some algebra

$$\begin{aligned} u_N^2 = 6 \left[ E(0) - P(t) \right] \left[ 1 - \varphi (h) \right] /(\rho _{c}\mathcal {V}) \end{aligned}$$

(9.9)

The RHS term is positive and increases with time, because $P(t), \varphi (h)$ decrease with t to 0. Therefore, the energy-conserving GC is expected to accelerate during the main inertial propagation. The sustained increase of $u_N$ in a fixed-volume propagation contradicts all known SW predictions, and physical observations. This indicates that the energy-conserving GC system is an unacceptable concept. The present conclusion applies to a general f(z) and thus extends the counterpart result for the 2D current; see [36] §5.5.3.3.

1.2 Particle-driven current

The box model is useful for Boussinesq dilute monodisperse particle-driven currents; see e.g. [26, 47]. The scaling and definitions are given in Sect. 3.5. We assume homogeneous ambient, $S=0$. In the T-model (turbulent mixing of the particles, see [36] §9.1.2), the volume $\mathcal {V}$ of the current is constant, and (9.1) is valid. We postulate that the volume fraction of the particles, $\phi$, depends on t only. $\phi$ decreases due to settling over the area below the interface $\max [f(0),f(h)] x_N$. For simplicity, we consider monotonic changes of f(z). We obtain

$$\begin{aligned} \mathcal {V}\frac{d \phi }{dt} = -\beta \phi \, (\max [f(0), f(h)] \, x_N). \end{aligned}$$

(9.10)

The front propagation takes into account the dependency of $g'$ on $\phi$, and reads

$$\begin{aligned} \frac{d x_N}{dt} = Fr (h) \phi ^{1/2} \, h ^{1/2}. \end{aligned}$$

(9.11)

With the initial conditions $\phi = h = x_N=1$, the time-dependent $x_N$ and $\phi$ can be calculated from (9.1), (9.10)–(9.11). We recall that the settling coefficient $\beta$ is small. For the power-law $f(z)= b z^\alpha$ and constant Fr, a versatile analytical result can be obtained, which shows that the particles-run-out distance is proportional to $\beta$ at the power $-(2 \alpha + 2)/(2 \alpha + 5)$. The expansion of the CSA (increase of $\alpha$) yields a faster current, and hence a longer propagation until the particles settle out. This trend is in agreement with the more rigorous SW solutions, and with experimental data; see Sect. 3.5.

The box-model can be extended to currents with particles of different sizes and densities, i.e., several settling parameters $\beta _j$ and volume fractions $\phi _j$. For each component we write the conservation Eq. (9.10), while $g'$ (represented by $\phi$ in Eq. (9.11)) is calculated according to the density of the combined components. Such an extension is presented in [23, 24] for gravity currents of bi- and poly-disperse suspensions in a $\bigvee$-valley tank.

Fig. 26

Comparison of SW (solid line) and box-model (dash-dot line) $x_N$ as a function of t for various S, $H=2$. Left circle $f(z) = 2 [2 z(2 -z/2)]^{1/2}$; right trapezoid $f(z) = (1+z)/2$

1.3 Lock-exchange

The typical box model of Sect. 9.1, for a fixed $\mathcal {V}$ current released form a lock at $t=0$, predicts in general a time decaying $u_N$ for $t>0$. As $x_N$ increases, h is bound to decrease, and hence $u_N \propto h^{1/2}$ decreases. (Although $Fr_U$ increases when h decreases, the $h^{1/2}$ term was dominant in all tested cases). This contradicts the well-known constant $u_N$ slumping behavior that typifies the dam-break flow, and in particular the lock-exchange configuration. The dam-break and slumping solution are governed by characteristics from the reservoir (lock) and from the dam (gate). The general box model lacks this mechanism, and hence a special set of assumptions is needed to reproduce the missed effect.

The dam-break (lock-exchange) $H=1, S=0$ simplified model uses the $h=h_N$ assumption, and adds the postulates that $u_N$ is constant (time-independent), and the nose is non-dissipative with $\varphi _N = \varphi _{\max }$ [12, 20]. While the first postulate is consistent with the SW predictions, the second violates the SW result that the front $u_N$ is critical, and dissipative. The propagation solution is obtained simply by solving (see Sect. 2.2) the zero-dissipation condition $Fr_U^2(\varphi _{\max }) = 2(1-\varphi _{\max })^2$; this $\varphi _{\max }$ provides the thickness $h_N$ of the current, then $u_N= \sqrt{2} (1-\varphi _{\max }) (g' h_N)^{1/2}$. This $u_N$ is in fair agreement with experiments reported in these papers. However, as mentioned in Sect. 3.2, the one-layer SW theory also provides simple similar $u_N$ results for this case, without the need for these postulates. Also note that only for the 2D case form the upper and lower currents of the $H=1$ box solution a continuous lock-exchange pair. In general, as noted by [20], the thickness $h_1$ (scaled with $h_0$) of the lower energy-conserving layer (that propagates to the right of the gate) is different from $h_2$ of the upper layer that propagates to the left of the gate, and $h_1 + h_2 \ne H =1$. For the triangle $f(z) = z$, the energy-conserving $h_1 = 0.577$ while $h_2 = 0.320$. Since $h_1 + h_2 = 0.897 \ne H =1$, some additional jump is needed to match the lower and upper currents in the box. The more rigorous SW solution, see Table 1 and Fig. 11, clarifies the situation.

Jones et al. [12] developed, and tested, an extension of the $H=1$ box model for up-slope propagation in a $\bigvee$ tank, but this system is beyond the scope of the present paper.