Skip to main content
SpringerLink
Log in

Turbulent entrainment into fluid mud gravity currents

  • Original Article
  • Published:
Environmental Fluid Mechanics Aims and scope Submit manuscript

Abstract

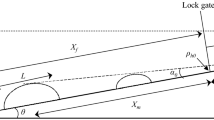
The entrainment of ambient water into non-Newtonian fluid mud gravity currents was investigated in this study. Constant volume release gravity currents were generated in a lock-exchange tank for a wide range of experimental conditions. A technique similar to the so-called light attenuation technique was used to find the boundary of the current, allowing for the calculation of both temporal and bulk entrainment parameters (in terms of the temporal and bulk entrainment velocities, respectively). It was found that the temporal entrainment velocity is dependent on different parameters in the different propagation phases. The slumping phase begins with an adjustment zone (henceforth, non-established zone) in which the temporal entrainment velocity is not a function of the current front velocity, followed by the established zone in which the temporal entrainment velocity is a function of the current front velocity. This dependence of the temporal entrainment velocity on the current front velocity carries through to the inertia-buoyancy phase. As expected, temporal entrainment velocity in the viscous-buoyancy phase was negligible in comparison to average entrainment velocity in the other phases. It is observed that the temporal entrainment characteristics in the non-established zone is governed by the competition between the entrainment-inhibiting density stratification effects and the entrainment-favouring effects of the Kelvin–Helmholtz billows that are quantified by the Richardson number and the Reynolds number of the gravity current, respectively. In the established zone, Reynolds number effects were observed to dominate over Richardson number effects in dictating temporal entrainment characteristics. A parameterization for the temporal entrainment velocity for non-Newtonian fluid mud gravity currents is developed based upon the experimental observations. This study also found that the bulk entrainment characteristics for the non-Newtonian fluid mud gravity currents can be parameterized by the Newtonian bulk entrainment parameterizations that rely solely on a bulk Richardson number. Interestingly, it was found that the non-Newtonian characteristics of the gravity current have little to no effect on the entrainment of the Newtonian ambient fluid.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15

Similar content being viewed by others

References

  1. Bonnecaze R, Huppert H, Lister J (1993) Particle-driven gravity currents. J Fluid Mech 250:339–339

    Google Scholar 

  2. Breidenthal RE (1992) Entrainment at thin stratified interfaces: the effects of Schmidt, Richardson, and Reynolds numbers. Phys Fluids A 4(10):2141–2144

    Article  Google Scholar 

  3. Britter R, Simpson J (1978) Experiments on the dynamics of a gravity current head. J Fluid Mech 88:223–240

    Article  Google Scholar 

  4. Cantero MI, Lee JR, Balachandar S, Garcia MH (2007) On the front velocity of gravity currents. J Fluid Mech 586:1–39

    Article  Google Scholar 

  5. Cantero MI, Balachandar S, Garcia MH, Bock D (2008) Turbulent structures in planar gravity currents and their influences on the flow dynamic. J Geophy Res 113:C08018

    Google Scholar 

  6. Cenedese C, Adduce C (2010) A new parameterization for entrainment in overflows. J Phys Oceanogr 40:1835–1850

    Article  Google Scholar 

  7. Cenedese C, Dalziel SB (1998) Concentration and depth fields determined by the light transmitted through a dyed solution. In: Carlomagno GM, Grant I (eds) Proc. 8th Intl Symp. On Flow Visualization, Paper 061. ISBN 0953399109

  8. Chowdhury MR, Testik FY, Khan AA (2009) Three-dimensional flow structure at the frontal zone of a gravity-driven fluid mud flow. J Vis 12(4):287

    Article  Google Scholar 

  9. Chowdhury MR, Testik FY (2011) Laboratory testing of mathematical models for high-concentration fluid mud turbidity currents. Ocean Eng 38(1):256–270

    Article  Google Scholar 

  10. Di Federico V, Malavasi S, Cintoli S (2006) Viscous propagation of non-Newtonian gravity currents on a plane. Meccanica 41:207–217

    Article  Google Scholar 

  11. Ellison TH, Turner JS (1959) Turbulent entrainment in stratified flows. J Fluid Mech 6:423–448

    Article  Google Scholar 

  12. Felix M (2002) Flow structure of turbidity currents. Sedimentology 49:397–419

    Article  Google Scholar 

  13. Fernando HJS (1991) Turbulent mixing in stratified fluids. Annu Rev Fluid Mech 23:455–493

    Article  Google Scholar 

  14. Garcia MC, Parsons JD (1996) Mixing at the front of gravity currents. Dyn Atmos Oceans 24:197–205

    Article  Google Scholar 

  15. Hacker J, Linden PF, Dalziel SB (1996) Mixing in lock-release gravity currents. Dyn Atmos Oceans 24:183–195

    Article  Google Scholar 

  16. Hallworth MA, Phillips JC, Huppert HE, Sparks RSJ (1993) Entrainment in turbulent gravity currents. Lett Nat 362:829–831

    Article  Google Scholar 

  17. Hallworth MA, Huppert HE, Phillips JC, Sparks RSJ (1996) Entrainment into two-dimensional and axisymmetric turbulent gravity currents. J Fluid Mech 308:289–311

    Article  Google Scholar 

  18. Hartel C, Meiburg E, Necker F (2000) Analysis and direct numerical simulation of the flow at a gravity-current head. Part 1. Flow topology and front speed for slip and no-slip boundaries. J Fluid Mech 418:189–212

    Google Scholar 

  19. Huang X, Garcia M (1998) A Herschel-Bulkley model for mud flow down a slope. J Fluid Mech 374:305–333

    Article  Google Scholar 

  20. Huppert HE, Simpson JE (1980) The slumping of gravity currents. J Fluid Mech 99:785–799

    Article  Google Scholar 

  21. Huppert H (2006) Gravity currents: a personal perspective. J Fluid Mech 554:299–322

    Article  Google Scholar 

  22. Jacobson MR, Testik FY (2013) On the concentration structure of high-concentration constant-volume fluid mud gravity currents. Phys Fluids 25:016602

    Article  Google Scholar 

  23. Kneller B, Buckee C (2000) The structure and fluid mechanics of turbidity currents: a review of some recent studies and their geological implications. Sedimentology 47:62–94

    Article  Google Scholar 

  24. Kranenburg C, Winterwerp JC (1997) Erosion of fluid mud layers. I: entrainment model. J Hydraul Eng 123(6):504–511

    Article  Google Scholar 

  25. Mehta AJ (1989) On estuarine cohesive sediment suspension behavior. J Geophys Res 94:14303–14314

    Article  Google Scholar 

  26. Middleton G (1993) Sediment deposition from turbidity currents. Annu Rev Earth Planet Sci 21:89–114

    Article  Google Scholar 

  27. Morton B, Taylor G, Turner J (1956) Turbulent gravitational convection from maintained and instantaneous sources. Proc R Soc London 268:283–292

    Google Scholar 

  28. Neal R, Henry G, Greene S (1978) Evaluation of the submerged discharge of dredged material slurry during pipeline dredge operations. TR D-78-44, US Army Engineers Waterways Experiment Station, Vicksburg, Mississippi, p 176

  29. Newell RC, Seiderer LJ, Hitchcock DR (1998) The impact of dredging works in coastal waters: a review of the sensitivity to disturbance and subsequent recovery of Biological resources on the sea bed. Oceanogr Mar Biol Annu Rev 36:127–178

    Google Scholar 

  30. Ng C, Mei C (1994) Roll waves on a shallow layer of mud modelled as a power-law fluid. J Fluid Mech 263:151–183

    Article  Google Scholar 

  31. Nichols M, Thompson G, Faas R (1978) A field study of fluid mud dredged material: its physical nature and dispersal. TR D-78-40, US Army Engineers Waterways Experiment Station, Vicksburg, Mississippi, p 91

  32. Nogueira HIS, Adduce C, Alves E, Franca MJ (2013) Dynamics of the head of gravity currents. Environ Fluid Mech. doi:10.1007/s10652-013-9315-2

  33. Parker G, Garcia MH, Fukushima Y, Yu W (1987) Experiments on turbidity currents over an erodible bed. J Hydraul Res 25:123–147

    Article  Google Scholar 

  34. Parsons JD, Garcia MH (1998) Similarity of gravity current fronts. Phys Fluids 10:3209–3213

    Article  Google Scholar 

  35. Peng M, Lee CB (2010) Frontal instability of lock-exchange gravity currents. Mod Phys Lett B 24:1369–1372

    Article  Google Scholar 

  36. Princevac M, Fernando HJS, Whiteman CD (2005) Turbulent entrainment into natural gravity driven flows. J Fluid Mech 533:259–268

    Article  Google Scholar 

  37. Rottman J, Simpson J (1983) Gravity currents produced by instantaneous releases of a heavy fluid in a rectangular channel. J Fluid Mech 135:95–110

    Article  Google Scholar 

  38. Simpson J (1997) Gravity currents: in the environment and the laboratory. Cambridge University Press, Cambridge

    Google Scholar 

  39. Simpson J, Britter R (1979) The dynamics of the head of a gravity current advancing over a horizontal surface. J Fluid Mech 94:477–495

    Article  Google Scholar 

  40. Teeter A (2002) Sediment Dispersion near dredge pipeline discharge in Laguna Madre, Texas. Technical Note DOER-N-16, US Army Engineer Waterways Experiment Station, Vicksburg

  41. Turner JS (1979) Buoyancy effects in fluids, 2nd edn. Cambridge University Press, Cambridge

    Google Scholar 

  42. Turner JS (1986) Turbulent entrainment: the development of the entrainment assumption, and its application to geophysical flows. J Fluid Mech 173:431–471

    Article  Google Scholar 

  43. Ungarish M (2009) An introduction to gravity currents and intrusions. Chapman and Hall, Boca Raton

    Book  Google Scholar 

  44. Van Kessel T, Kranenburg C (1996) Gravity current of fluid mud on sloping bed. J Hydraul Eng 123:710–717

    Article  Google Scholar 

  45. Whitehouse R, Soulsby R, Roberts W, Mitchener H (2000) Dynamics of estuarine muds: a manual for practical applications. Thomas Telford, London, p 209

    Book  Google Scholar 

  46. Winterwerp J, Kesteren WV (2004) Introduction to the physics of cohesive sediment in the marine environment. Elsevier, Amsterdam, p 466

    Google Scholar 

Download references

Acknowledgments

This research was partially supported by the funds provided by the USACE Grant W912HZ-09-C-0068 to the second author (F. Y. Testik). The first author (M. R. Jacobson) is a Master of Science student under the guidance of F. Y. Testik. We would also wish to express our gratitude to Ms. Crystal Bassett for her assistance in the laboratory.

Author information

Authors and Affiliations

  1. Glenn Department of Civil Engineering, College of Engineering and Science, Clemson University, 110 Lowry Hall, Clemson, SC, 29634-0911, USA

    M. R. Jacobson & F. Y. Testik

Authors
  1. M. R. Jacobson
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. F. Y. Testik
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to F. Y. Testik.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Jacobson, M.R., Testik, F.Y. Turbulent entrainment into fluid mud gravity currents. Environ Fluid Mech 14, 541–563 (2014). https://doi.org/10.1007/s10652-014-9344-5

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10652-014-9344-5

Keywords

Search

Navigation