Abstract
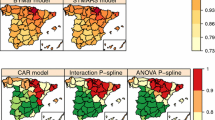
Smoothing risks is one of the main goals in disease mapping as classical measures, such as standardized mortality ratios, can be extremely variable. However, smoothing risks might hinder the detection of high risk areas, since these two objectives are somewhat contradictory. Most of the work on smoothing risks and detection of high risk areas has been derived using conditional autoregressive (CAR) models. In this work, penalized splines (P-splines) models are also investigated. Confidence intervals for the log-relative risk predictor will be derived as a tool to detect high-risk areas. The performance of P-spline and CAR models will be compared in terms of smoothing (relative bias), sensitivity (ability to detect high risk areas), and specificity (ability to discard false patterns created by noise) through a simulation study based on the well-known Scottish lip cancer data.
Similar content being viewed by others
References
Besag J (1974) Spatial interaction and the statistical analysis of lattice systems (with discussions). J R Stat Soc Ser B 36: 192–236
Besag J, York J, Mollié A (1991) Bayesian image restoration with two applications in spatial statistics. Ann Inst Stat Math 43: 1–59
Breslow NE, Clayton DG (1993) Approximate inference in generalized linear mixed models. J Am Stat Assoc 88: 9–25
Clayton DG, Kaldor J (1987) Empirical Bayes estimates of age-standardized relative risks for use in disease mapping. Biometrics 43: 671–681
Currie ID, Durbán M, Eilers PH (2004) Smoothing and forecasting mortality rates. Stat Model 4: 279–298
Dean CB, Ugarte MD, Militino AF (2001) Detecting interaction between random region and fixed age effects in disease mapping. Biometrics 57: 197–202
Dean CB, Ugarte MD, Militino AF (2004) Penalized quasi-likelihood with spatially correlated data. Comput Stat Data Anal 45: 235–248
Eilers PHC, Marx BD (1996) Flexible smoothing with B-splines and penalties. Stat Sci 11: 89–121
Eilers PHC, Currie ID, Durbán M (2006) Fast and compact smoothing on large multidimensional grids. Comput Stat Data Anal 50: 61–76
Harville DA (1977) Maximum likelihood approaches to variance component estimation and to related problems. J Am Stat Assoc 72: 320–340
Lawson AB (2009) Bayesian disease mapping. Hierarchical modelling in spatial epidemiology. Chapman and Hall, Boca Raton
Lee D-J, Durbán M (2009) Smooth-CAR mixed models for spatial count data. Comput Stat Data Anal 53: 2968–2979
Leroux BG, Lei X, Breslow N (1999) Estimation of disease rates in small areas: a new mixed model for spatial dependence. In: Halloran ME, Berry D (eds) Statistical models in epidemiology, the environment and clinical trials. Springer, New York, NY, pp 179–192
Liang F, Lui C, Carroll RJ (2010) Advanced Markov chain Monte Carlo methods. Wiley, Chichester
Lin X (2007) Estimation using penalized quasilikelihood and quasi-pseudo-likelihood in Poisson mixed models. Lifetime Data Anal 13: 533–544
MacNab YC (2003) Hierarchical Bayesian modelling of spatially correlated health service outcome and utilization of rates. Biometrics 59: 305–316
MacNab YC, Dean CB (2000) Parametric bootstrap and penalized quasi-likelihood inference in conditional autoregressive models. Stat Med 19: 2421–2435
MacNab YC, Dean CB (2001) Autoregressive spatial smoothing and temporal spline smoothing for mapping rates. Biometrics 57: 949–956
MacNab YC, Gustafson P (2007) Regression B-spline smoothing in Bayesian disease mapping: with an application to patient safety surveillance. Stat Med 26: 4455–4474
MacNab YC, Farrel PJ, Gustafson P, Wen S (2004) Estimation in Bayesian disease mapping. Biometrics 60: 865–873
MacNab YC, Kmetic A, Gustafson P, Sheps S (2006) An innovative application of Bayesian disease mapping methods to patient safety research: a Canadian adverse medical event study. Stat Med 25: 3960–3980
Militino AF, Ugarte MD, Dean CB (2001) The use of mixture models for identifying high risks in disease mapping. Stat Med 20: 2035–2049
Opsomer JD, Claeskens G, Ranalli MG, Kauermann G, Breidt FJ (2008) Non-parametric small area estimation using penalized spline regression. J R Stat Soc B 70: 265–286
Perperoglou A, Eilers PH (2010) Penalized regression with individual deviance effects. Comput Stat 25: 341–361
R Development Core Team (2010) R: A language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria. http://www.r-project.org/
Richardson S, Thomson A, Best N, Elliot P (2004) Interpreting posterior relative risk estimates in disease-mapping studies. Environ Health Perspect 112: 1016–1025
Richardson S, Abellán JJ, Best N (2006) Bayesian spatio-temporal analysis of joint patterns of male and female lung cancer risks in Yorkshire. Stat Methods Med Res 15: 385–407
Ruppert D (2002) Selecting the number of knots for penalized splines. J Comput Graph Stat 11: 735–757
Schall R (1991) Estimation in generalized linear models with random effects. Biometrika 78: 719–727
Spiegelhalter DJ, Thomas A, Best NG, Lunn DJ (2003) WinBUGS version 1.4 user’s manual. MRC Biostatiscs unit. Institute of Public Health, Cambridge; Rolf Nevanlinna Institute, University of Helsinki; and Department of Epidemiology and Public Health, Imperial College London. http://www.mrc-bsu.cam.ac.uk/bugs
Tango T (2010) Statistical methods for disease clustering. Springer, New York, NY
Ugarte MD, Ibáñez B, Militino AF (2005) Detection of spatial variation in risk when using CAR models for smoothing relative risks. Stoch Environ Res Risk Assess 19: 33–40
Ugarte MD, Militino AF, Goicoa T (2008) Prediction error estimators in empirical Bayes disease mapping. Environmetrics 19: 287–300
Ugarte MD, Goicoa T, Militino AF (2009a) Empirical Bayes and fully Bayes procedures to detect high-risk areas in disease mapping. Comput Stat Data Anal 53: 2938–2949
Ugarte MD, Goicoa T, Ibáñez B, Militino AF (2009b) Evaluating the performance of spatio-temporal Bayesian models in disease mapping. Environmetrics 20: 647–665
Wakefield J (2007) Disease mapping and spatial regression with count data. Biostatistics 8: 158–183
Waller LA, Gotway CA (2004) Applied spatial statistics for public health data. Wiley, Hoboken
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Goicoa, T., Ugarte, M.D., Etxeberria, J. et al. Comparing CAR and P-spline models in spatial disease mapping. Environ Ecol Stat 19, 573–599 (2012). https://doi.org/10.1007/s10651-012-0201-8
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10651-012-0201-8