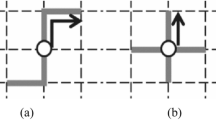
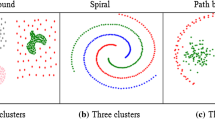
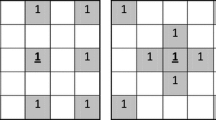
Abstract
The geographic delineation of irregularly shaped spatial clusters is an ill defined problem. Whenever the spatial scan statistic is used, some kind of penalty correction needs to be used to avoid clusters’ excessive irregularity and consequent reduction of power of detection. Geometric compactness and non-connectivity regularity functions have been recently proposed as corrections. We present a novel internal cohesion regularity function based on the graph topology to penalize the presence of weak links in candidate clusters. Weak links are defined as relatively unpopulated regions within a cluster, such that their removal disconnects it. By applying this weak link cohesion function, the most geographically meaningful clusters are sifted through the immense set of possible irregularly shaped candidate cluster solutions. A multi-objective genetic algorithm (MGA) has been proposed recently to compute the Pareto-sets of clusters solutions, employing Kulldorff’s spatial scan statistic and the geometric correction as objective functions. We propose novel MGAs to maximize the spatial scan, the cohesion function and the geometric function, or combinations of these functions. Numerical tests show that our proposed MGAs has high power to detect elongated clusters, and present good sensitivity and positive predictive value. The statistical significance of the clusters in the Pareto-set are estimated through Monte Carlo simulations. Our method distinguishes clearly those geographically inadequate clusters which are worse from both geometric and internal cohesion viewpoints. Besides, a certain degree of irregularity of shape is allowed provided that it does not impact internal cohesion. Our method has better power of detection for clusters satisfying those requirements. We propose a more robust definition of spatial cluster using these concepts.
Similar content being viewed by others
References
Abrams AM, Kulldorff M, Kleinman K (2006) Empirical/ asymptotic P-values for Monte Carlo-based hypothesis testing: an application to cluster detection using the scan statistics. Adv Dis Surveill 1: 1
Agarwal D, McGregor A, Venkatasubramanian S, Zhu Z (2006) Spatial scan statistics approximations and performance study. In: Conference on knowledge discovery in data mining
Aldstadt J, Getis A (2006) Using AMOEBA to create a spatial weights matrix and identify spatial clusters. Geogr Anal 38: 327–343
Assunção RM, Costa MA, Tavares A, Ferreira SJ (2006) Fast detection of arbitrarily shaped disease clusters. Stat Med 25: 723–742
Carrano EG, Soares LAE, Takahashi RHC, Saldanha RR (2006) Neto OM electric distribution network multiobjective design using a problem-specific genetic algorithm. IEEE Trans Power Deliv 21(2): 995–1005
Chankong V, Haimes YY (1983) Multiobjective decision making: Theory and methodology. Elsevier-North Holland
Conley J, Gahegan M, Macgill J (2005) A genetic approach to detecting clusters in point data sets. Geogr Anal 37: 286–314
Deb K, Pratap A, Agrawal S, Meyarivan T (2002) A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans Evol Comput 2(6): 182–197
Dematteï C, Molinari N, Daurès JP (2007) Arbitrarily shaped multiple spatial cluster detection for case event data. Comput Stat Data Anal 51: 3931–3945
Duczmal L, Assunção R (2004) A simulated annealing strategy for the detection of arbitrarily shaped spatial clusters. Comput Stat Data Anal 45: 269–286
Duczmal L, Buckeridge DL (2006) A workflow spatial scan statistics. Stat Med 25: 743–754
Duczmal L, Kulldorff M, Huang L (2006) Evaluation of spatial scan statistics for irregularly shaped disease clusters. J Comput Graph Stat 15: 428–442
Duczmal L, Cançado ALF, Takahashi RHC, Bessegato LF (2007) A genetic algorithm for irregularly shaped spatial scan statistics. Comput Stat Data Anal 52: 43–52
Duczmal L, Moreira GJP, Ferreira SJ, Takahashi RHC (2007) Dual graph spatial cluster detection for syndromic surveillance in networks. Adv Dis Surveill 4: 88
Duczmal L, Cançado ALF, Takahashi RHC (2008) Geographic delineation of disease clusters through multi-objective optimization. J Comput Graph Stat 17: 243–262
Duczmal L, Duarte AR, Tavares R (2009) Extensions of the scan statistics for the detection and inference of spatial clusters. In: Glaz J, Pozydnyakov V, Wallestein S (eds) Scan statistics. Birkhäuser, pp 157–182 (to appear)
Dwass M (1957) Modified randomization tests for nonparametric hypotheses. Ann Math Stat 28: 181–187
Gaudart J, Poudiougou B, Ranque S, Doumbo O (2005) Oblique decision trees for spatial pattern detection: optimal algorithm and application to malaria risk. BMC Med Res Methodol 5: 22
Iyengar VS (2004) Space-time clusters with flexible shapes. IBM Research Report RC23398(W0408-068)
Jacquez GM, Kaufmann A, Goovaerts P (2007) Boundaries, links and clusters: a new paradigm in spatial analysis? Environ Ecol Stat (Published online)
Kulldorff M, Nagarwalla N (1995) Spatial disease clusters: detection and inference. Stat Med 14: 799–810
Kulldorff M (1997) A spatial scan statistics. Commun Stat Theory Methods 26(6): 1481–1496
Kulldorff M (1999) Spatial scan statistics: models, calculations, and applications. In: Balakrishnan N, Glaz J (eds) Scan statistics and applications. Birkhäuser, Boston, pp 303–322
Kulldorff M, Tango T, Park PJ (2003) Power comparisons for disease clustering tests. Comput Stat Data Anal 42: 665–684
Kulldorff M, Huang L, Pickle L, Duczmal L (2006) An elliptic spatial scan statistics. Stat Med 25: 3929–3943
Lawson A, Biggeri A, BVohning D, Lesare E, Viel JF, Bertollini R (1999) Disease mapping and risk assessment for public health. Wiley, London
Lawson A (2001) Statistical methods in spatial epidemiology. In: Lawson A (eds) Large scale: surveillance. Wiley, New York, pp 197–206
Modarres R, Patil GP (2007) Hotspot detection with bivariate data. J Stat Plan Inference 137: 3643–3654
Moura FR, Duczmal L, Tavares R, Takahashi RHC (2007) Exploring multi-cluster structures with the multi-objective circular scan. Adv Dis Surveill 2: 48
Neill DB, Moore AW, Pereira F, Mitchell T (2005) Detecting significant multidimensional spatial clusters. Adv Neural Inf Process Syst 17: 969–976
Neill DB, Moore AW, Cooper GE (2007) A multivariate Bayesian scan statistics. Adv Dis Surveill 2: 60
Patil GP, Taillie C (2004) Upper level set scan statistics for detecting arbitrarily shaped hotspots. Environ Ecol Stat 11: 183–197
Patil GP, Modarres R, Myers WL, Patankar P (2006) Spatially constrained clustering and upper level set scan hotspot detection in surveillance geoinformatics. Environ Ecol Stat 13: 365–377
Sahajpal R, Ramaraju GV, Bhatt V (2004) Applying niching genetic algorithms for multiple cluster discovery in spatial analysis. In: International conference on intelligent sensing and information processing
Takahashi RHC, Vasconcelos JA, Ramirez JA, Krahenbuhl L (2003) A multiobjective methodology for evaluating genetic operators. IEEE Trans Magnetics 39(3): 1321–1324
Tango T, Takahashi K (2005) A flexibly shaped spatial scan statistics for detecting clusters. Int J Health Geogr 4: 11
Yiannakoulias N, Rosychuk RJ, Hodgson J (2007) Adaptations for finding irregularly shaped disease clusters. Int J Health Geogr 6(1): 28
Yiannakoulias N, Karosas A, Schopflocher DP, Svenson LW, Hodgson MJ (2007) Using quad trees to generate grid points for application in geographic disease surveillance. Adv Dis Surveill 3
Wieland SC, Brownstein JS, Berger B, Mandl KD (2007) Density-equalizing Euclidean minimum spanning trees for the detection of all disease cluster shapes. PNAS 104(22): 904–909
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Duarte, A.R., Duczmal, L., Ferreira, S.J. et al. Internal cohesion and geometric shape of spatial clusters. Environ Ecol Stat 17, 203–229 (2010). https://doi.org/10.1007/s10651-010-0139-7
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10651-010-0139-7