1 Introduction

In re mathematica ars proponendi quaestionem pluris facienda est quam solvendi. (Cantor, 1867, p. 26)

Transl.: In mathematics, the art of posing a question is of greater value than solving it.

In his statement, Cantor emphasizes the importance of the ability to pose substantial questions within mathematics. In fact, problem posing is considered a central activity of mathematics (Hadamard, 1945; Halmos, 1980), and at the latest since the 1980s (Brown & Walter, 1983; Butts, 1980; Kilpatrick, 1987), it is being investigated with growing interest by mathematics education researchers. Since the 1990s, it has been widely used to identify or assess mathematical creativity and abilities (Silver, 1994, 1997; Singer & Voica, 2015; Van Harpen & Sriraman, 2013; Yuan & Sriraman, 2011). Silver (1997, p. 76) emphasizes that to grasp such constructs, both products and processes of problem-posing activities can be considered. However, a strong product orientation within research on problem posing is noticeable (Bonotto, 2013; Singer et al., 2017; Van Harpen & Sriraman, 2013); that is, studies aiming to assess mathematical creativity, for example, often focus on the posed problems rather than the processes that led to them. This is noteworthy, since processes are central to educational research. As Freudenthal (1991) states:

[T]he use of and the emphasis on processes is a didactical principle. Indeed, didactics itself is concerned with processes. Most educational research, however, and almost all of it that is based on or related to empirical evidence, focuses on states (or time sequences of states when education is to be viewed as development). States are products of previous processes. As a matter of fact, products of learning are more easily accessible to observation and analysis than are learning processes which, on the one hand, explains why researchers prefer to deal with states (or sequences of states), and on the other hand why much of this educational research is didactically pointless. (p. 87, emphases in original)

Although there are studies considering problem-posing processes (Headrick et al., 2020; Ponte & Henriques, 2013), general knowledge about learners’ problem-posing processes remains limited (Cai & Leikin, 2020). Only a few studies are dedicated to the development of a phase model for problem posing (Cruz, 2006; Pelczer & Gamboa, 2009). Those models still hold the potential for sufficient generalization and validation. This knowledge could help to develop a more sophisticated process-oriented perspective on problem posing. The few studies that examine the general process of problem posing (Koichu & Kontorovich, 2013; Patáková, 2014; Pelczer & Rodríguez, 2011) may benefit from a validated phase model. Such a model may also be useful for the effective educational use of problem posing in the classroom. This study aims to develop a valid and reliable category system that allows analyzing problem-posing processes. These kinds of conceptual frameworks play a central role in mathematics education research as they enable a better understanding of thinking processes (Lester, 2005; Schoenfeld, 2000).

2 Theoretical background

2.1 Problem posing

There are two widespread definitions of problem posing which are used or referred to in most studies on the topic. As a first definition, Silver (1994, p. 19) describes problem posing as the generation of new problems and reformulation of given problems. Silver continues that both activities can occur before, during, or after a problem-solving process. As a second definition, Stoyanova and Ellerton (1996, p. 218) refer to problem posing as the “process by which, on the basis of mathematical experience, students construct personal interpretations of concrete situations and formulate them as meaningful mathematical problems.” In the following, we adopt the definition of Silver (1994) as the differentiation between the activities of generation and reformulation is beneficial for identifying different activities in problem-posing processes. However, both definitions are not disjunctive or contradictory but describe equivalent activities.

In both definitions, the term problem is used for any kind of mathematical task, whether it is a routine or a non-routine problem (Pólya, 1966). For the former, “one has ready access to a solution schema” (Schoenfeld, 1985b, p. 74), and for the latter, one has no access to a solution schema. Thus, problem posing can lead to any kind of task on the spectrum between routine and non-routine problems (Baumanns & Rott, 2019; Baumanns & Rott, 2021a).

Stoyanova and Ellerton (1996) distinguish between free, semi-structured, and structured problem-posing situations depending on the degree of structure. A situation is an ill-structured problem in the sense that its goal cannot be determined by all given elements and relationships (Stoyanova, 1997). Because this study focuses on structured situations and Baumanns and Rott (2021a) encountered difficulties in distinguishing free and semi-structured situations, in this article, we distinguish between unstructured and structured situations. Unstructured situations form a spectrum of situations without an initial problem. The given information of these situations reaches from nearly none (see Table 1, situation 1) to open situations with numerous given information, the structure of which must be explored by using mathematical knowledge and mathematical concepts (see Table 1, situation 2). In structured situations, people are asked to pose further problems based on a specific problem, for example, by varying its conditions (see Table 1, situation 3). The phase model developed in this article aims to describe problem-posing activities that are induced by situations like those in Table 1. In particular, the model is developed using structured situations.

Table 1 Unstructured and structured problem-posing situations
Full size table

2.2 Process of problem posing—state of research

Because products may be more accessible by analysis than processes (Freudenthal, 1991), most problem-posing studies focus on posed problems (Bicer et al., 2020; Van Harpen & Presmeg, 2013; Yuan & Sriraman, 2011). However, consideration of the processes increases in recent studies (Cai & Leikin, 2020; Crespo & Harper, 2020; Headrick et al., 2020; Koichu & Kontorovich, 2013; Patáková, 2014; Pelczer & Rodríguez, 2011). Ponte and Henriques (2013), for example, examine the problem-posing process in investigation tasks among university students and found that problem posing and problem-solving complement each other in generalizing or specifying conjectures to obtain more general knowledge about the mathematics contents. Christou et al. (2005) describe four thinking processes that occur within problem posing, namely editing, selecting, comprehending/organizing, and translating quantitative information. They found the most able students are characterized through editing and selecting processes. However, compared to the present study, these activities do not tend to describe problem-posing processes by phases. Instead, Christou et al. (2005) intend to characterize thinking processes in problem posing. Cifarelli and Cai (2005) include problem posing in their model to describe the structure of mathematical exploration in open-ended problem situations. They identify a recursive process in which reflection on a problem’s solutions serves as the source of new problems.

The studies cited above differ from the present study as follows: They describe and analyze only individual processes, they describe the problem-posing process in terms of thinking processes rather than phases, or they consider problem-posing processes as a sub-phase of a superordinate process. However, there is a lack of studies that attempt to derive a general, descriptive phase model of observed problem-posing processes themselves from numerous processes. For problem-solving research, the analysis of processes through phase models has been established at least since Pólya’s (1945) and Schoenfeld’s (1985b) seminal works. While their models are normative, which means they function as advice on how to solve problems, newer empirical studies on the process of problem-solving develop and investigate descriptive models, which means they portray how problems are actually solved by participants (Artzt & Armour-Thomas, 1992; Rott et al., 2021; Yimer & Ellerton, 2009). This study also focuses on descriptive models.

Some researchers interpret problem posing as a problem-solving activity (Arıkan & Ünal, 2015; Kontorovich et al., 2012; Silver, 1995), and there are several established models of problem-solving processes (e.g., Mason et al., 1982; Pólya, 1945). Therefore, it is a reasonable question whether a separate phase model for problem posing is needed. From the observations of problem-solving and problem-posing activities within the present study, we share the argument by Pelczer and Gamboa (2009) that the cognitive processes involved in problem posing are of their own nature and cannot be adequately described by the phase models of problem solving. For problem posing, Cai et al. (2015) state, “there is not yet a general problem-posing analogue to well-established general frameworks for problem solving such as Polya’s (1957) four steps” (p. 14).

To find existing research on this topic, we conducted a systematic literature review (Baumanns & Rott, 2021a, 2021b). This review encompassed articles from high-ranked journals of mathematics education, the Web of Science, PME proceedings, the 2013 and 2020 special issues in Educational Studies of Mathematics, the 2020 special issue in International Journal of Educational Research, and two edited books on problem posing (Felmer et al., 2016; Singer et al., 2015). From all reviewed articles, three were dedicated to the development of general phases in problem posing similarly to the present study.

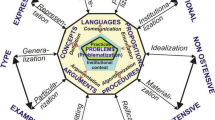
Cruz (2006) postulates a phase model based on a training program for teachers (see Fig. 1). For this reason, this phase model is preceded by educative needs and goals. Once a concrete teaching goal has been set (1), the episode type of problem formulating begins (2). This episode has a problem as its output which is then solved (3). If it cannot be solved, the problem may have to be reformulated (4). A solvable problem is further developed in the episode type problem improving (5). The complexity of the problem is adapted to the learning group and compared with the goal (6 and 7). If the comparison shows that the problem is not suitable, either further changes are made to the task (8) or the task is rejected as unsuitable.

Fig. 1
figure 1

Phase model of problem posing by Cruz (2006)

Full size image

Pelczer and Gamboa (2009) distinguish five phases—setup, transformation, formulation, evaluation, and final assessment—based on the analysis of problem-posing processes in unstructured situations. The setup includes the definition of the mathematical context of a situation and the reflection on the knowledge needed to understand the situation. This assessment serves as a starting point for the subsequent process. During the transformation, the conditions of a problem are analyzed, and possibilities for modification are identified, reflected, and executed. In the formulation, all activities related to the formulation of a task are summarized. This includes the consideration of different possible formulations of the problem as well as an evaluation of these formulations. In the evaluation, a posed problem is assessed in terms of various aspects, for example, whether it fulfills the initial conditions or further modifications are needed. In the final assessment, the process of posing a problem is reflected upon, and the problem itself is evaluated, for example, in terms of difficulty and interest. In their study, Pelczer and Gamboa (2009) compare experts’ and novices’ problem-posing processes, identifying different trajectories, that is, transitions between the stages. While experts more often go through recursive processes, processes of novices are more linear and often occur without transformation and final assessment.

Koichu and Kontorovich (2013) developed four stages, observed in the context of two successful problem-posing activities: (1) In the warming-up phase, typical problems spontaneously associated with the given situation are posed that serve as a starting point. (2) In the phase searching for an interesting mathematical phenomenon, participants concentrate on selected aspects of the given task to identify interesting aspects that can be used for forthcoming problems. (3) Since the intention is to develop interesting problem formulations, in the phase hiding the problem-posing process in the problem formulation, the posers try to disguise to the potential solvers in which way the task was created. (4) Finally, in the reviewing phase, the posers evaluate the problems based on individual criteria such as the degree of difficulty or appropriateness for a specific target group.

In general, Cruz’ (2006) phase model does not allow for sufficient generalization to processes of sample groups that do not pursue school learning goals such as students or mathematicians. The model by Pelczer and Gamboa (2009) has the potential to verify the validity by checking objective coding. The stages by Koichu and Kontorovich (2013) are developed on a small sample of two people and therefore need to be tested for applicability to larger sample groups. All these potentials will be addressed in this article. In addition, although the models presented have certain similarities, they also show numerous characteristic differences. In comparison, phase models for problem-solving (Artzt & Armour-Thomas, 1992; Pólya, 1945; Rott et al., 2021; Schoenfeld, 1985b; Yimer & Ellerton, 2009) share a very similar core structure. Thus, there is a conceptual and empirical need for a generally applicable model for problem-posing research.

The need for developing a phase model for problem posing is, furthermore, based on our general observation that the quality of the posed problems did not always match the quality of the observed activity. In our opinion, it is therefore not enough to consider only the products when, for example, problem posing is used to assess mathematical creativity. Furthermore, developing a process-oriented framework serves as research for discussing and analyzing these processes (Fernandez et al., 1994, p. 196).

2.3 Research questions

The research goal of this study is to develop a descriptive phase model for problem-posing activities based on structured situations. The lack of phase models constitutes a desideratum from which the following research questions emerge:

  1. (1)

    Which recurring and distinguishable activities can be identified when dealing with structured problem-posing situations?

  2. (2)

    What is the general structure (i.e., sequence of distinguishable activities) of the observed processes from which a descriptive phase model may be derived?

The goal of these research questions is to develop a descriptive phase model that allows analyzing problem-posing processes. To evaluate the quality of this model, we draw on the criteria by Schoenfeld (2000) that can be used for evaluating models in mathematics education. As this type of coding is highly inferential (Rott et al., 2021; Schoenfeld, 1985b), special emphasis is given to interrater agreement.

3 The study

3.1 Data collection

The present study is a generative study that aims to “generate new observation categories and new elements of a theoretical model in the form of descriptions of mental structures or processes that explain the data” (Clement, 2000, p. 557). For such studies, a less structured, qualitative approach is appropriate that is open to unexpected findings (Döring & Bortz, 2016, p. 192), such as task-based interviews. Task-based interviews have particularly been used in problem-solving research to gain insights into the cognitive processes of participants (Konrad, 2010, p. 482). The interviews were conducted in pairs to create a more natural communication situation and eliminate the constructed pressure to produce something mathematical for the researcher (Schoenfeld, 1985a, p. 178). Johnson and Johnson (1999) also underline that cooperative learning groups such as pairs are “windows into students’ minds” (p. 213). For this reason, the interviewer avoided intervening in the interaction process.

The interviews were conducted with 64 pre-service primary and secondary mathematics teachers (PST). The PSTs worked in pairs on one of two structured problem-posing situations, either (A) Nim game or (B) Number pyramid, which are presented in Table 2. The participants were informed that both problem solving and problem posing were central. After the initial problem solving, both situations stated: “Based on this task, pose as many mathematical tasks as possible.” This open and restriction-free question should stimulate a creative process. A common question of understanding from participants was, using the example of situation (A), whether they should now pose further Nim games or were also allowed to depart from them. This decision was left to the PSTs’ creativity.

Table 2 Structured problem-posing situations used in this study
Full size table

In total, 15 processes of situation (A) and 17 processes of situation (B), ranging from 9 to 25 min, have been recorded and analyzed. The processes ended when no ideas for further problems emerged from the participants. In total, 7 h and 46 min of video material were recorded and analyzed. Thus, the processes had an average length of 14.5 min. Four pairs of PSTs each were in the same room under authentic university seminar conditions. A camera was positioned opposite the pairs capturing all the participants’ actions. To accustom them to natural communication in front of the camera, short puzzles were performed before problem posing.

3.2 Data analysis

For data analysis, we adapted Schoenfeld’s (1985b) verbal protocol analysis, originally used to analyze problem-solving processes. This method is an event-based sampling. Compared to time-based sampling, the processes are not divided into fixed time segments (e.g., 30 s), which are then coded. Instead, new codes are set when the participants’ behavior changes. This method has two steps: At first, the recorded interviews are segmented into “macroscopic chunks of consistent behavior” (Schoenfeld, 1985b, p. 292) that are called episodes in which “an individual or a problem-solving group is engaged in one large task [...] or closely related body of tasks in the service of the same goal” (Schoenfeld, 1985b, p. 292). In a second step, the episodes are then characterized in terms of content.

To answer the first research question, verbal protocol analyses were employed in terms of inductive category development (Mayring, 2014, pp. 79–87), meaning that the episode types were developed data-derived. The descriptions of the episode types were additionally concretized in a theory-based manner. For that, the above-mentioned conceptual and empirical findings of problem-posing research (Cruz, 2006; Pelczer & Gamboa, 2009; Silver, 1994), as well as findings of research on phase models in problem solving (Pólya, 1945; Schoenfeld, 1985b), were used. This procedure aims to develop exclusive and exhaustive codes (Cohen, 1960), that is, episode types, that can be assigned to the observed problem-posing processes.

To answer the second research question, recurring sequences of the episode types were identified to develop a general phase model. Both general sequences in the observed processes, as well as conceptual insights about problem-posing activities in general, were considered. To analyze the interrater agreement, an independent second coder was trained. At first, the second coder was given the coding manual and a process to code without further comment. For this first coding, cases of doubt were discussed within 2 h of training. After this training, the second coder analyzed about 2 h and 23 min of the total video material of 7 h and 46 min which means 10 randomly chosen processes out of 32. Thus, the second coder analyzed about 30.7% of the total video material. Finally, cases of doubt of coding were discussed via consensual validation. These codings were used to calculate the interrater agreement to the author’s coding.

The interrater agreement was calculated with the EasyDIAg algorithm by Holle and Rein (2015). EasyDIAg provides an algorithm that converts two codes of an event-based sampling data set into an agreement table from which Cohen’s kappa (Cohen, 1960) is calculated through an iterative proportional fitting algorithm. Furthermore, in contrast to the classical Cohen’s kappa, EasyDIAg provides an interrater agreement score for each value of a category. EasyDIAg considers raters’ agreement on segmentation and categorization as well as the temporal overlap of the raters’ annotations. This makes this algorithm particularly suitable for assessing the interrater agreement of the event-based sampling data set at hand. For the agreement, we used an overlap criterion of 60% as suggested by Holle and Rein (2015). In the online supplement, we provide an example analysis of a process that was coded by the authors and the second rater followed by the calculation of the interrater agreement in this manner.

4 Results

First, to retrace the inductive-deductive category development, the problem-posing process of the Nim game by Theresa and Ugur will be described in order to refer back to it when describing the developed episode types. The individual episodes are described without labelling them. The given periods indicate the minutes and seconds (mm:ss) of the respective episodes. The recorded time starts with the first attempt at posing problems after the initial problem has been solved. Compared to other participants, Theresa and Ugur get the solution of the Nim game quickly and without assistance.

Episode 1 (00:00–00:49): Theresa and Ugur first read the task that should initiate the problem posing. Ugur considers whether new tasks should now be posed in relation to the solution strategy of working backwards. Theresa considers whether the stones should be the focus of new tasks. Afterward, both reflect again on their solution strategy and consider to what extent they can use it for new tasks.

Episode 2 (00:49–02:14): Then other games like Connect Four or Tic-tac-toe, which may have a winning strategy similar to the Nim game, are collected.

Episode 3 (02:14–05:50): Both participants want to figure out whether there is a winning strategy for Tic-tac-toe. After about 3 min, they assume that an optimal game always results in a draw. They return to the Nim game and ponder whether player B also has a chance to win safely. They conclude that player B can only win if player A does not make the first move according to the winning strategy.

Episode 4 (05:50–07:43): They pose the task of how many stones are necessary for player B to win safely. Afterward, the text of the task is formulated. They also ask how many moves player A needs in order to win.

Episode 5 (07:43–09:03): The last-mentioned question of episode 4 is solved and also generalized. Ugur says, you find the number of moves of player A by going from the number of stones to the next higher number divisible by three, and then dividing this number by three.

Episode 6 (09:03–09:44): Ugur suggests increasing the number of stones that can be removed from the table. Specifically, he suggests that one to three stones can be removed. Meanwhile, Theresa writes down these ideas.

Episode 7 (09:44–10:32): Theresa writes down the previously posed problems without working on the content of the formulations.

Episode 8 (10:32–13:48): Both play the variation of the Nim game raised in episode 6. They express that they want to develop a winning strategy for this variation. They quickly realize that player B can safely win the game since multiples of four are now winning numbers and the 20 stones that are on the table at the beginning are already divisible by four. They validate this strategy afterward. At the last minute, the newly posed variation is also evaluated as exciting.

Episode 9 (13:48–14:13): Ugur wants to generalize the game further and poses the task of how to win when the players can remove one to n stones. Theresa asks Ugur if his goal is a general formula.

Episode 10 (14:13–15:48): This task is then solved by Ugur by transferring the structure of the solution of the initial problem to the generalization. Ugur formulates that if you are allowed to remove one to n − 1 stones, the player who has the turn must bring the number of stones to n by his turn to win safely.

Episode 11 (15:48–16:42): Subsequently, both work on a suitable formulation for this generalized task.

Episode 12 (16:42–18:28): Theresa notes that solving the initial problem is challenging and therefore suggests providing help for pupils. Theresa suggests that it might help when the pupils first develop a winning strategy for the simple case that the players can only remove one stone. Ugur suggests further help cards which can be requested by the pupils themselves if they get stuck.

Episode 13 (18:28–19:50): Theresa wants to focus on new tasks again. They move away from the initial problem and use the stones to create an iconic representation of the triangular numbers (1, 3, 6, ...). They formulate the task to find a general formula to calculate the n-th triangular number.

Episode 14 (19:50–21:33): Theresa puts the stones in rows of three so that the structure that leads to the winning strategy is more visible. She evaluates this presentation by emphasizing the usefulness of this method for extensions of the Nim game with more than 20 stones on the table. The process comes to an end as Theresa and Ugur, when asked by the interviewer, agree not to generate any more ideas.

4.1 Category development of episode types in problem posing

Using the described evaluation method, five episode categories were developed which allow the observed processes to be described in a time-covering manner. These episode categories are situation analysis, variation, generation, problem-solving, and evaluation. In the following, the developed categories of episode types are described. The episodes of the process by Theresa and Ugur (T&U) described above are assigned to these episode types for a better comprehension of the episode types. In addition, we provide further anchor examples in the online supplement. Subsequently, indications are given for coding the individual categories. Finally, the categories are discussed regarding the state of research.

4.1.1 Situation analysis

Description

During the situation analysis, the posers capture single or multiple conditions of the initial task. They usually recognize which conditions are suitable and to what extent, to create a new task by variation (changing or omitting single or multiple conditions) or generation (constructing single or multiple new conditions). In addition, the subsequent investigation of the initial task’s solution is summarized in this episode. This also includes the creation of clues or supporting tasks that lead to the solution of the initial task.

In the process of T&U, episode 1 is coded as situation analysis as the participants still reflect on their solution strategy. Also, episode 12 is coded as situation analysis because both PSTs try to come up with ideas on how to support students with solving the initial problem. A further example of other participants who capture the conditions of the initial problem can be found in the online supplement.

Coding instructions

It is not always clear when the posers are engaged in reading (see non-content-related episodes below) or have already moved on to situation analysis. Simultaneous coding is possible here. The creation of supporting tasks, which are supposed to assist in solving the initial problem, is interpreted as an analytical examination of the situation and is therefore coded as situation analysis.

4.1.2 Variation

Description

During variation, single or multiple conditions of the initial task or a task previously posed in the process are changed or omitted. No additional conditions are constructed. In addition, writing down and formulating the respective task is included under this episode.

In the process of T&U, episodes 4, 6, 9, and 11 are coded as variation. In episode 6, for example, Ugur varies one specific rule of the Nim game and states that the players are now allowed to remove one to three stones from the table. In episode 9, this is further generalized by variation.

Coding instructions

For the identification of variation, the What-If-Not-strategy by Brown and Walter (2005) should be used. The first step of this strategy is intended to extract the conditions of a problem. The Nim game, for example, has at least the following five conditions: (1) 20 stones, (2) two players, (3) alternating moves, (4) one or two stones are removed, and (5) whoever empties the table wins. This analysis should be done before coding. Omitting or varying these analyzed conditions will be coded as variation. Also, omitting or varying conditions of a previously posed problem is coded as variation.

4.1.3 Generation

Description

During generation, tasks are raised by constructing new conditions to the given initial task or a task previously posed in the process. Due to the possible change in the task structure, posers sometimes explain the new task. In addition, writing down and formulating the respective task is summarized under this episode type. Also, free associations, in which tasks similar to the initial task are reminded, are coded as generation.

In the process of T&U, episodes 2 and 13 are coded as generation. In episode 13, for example, they move further away from the Nim game and use the stones to ask questions about dot patterns.

Coding instructions

The episode types variation and generation are not always clearly distinguishable from each other. Although the coding focuses on the activity of the poser and not on the emerged task, it can help to examine the characteristics of a task resulting from variation or generation. In the case of a varied task, the question or the solution structure often remains unchanged. In the case of a generated task, there is usually a fundamentally different task whose solution often requires different strategies.

4.1.4 Problem solving

Description

Problem solving describes the activity in which the posers solve a task that they have previously posed. If a non-routine problem has been posed, the respondents go through a shortened problem-solving process in which the phases of devising and carrying out the plan (Pólya, 1945) are the main focus. In some cases, the posers omit to carry out the plan if the plan already provides sufficient information on the solvability and complexity of the posed problem. If a routine problem has been posed, the solution is usually not explained, since the method of solution is known. However, longer phases of solving routine tasks are also coded as problem solving.

In the process of T&U, episodes 3, 5, 8, and 10 are coded as problem solving as the participants are engaged in solving their posed problems.

Coding instructions

Although solving a routine problem should be differentiated from solving a non-routine problem, both activities are labelled with the same code. However, the commentary of the coding should specify whether an episode is an activity of solving a routine or a non-routine problem.

4.1.5 Evaluation

Description

In the evaluation, the posers assess the posed tasks based on individually defined criteria. In the processes observed, posers asked whether the posed problem is solvable, well-defined, similar to the initial task, appropriate for a specific target group, or interesting for themselves to solve. On the basis of this evaluation, the posed task is then accepted or rejected.

In the process of T&U, episode 14 is coded as evaluation, and in episode 8, there is a simultaneous coding of problem-solving and evaluation. In episode 8, for example, the participants are initially engaged in problem-solving. Towards the end of this episode, they both assess their posed problem based on their interest in solving it.

Coding instructions

Often, evaluative statements are made about the course of an episode of problem-solving, since the criteria for the evaluation of a posed problem (e.g., solvability or interest) are based on sufficient knowledge about the solution of the posed problem. In such cases, the episode types of problem-solving and evaluation cannot be separated empirically, which is why simultaneous coding is permitted. The criterion for this simultaneous coding is that during an episode of problem-solving, an evaluative statement must come within a 30-s window for a simultaneous coding to be made. For example, if at least one evaluative statement falls during the first 30 s of a problem-solving episode, both types of episodes are coded simultaneously. If at least one evaluative statement also falls within the following 30 s of problem-solving, both episode types are again encoded simultaneously.

4.1.6 Non-content-related episode types

When participants, for example, ran out of ideas or became distracted during the interview, they engage in the following non-content-related activities. Such activities were also identified in descriptive models of problem solving (Rott et al., 2021). In the process of T&U, episode 7 was coded as non-content-related episode.

Reading

The episode of reading consists of reading the situation text as well as a shorter exchange about what has been read to make sure that the text is understood. Since the participants have usually already solved the initial task of the situation, the reading takes place rather in between.

Writing

In the episode of writing, posers write down the text of a problem they have already worked out orally. Also, the posers write down the solution of a previously posed problem. Writing is only coded if no solution or problem formulation is being worked on in terms of content (e.g., specify the problem text).

Organization

Organization includes all activities in which the poser is working on the situation, but where no content-related work is apparent. This includes, for example, the lengthy production of drawings.

Digression

The episode digression is encoded when the posers are not engaged with the situation. This may include informal conversations with the other person about topics that are not related to the task (e.g., weekend activities) or looking out of the window for a long time.

Other

All episodes that cannot be assigned to any other episode type are coded as other.

4.1.7 Discussion

To provide a theoretical justification of the data-driven episode types of problem posing, we want to connect the five episode types with the presented state of research on problem-posing phase models.

Situation analysis

In Pelczer’s and Gamboa’s (2009) phase model, we find aspects of situation analysis in their transformation stage. One sub-process of this transformation stage is the analysis of the problem’s characteristics. Terminologically, the episode name is based on Schoenfeld’s (1985a, 1985b) analysis, because we observed that, similar to problem-solving, posers identify what possibilities for problem posing the given situations provide through their conditions.

Variation

Pelczer and Gamboa (2009) have aspects of variation in the stage of formulation in which a problem is written down and the formulation is evaluated. Problem formulating can also be found in the model by Cruz (2006). The principle of variation also plays a central role in problem solving. Schoenfeld (1985b), for example, suggests posing modified problems by replacing or varying the conditions of a particular problem that is difficult to solve.

Generation

Koichu and Kontorovich (2013) consider spontaneously associated problems related to a given problem-posing situation in their model, yet this is only one aspect of the generation described above. The distinction between variation and generation is theoretically already conceptualized by Silver (1994). In empirical studies on problem posing, there are so far no objective criteria that enable distinct identification of both activities. The phase model at hand proposes criteria for this distinction.

Problem-solving

Cruz (2006) explicitly mentions problem solving as a stage in his problem-posing phase model. In the model by Pelczer and Gamboa (2009), problem solving is implicit in the evaluation phase, in which the posed problem is assessed and modified. This is presumably done based on the solution of it.

Evaluation

The stage of evaluation in the phase model by Pelczer and Gamboa (2009) shares the same name and has similar characteristics. Cruz (2006) implicitly considers evaluation when the posers improve the posed problem when they deem it not suitable for a specific learning group. The activity of evaluation is closely related to the metacognitive activity of the regulation of cognition (Flavell, 1979; Schraw & Moshman, 1995). In research on problem posing, there are hardly any studies that investigate metacognitive behavior, yet some frameworks implicitly include aspects of it. Kontorovich et al. (2012), for example, consider aptness by means of fitness, suitableness, and appropriateness of a posed problem.

4.2 Derivation of a descriptive phase model for problem posing

There is no predetermined order of episode types which means there can be transitions from any episode type to any other. However, there is a kind of “natural order” in which episode types appear in most processes and in which transitions often occur. This has been indicated by the order in which the episode types were presented in Sect. 4.1. It was observed that first the conditions of a situation are grasped (situation analysis) and then new tasks are posed through variation or generation; these tasks are solved in order to evaluate them based on the solution. Of course, we did not observe exactly this order in every process, but across the participants and the different problem-posing situations, parts of this superordinate pattern were identified. Often the situation analysis was observed at the beginning of the process and at the end of a longer phase of variation. Also typical were frequent changes between variation or generation and problem solving (sometimes in combination with evaluation). Furthermore, problem posing was identified as a cyclical activity. Several participants were observed to revise or to further vary their previously posed problems. Figure 2 shows the T&U’S process following Schoenfeld’s (1985b) illustrations of problem-solving processes. Several characteristic transitions can be observed in this process. The vertical lines shown in this figure indicate points in time when a new task (either by variation or by generation) was posed.

Fig. 2
figure 2

Example of a timeline chart of the problem-posing process by Theresa and Ugur as described in Sect. 4 following the illustrations by Schoenfeld (1985b)

Full size image

From these theoretically justifiable as well as empirically observable patterns in the sequence of episodes, the descriptive phase model shown in Fig. 3 was derived. It contains all five content-related episodes as a complete graph. All transitions indicated by arrows can occur and have been observed empirically in the study. However, not all episode types need to occur in a process. Several participants were observed to revise or to further vary their previously posed problems. In addition, in most cases, not only one but several problems are posed in numerous cycles. The model reflects this observation through its cyclic structure. The model is used to represent all these possible paths within the problem-posing process.

Fig. 3
figure 3

Descriptive phase model for problem posing based on structured situations

Full size image

To check the interrater agreement, 30.7% of the total video material of 7 h and 46 min was coded by a second independent rater and combined into an agreement table (see Table 3) using the EasyDIAg algorithm (Holle & Rein, 2015). As explained in Sect. 4.1.5, the episode types of problem solving and evaluation have empirically often been observed simultaneously, which is why simultaneous coding was allowed. We have, therefore, considered this simultaneous coding as a separate category for the verification of interrater agreement. If the start or end of a process was coded differently in time by the two raters, there are unlinked events in the agreement which are coded as X. The entry X–X in Table 3 can, therefore, not occur empirically.

Table 3 Agreement table for all seven categories of episodes as determined by EasyDIAg. The %overlap parameter was set to 60%. Abbreviations: SA situation analysis, V variation, G generation, PS problem-solving, PS/E problem solving and evaluation (simultaneous coding), E evaluation, O others, X no match)
Full size table

With a Cohen’s kappa of κ = 0.81, the interrater agreement is almost perfect (Landis & Koch, 1977, p. 165). This high level of agreement is particularly gratifying as the evaluation method is a highly subjective and interpretative procedure, yet the developed categories are capable of consistent coding. As anticipated, the biggest coding differences are observed for the categories variation and generation as well as the distinction between the categories of problem solving, problem solving and evaluation, and evaluation. The kappa calculated for the separate categories are (with the abbreviations from Table 3 as indices) κSA = 0.87, κV = 0.83, κG = 0.72, κPS = 0.87, κPS/E = 0.73, κE = 0.49, and κO = 97.

5 Discussion

This study aimed to develop a valid and reliable model to describe and analyze problem-posing processes. Schoenfeld (2000) provides eight criteria for evaluating models in mathematics education: (i) descriptive power, (ii) explanatory power, (iii) scope, (iv) predictive power, (v) rigor and specificity, (vi) falsifiability, (vii) replicability, and (viii) multiple sources of evidence. Criteria (i), (iii), (v), and (vii) will be outlined to discuss the potential and limitations of the presented framework.

Regarding research question (1), five content-related episode types—situation analysis, variation, generation, problem solving, and evaluation—were identified inductively which enable objective coding through their operationalization. The episode types of the developed phase model enable a specific descriptive perspective on all observed problem-posing processes in the study in a time-covering manner. This description, we argue, provides a better understanding of problem-posing processes in general (i). Furthermore and with regard to research question (2), from the observed processes, a general structure in terms of the sequence of the episodes was identified from which we were able to derive a descriptive process model for problem posing. The high interrater agreement attests to the replicability of the model (vii). The participants of the study were heterogeneous and ranged from PSTs in the first bachelor’s semester for primary school to PSTs in the 3rd master’s semester for high school. Equally heterogeneous were the processes that could nevertheless be analyzed by the developed model (iii). The detailed descriptions, coding instructions, and theoretical classifications provide specificity to the terms. In the online supplement, anchor examples serve for additional specification (v).

The model developed here provides additional insights compared to existing models (e.g., Cruz, 2006; Pelczer & Gamboa, 2009): It distinguishes the episode types variation and generation empirically which Silver (1994) already conceptualized theoretically. Additionally, the model encompasses non-content-related episodes for the description that have also been identified in descriptive models of problem-solving (Rott et al., 2021).

The phase model can now be used to characterize, for example, different degrees of quality of the problem-posing process which is still a recent topic in problem-posing research and for which considering the products and processes seems advisable (Kontorovich & Koichu, 2016; Patáková, 2014; Rosli et al., 2013; Singer & Voica, 2017). Thus, as in problem-solving research (cf. Schoenfeld, 1985b), a comparison between experts and novices might be a fruitful approach to identify different types of problem posers. Furthermore and following the process-oriented research on problem-solving (Rott et al., 2021), it would be conceivable that the process of posing routine tasks proceeds differently than the process of posing non-routine problems.

Finally, possible limitations to the generalizability of the developed model will be addressed. In general, the model offers one possible perspective on problem-posing processes. Depending on the selected problem-posing situation, sample, or study design, it cannot be ruled out that slightly different or even additional episode types may also occur. We also find other perspectives on problem-posing processes in research (e.g., Headrick et al., 2020). This study considers two specific structured situations with a non-routine initial problem. However, the developed phase model has also been successfully applied to situations with routine initial problems and other mathematical contents within bachelor and master theses. With small changes, the model was also successfully applied to processes based on unstructured situations in several master theses. Moreover, this study has PSTs as a sample. The phase model was successfully applied in bachelor and master theses to other sample groups such as school students and teachers (iii). Therefore, there are strong indications that support the generalizability of the phase model, which could still be clarified in follow-up studies.