Abstract
This paper develops a model with overlapping generations of households, productive public and private capital, and a golden rule of fiscal policy aimed at maximizing economic growth. Studying the transitional dynamics between steady states triggered by different exogenous shocks, we find that a waning fertility rate, coming through a weaker preference for having children, increased longevity, a decrease in subjective discounting or lower financial support for child rearing, will require a policy intervention to ensure convergence to the growth maximizing debt level. A simple calibration exercise shows that when faced with projected demographic aging the adjustments in public debt and public investment required for keeping the economy at its maximum steady state growth rate may be small.


Similar content being viewed by others
Notes
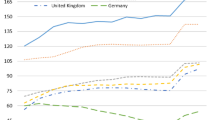
The rationale for this type of fiscal rule can be found in Blanchard and Givazzi (2002), Fatas et al. (2003). It is (or has been) practiced in Germany and the UK, among other developed economies.
For further details on the individual firms’ production function we refer to Bokan et al. (2016).
This could range from healthcare costs to education and even applied to paid parental leave.
The child rearing subsidy reduces the out-of-pocket costs of having children, though they get taxed to finance that transfer in the same degree. The subsidy is still effective, since each individual does not internalize the fertility choices of the rest of the population.
Bokan et al. (2016) finds this growth maximizing ratio in the same modelling framework used in this paper.
At steady state the model is consistent with the Kaldor (1957) facts on ratios associated with balanced growth models; we find that while the interest rate remains stable between periods labour productivity grows at a sustained rate, equal to GDP per capita growth.
The case where \(\dot{{G}_{t}}\to 0\) represents a trivial situation where all economic activity ceases to exist, since the labour augmenting productivity factor, \({h}_{t},\) goes to zero.. This case in the text above is only used to show characteristics of the motion Eq. (16) at its extreme.
Note that these steady states must be the ones associated with a below-maximum policy function between the value \(0<\dot{{G}_{t}}<{\gamma }^{A}\left({X}^{*}\right)\).
References
Aiyagari, S. R., & McGrattan, E. R. (1998). The optimum quantity of debt. Journal of Monetary Economics, 42, 447–469.
Arrow, K. (1962). The economic implications of learning by doing. Review of Economic Studies, 29, 155–173.
Aschauer, D. A. (2000). Do states optimise? Public capital and economic growth. Annals of Regional Science, 34, 343–363.
Balbo, N., Billari, F., & Mills, M. (2013). Fertility in advanced societies: A review of research / La fécondité dans les sociétés avancées: Un examen des recherches. European Journal of Population / Revue Européenne De Démographie, 29(1), 1–38.
Blanchard, O. (1985). Debt, deficits, and finite horizons. Journal of Political Economy, 93, 223–247.
Blanchard, O., & Giavazzi, F. (2002). Reforms that can be done: Improving the SGP through a better accounting of public investment. Cambridge: Dept. of Economics.
Bokan, N., Hughes Hallett, A., & Jensen, S. E. H. (2016). Growth-Maximizing debt under changing demographics. Macroeconomic Dynamics, 20, 1640–1651.
de la Croix, D., & Michel, P. (2002). A Theory of Economic Growth. Cambridge Books.
Fatas, A., von Hagen, J., Hughes Hallett, A., Strauch, R. & Siebert, A. (2003). Stability and Growth in Europe: Towards a better pact. Monitoring European Integration 13, Centre for Economic Policy, London.
Hughes Hallett, A., Jensen, S. E. H., Sveinsson, T. S., & Vieira, F. (2019). Sustainable fiscal strategies under changing demographics. European Journal of Political Economy, 57, 34–52.
Kalaitzidakis, P., & Kalyvitis, S. (2004). On the macroeconomic implications of maintenance in public capital. Journal of Public Economics, 88, 695–712.
Kaldor, N. (1957). A Model of Economic Growth. The Economic Journal, 67(268), 591–624.
Yakita, A. (2008). Ageing and public capital accumulation. International Tax and Public Finance, 15, 582–598.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This article builds upon work originally started with Professor Andrew Hughes Hallett, who sadly passed away on December 31st, 2019, after a long fight with cancer. Completing this work is our modest attempt to pay tribute to a colleague, supervisor and friend. We gratefully acknowledge helpful comments provided by an anonymous referee. This research was supported by PeRCent, which receives base funding from the Danish pension funds and Copenhagen Business School.
Appendices
Appendix 1: Jacobian, Hessian, and Policy Function Partial Derivative
The Jacobian for the motion equation in (16) is:
The Hessian is:
The policy function partial derivative becomes:
Appendix 2: Evaluations of Jacobian, Hessian and Policy Function Partial at Maximum Growth Steady State and Under Steady State Condition
Here the evaluation of the stability implicit function criteria for the maximum growth steady state to be a tangent bifurcation is shown. As seen in de la Croix and Michel (2002), the conditions are:
where \( \varphi \left( {X_{t} ,\mathop {\dot{G}_{t} }\limits } \right) \equiv X_{t + 1} \left( {X_{t} ,\mathop {\dot{G}_{t} }\limits } \right) - X_{t}\).
Checking the conditions we see that they all hold:
\(\varphi_{X}^{^{\prime\prime}} \left( {X^{*} ,\gamma^{A} \left( {X^{*} } \right)} \right) = \frac{1}{2}\left\{ {\frac{{\alpha \omega^{2} }}{1 + C} - \frac{4\alpha }{{1 - \alpha + C}} - \omega^{2} + \frac{{\sqrt {4\alpha \left( {1 + C} \right) + \left( {1 - \alpha + C} \right)^{2} \omega^{2} } }}{{\left( {1 + C} \right)\left( {1 - \alpha + C} \right)}}\left[ {2 + \omega - \alpha \omega + C\left( {2 + \omega } \right)} \right]} \right\} > 0\) Overall, these characteristics prove that the maximum growth steady state is a tangent bifurcation.
Note that here it is also shown that \(\varphi_{{\dot{G}}}^{^{\prime}} \left( {X^{*} ,\gamma^{A} \left( {X^{*} } \right)} \right) > 0\) and \(\varphi_{X}^{{^{\prime\prime}}} \left( {X^{*} ,\gamma^{A} \left( {X^{*} } \right)} \right) > 0\). The sign of these two derivatives is important to assert the existence and stability of steady states in the vicinity of the maximum growth steady state, in that the motion equation is convex and next period’s capital ratio, \(X_{t + 1}\), decreases as the policy function \({\dot{G}}_{t}\) is reduced. Furthermore, since \(\varphi_{X}^{^{\prime}} \left( {X^{*} ,\gamma^{A} \left( {X^{*} } \right)} \right) = 0\) and \(\varphi_{X}^{{^{\prime\prime}}} \left( {X^{*} ,\gamma^{A} \left( {X^{*} } \right)} \right) > 0\), the Jacobian of the motion Eq. (16) near the point \({X}^{*}\) has a value lower than 1 for values below the maximum growth point \({X}^{*}\) and higher than 1 for \(X\) values bigger than \({X}^{*}\).
Appendix 3: Derivation of Demography-Related Partial Derivatives of \({{\varvec{X}}}^{\mathbf{*}}\)
The demography-related derivatives of \({X}^{*}\) are formally evaluated in Hughes Hallett et al. (2019). Summarizing their results:
Parameter | Derivative of \(X^{*}\) |
|---|---|
\(\rho\) | \(\frac{{\partial X^{*} }}{\partial \rho } = \underbrace {{X_{n}^{*} }}_{ > 0}\underbrace {{n_{\rho } }}_{ < 0} < 0\) |
\(\lambda\) | \(\frac{{\partial X^{*} }}{\partial \lambda } = \underbrace {{X_{n}^{*} }}_{ > 0}\underbrace {{n_{\lambda } }}_{ > 0} > 0\) |
\(\varepsilon\) | \(\frac{{\partial X^{*} }}{\partial \varepsilon } = \underbrace {{X_{n}^{*} }}_{ > 0}\underbrace {{n_{\varepsilon } }}_{ > 0} > 0\) |
\(\rho_{w}\) | \(\frac{{\partial X^{*} }}{{\partial \rho_{w} }} = \underbrace {{X_{{\rho_{w} }}^{*} }}_{ > 0} + \underbrace {{X_{n}^{*} n_{{\rho_{w} }} }}_{ > 0} > 0\) |
Using as short \({\Psi } = \frac{1}{2}\left( {\rho_{w} \frac{{\left( {1 - \alpha } \right)zn}}{{\alpha \left( {1 - zn} \right)}} + \frac{1 + \alpha }{\alpha }} \right) + \left( {\frac{1}{{\omega^{2} }} - 1} \right)\), the derivatives are:
Appendix 4: Calibration of Hughes Hallett et al. (2019)
Below are four tables from the calibration exercise in Hughes Hallett et al. (2019)
Parameter values of the baseline simulation | ||
|---|---|---|
\(\alpha\) | Private capital's share in national income | 0.37 |
\(\beta\) | Private capital’s importance in productivity factor | 0.55 |
\(\omega\) | Private capital elasticity in production | 0.716 |
\(A\) | TFP scale factor | 34 |
\(\rho\) | Subjective discount factor | 0.69 |
\(z\) | Rearing time per child | 0.281 |
\(\rho_{w}\) | Child-rearing subsidy rate | 0.193 |
\(\lambda\) | Death rate | 0.7 |
\(\varepsilon\) | Importance of children in utility | 0.539 |
Results of steady state baseline simulation | ||
|---|---|---|
\(d^{*}\) | Optimal debt to GDP ratio in steady state (no TFP) | 49.67% |
\(X\) | Public private capital ratio | 0.2546 |
\(\gamma^{A}\) | Annual economic growth rate | 1.44% |
\(\gamma\) | Annual economic growth rate per capita | 0.75% |
\(\theta\) | Tax rate | 14.5% |
\(\tilde{C}\) | Saving rate (out of disposable income) | 11.86% |
\(r\) | Annualized interest rate | 5.14% |
\(n\) | Number of children per person | 1.36 |
Old-age dependency ratio | 22% | |
Life expectancy at birth | 78.5 | |
Sensitivities to demographic parameters, OECD economies | ||
|---|---|---|
\(X_{n}^{*}\) | \(\partial {\text{X}}^{*} /\partial {\text{n}}\) | 0.0067 |
\({\text{n}}_{{\uplambda }}\) | \(\partial {\text{n}}/\partial {\uplambda }\) | 0.538 |
\({\text{n}}_{{\upvarepsilon }}\) | \(\partial {\text{n}}/\partial {\upvarepsilon }\) | 1.746 |
\({\text{n}}_{{\uprho }}\) | \(\partial {\text{n}}/\partial {\uprho }\) | −0.234 |
\({\text{d}}_{{\uplambda }}^{*}\) | \(\partial {\text{d}}^{*} /\partial {\uplambda }\) | 0.005 |
\({\text{d}}_{{\upvarepsilon }}^{*}\) | \(\partial {\text{d}}^{*} /\partial {\upvarepsilon }\) | 0.016 |
\({\text{d}}_{{\uprho }}^{*}\) | \(\partial {\text{d}}^{*} /\partial {\uprho }\) | −0.002 |
OECD population growth, old-age dependency ratios and life expectancy (45 year averages) | |||
|---|---|---|---|
1970–2015 | 2015–2060 | 2060–2100 | |
45-year population growth rate | 36.1% | 6.3% | −5.2% |
Old-age dependency ratio | 21.9% | 44.0% | 60.1% |
Life expectancy at birth | 75.2 | 83.9 | 89.2 |
Parameter \(\lambda \) | 0.7 | 0.532 | 0.43 |
Parameter \(\varepsilon \) | 0.539 | 0.42 | 0.382 |
\({X}^{*}\) | 25.5% | 25.3% | 25.2% |
\({d}^{*}\) | 49.7% | 49.4% | 49.3% |
Rights and permissions
About this article
Cite this article
Jensen, S.E.H., Sveinsson, T.S. & Vieira, F.B. From Here to There: Achieving Fiscal Sustainability Under Alternative Demographic Contingencies. De Economist 169, 427–444 (2021). https://doi.org/10.1007/s10645-021-09392-3
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10645-021-09392-3