Recurrent default or policy-optimal taxation

Abstract

This paper investigates the syndrome of “this time is different” with respect to Reinhart and Rogoff’s (This time is different: eight centuries of financial folly Princeton University Press, Princeton, 2011) interpretation of their extensive, historical data on financial default, and with particular regard to public debt in a closed-economy. Recurrent and over-generous promises to credulous investors of an ex ante, policy-optimal return amounts to an extra policy instrument in boosting the demand for public debt. In a numerical simulation of a version of the Diamond (Am Econ Rev 55:1126–1150, 1965) model, we find that the incentive for the policy-maker to pursue this strategy is trivial if taxes can be set at a policy-optimal level, but possibly over-riding if they cannot. Thus, the main result lines up with the empirical conclusion of Reinhart et al. (Debt intolerance. Debt intolerance, 2003) that “debt intolerant countries have weak fiscal structures”. The subsidiary result of the model is that defaulting countries will also have higher shares of public expenditure. Thus the model also predicts Wagner’s Law to the extent that fiscal structure is correlated with economic development.

Appendix: Solution

1.1 Factor prices, public expenditure and economic growth

For analytical convenience, we calculate the solutions sequentially, although this is not significant for the results. Returning to Eq. (9), $\begin{aligned} \ln Z_{t} = \ln \left( {(1 - \tau_{t} )w_{t} } \right) + \eta \ln \left( {\tau_{t} w_{t} + \beta_{t} \sigma (1 - \tau_{t} )w_{t} - g_{{_{t} }}^{P} - g_{t}^{N} } \right) \hfill \\ + \varpi \ln \left( {(1 - \beta_{t} )\sigma (1 - \tau_{t} )w_{t} } \right) + \gamma \ln g_{t}^{N} \hfill \\ \end{aligned}$, the policy-optimal level of non-productive public expenditure is

$$g_{{_{t} }}^{N} = \frac{\gamma }{\gamma + \eta }\left( {\tau_{t} w_{t} + \beta_{t} \sigma (1 - \tau_{t} )w_{t} - g_{t}^{P} } \right) .$$

(12)

Substituting this back into (9) gives

$$\begin{aligned} \ln Z^{\prime}_{t} = \ln \left( {(1 - \tau_{t} )w_{t} } \right) + (\eta + \gamma )\ln \left( {\tau_{t} w_{t} + \beta_{t} \sigma (1 - \tau_{t} )w_{t} - g_{{_{t} }}^{P} } \right),\;{\text{or}} \hfill \\ \quad+ \varpi \ln \left( {(1 - \beta_{t} )\sigma (1 - \tau_{t} )w_{t} } \right) + \cdots \hfill \\ \quad\ln Z^{\prime}_{t} = \ln (1 - \tau_{t} ) + (\eta + \gamma )\ln \left( {\tau_{t} + \beta_{t} \sigma (1 - \tau_{t} ) - {{g_{{_{t} }}^{P} } \mathord{\left/ {\vphantom {{g_{{_{t} }}^{P} } {w_{t} }}} \right. \kern-0pt} {w_{t} }}} \right) \hfill \\ \quad+ \varpi \ln \left( {(1 - \beta_{t} )\sigma (1 - \tau_{t} )} \right) + (1 + \eta + \gamma + \varpi )\ln w_{t} \hfill \\ \end{aligned}$$

(13)

Substituting (5) for the wage into (13) gives

$$\begin{aligned} \ln Z^{\prime\prime}_{t} = \ln (1 - \tau_{t} ) + (\eta + \gamma )\ln \left( {\tau_{t} + \beta_{t} \sigma (1 - \tau_{t} ) - \frac{{g_{t}^{P\mu } }}{{(1 - \mu )Ak_{t}^{\mu } }}} \right) \hfill \\ + \varpi \ln \left( {(1 - \beta_{t} )\sigma (1 - \tau_{t} )} \right) + (1 + \eta + \gamma + \varpi )(1 - \mu )\ln g_{t}^{P} + \cdots \hfill \\ \end{aligned}$$

(14)

The policy-optimal level of productive public expenditure is

$$g_{t}^{P} = \left( {\frac{{(1 - \mu )^{2} (1 + \eta + \gamma + \varpi )\left( {\tau_{t} + \beta_{t} \sigma (1 - \tau_{t} )} \right)A}}{\mu (\eta + \gamma ) + (1 - \mu )(1 + \eta + \gamma + \varpi )}} \right)^{{\frac{1}{\mu }}} k_{t} ,$$

(15)

which, according to (5) implies a wage and an expected value return on capital of

$$w_{t} = (1 - \mu )A\left( {\frac{{(1 - \mu )^{2} (1 + \eta + \gamma + \varpi )\left( {\tau_{t} + \beta_{t} \sigma (1 - \tau_{t} )} \right)A}}{\eta + \gamma + (1 - \mu )(1 + \varpi )}} \right)^{{\frac{1}{\mu } - 1}} k_{t} ,$$

(16)

$$E_{t - 1} \left(R_{{_{t} }}^{K} \right) = \mu \left( {\frac{{(1 - \mu )^{2} (1 + \eta + \gamma + \varpi )\left( {\tau_{t} + \beta_{t} \sigma (1 - \tau_{t} )} \right)}}{\eta + \gamma + (1 - \mu )(1 + \varpi )}} \right)^{{\frac{1}{\mu } - 1}} A^{{{1 \mathord{\left/ {\vphantom {1 \mu }} \right. \kern-0pt} \mu }}}$$

(17)

The ratio of the productive public expenditure to the wage is

$$\frac{{g_{t}^{P} }}{{w_{t} }} = \left( {\frac{(1 - \mu )(1 + \eta + \gamma + \varpi )}{\eta + \gamma + (1 - \mu )(1 + \varpi )}} \right)\left( {\tau_{t} + \beta_{t} \sigma (1 - \tau_{t} )} \right)$$

(18)

Equations (12) and (18) imply the equivalent ratio for total public expenditure,

$$\frac{{g_{t} }}{{w_{t} }} = \frac{{g_{t}^{P} + g_{t}^{N} }}{{w_{t} }} = \left( {\frac{\eta (1 - \mu ) + \gamma + (1 - \mu )(1 + \varpi )}{\eta + \gamma + (1 - \mu )(1 + \omega )}} \right)\left( {\tau_{t} + \beta_{t} \sigma (1 - \tau_{t} )} \right)$$

(19)

Equations (14) and (15) give

$$\ln Z^{\prime\prime\prime}_{t} = \ln (1 - \tau_{t} ) + \varPsi \ln \left( {\tau_{t} + \beta_{t} \sigma (1 - \tau_{t} )} \right) + \varpi \ln \left( {(1 - \beta_{t} )\sigma (1 - \tau_{t} )} \right) + ..$$

$$\varPsi \equiv \left( {(\eta + \gamma ) + \frac{1 - \mu }{\mu }\left( {1 + \eta + \gamma + \varpi } \right)} \right)$$

(20)

Equations (2) and(16) give the growth factor for the capital stock as

$$\frac{{k_{t} }}{{k_{t - 1} }} = (1 - \mu )(1 - \beta_{t - 1} )\sigma (1 - \tau_{t - 1} )A^{{^{{{1 \mathord{\left/ {\vphantom {1 \mu }} \right. \kern-0pt} \mu }}} }} \left( {\frac{{(1 - \mu )^{2} \left( {\tau_{t - 1} + \beta_{t - 1} \sigma (1 - \tau_{t - 1} )} \right)}}{{\frac{\mu (\eta + \gamma )}{1 + \eta + \gamma + \varpi } + 1 - \mu }}} \right)^{{{1 \mathord{\left/ {\vphantom {1 \mu }} \right. \kern-0pt} \mu } - 1}}$$

(21)

1.2 Actual ex post returns on public debt

Equations (8) and (19) give

$$R_{t}^{B} = \left( {\frac{\eta \mu }{\eta + \gamma + (1 - \mu )(1 + \omega )}} \right)\left( {\frac{{\tau_{t} + \beta_{t} \sigma (1 - \tau_{t} )}}{{\beta_{t - 1} \sigma (1 - \tau_{t - 1} )}}} \right)\frac{{w_{t} }}{{w_{t - 1} }}$$

(22)

Equation (16) implies a factor of wage growth of

$$\frac{{w_{t} }}{{w_{t - 1} }} = \left( {\frac{{\tau_{t} + \beta_{t} \sigma (1 - \tau_{t} )}}{{\tau_{t - 1} + \beta_{t - 1} \sigma (1 - \tau_{t - 1} )}}} \right)^{{{1 \mathord{\left/ {\vphantom {1 \mu }} \right. \kern-0pt} \mu } - 1}} \frac{{k_{t} }}{{k_{t - 1} }}$$

(23)

The last three equations imply

$$R_{t}^{B} = \frac{{\eta \mu (1 - \mu )\left( {(1 + \eta + \gamma + \varpi )(1 - \mu )^{2} } \right)^{{{1 \mathord{\left/ {\vphantom {1 {\mu - 1}}} \right. \kern-0pt} {\mu - 1}}}} }}{{\left( {\eta + \gamma + (1 - \mu )(1 + \varpi )} \right)^{{{1 \mathord{\left/ {\vphantom {1 \mu }} \right. \kern-0pt} \mu }}} }}\left( {\frac{{1 - \beta_{t - 1} }}{{\beta_{t - 1} }}} \right)\left( {\tau_{t} + \beta_{t} \sigma (1 - \tau_{t} )} \right)^{{{1 \mathord{\left/ {\vphantom {1 \mu }} \right. \kern-0pt} \mu }}} A^{{{1 \mathord{\left/ {\vphantom {1 \mu }} \right. \kern-0pt} \mu }}}$$

(24)

This can be expressed in relation to $E_{t - 1} (R_{{_{t} }}^{K} )$ in Eq. (17) as

$$R_{t}^{B} = \frac{{\eta \mu (1 - \mu )\left( {(1 + \eta + \gamma + \varpi )(1 - \mu )^{2} } \right)^{{{1 \mathord{\left/ {\vphantom {1 {\mu - 1}}} \right. \kern-0pt} {\mu - 1}}}} }}{{\left( {\eta + \gamma + (1 - \mu )(1 + \varpi )} \right)^{{{1 \mathord{\left/ {\vphantom {1 \mu }} \right. \kern-0pt} \mu }}} }}\left( {\frac{{1 - \beta_{t - 1} }}{{\beta_{t - 1} }}} \right)\left( {\tau_{t} + \beta_{t} \sigma (1 - \tau_{t} )} \right)^{{{1 \mathord{\left/ {\vphantom {1 \mu }} \right. \kern-0pt} \mu }}} A^{{{1 \mathord{\left/ {\vphantom {1 \mu }} \right. \kern-0pt} \mu }}}$$

$$E_{t - 1} (R_{{_{t} }}^{K} ) = \mu \left( {\frac{{(1 - \mu )^{2} (1 + \eta + \gamma + \varpi )\left( {\tau_{t} + \beta_{t} \sigma (1 - \tau_{t} )} \right)}}{\eta + \gamma + (1 - \mu )(1 + \varpi )}} \right)^{{\frac{1}{\mu } - 1}} A^{{{1 \mathord{\left/ {\vphantom {1 \mu }} \right. \kern-0pt} \mu }}}$$

$$\frac{{R_{t}^{B} }}{{E_{t - 1} (R_{t}^{K} )}} = \varGamma \left( {\frac{{1 - \beta_{t - 1} }}{{\beta_{t - 1} }}} \right)\left( {\tau_{t} + \beta_{t} \sigma (1 - \tau_{t} )} \right),\;\varGamma \equiv \frac{\eta (1 - \mu )}{\eta + \gamma + (1 - \mu )(1 + \varpi )} ,$$

(25)

1.3 Public debt under rational expectations

King expectations of the future value of the ration (25), while assuming E _t (τ _t+1) = τ _t and E _t (β _t+1) = β _t gives

$$\frac{{E_{t} (R_{t + 1}^{B} )}}{{E_{t} (R_{t + 1}^{K} )}} = \varGamma \left( {\frac{{1 - \beta_{t} }}{{\beta_{t} }}} \right)\left( {\tau_{t} + \beta_{t} \sigma (1 - \tau_{t} )} \right),\;\quad\varGamma \equiv \frac{\eta (1 - \mu )}{\eta + \gamma + (1 - \mu )(1 + \varpi )}$$

This is solved simultaneously with (3) gives a quadratic equation for the portfolio share of public debt, β _t ,

$$\varGamma \sigma (1 - \tau_{t} )\beta_{t}^{2} + \left( {1 + \varGamma \left( {\tau_{t} - \sigma (1 - \tau_{t} )} \right)} \right)\beta_{t} - \frac{\alpha }{1 + \alpha } - \varGamma \tau_{t} = 0$$

(26)

1.4 Public debt under manipulation of beliefs

As $\tilde{\beta }_{t}$ is a positive monotonic function of $_{t} \tilde{R}_{t + 1}^{B}$, we consider its value that maximizes (20),

$$\tilde{\beta }_{t} = \frac{{\varPsi + {{(\varpi } \mathord{\left/ {\vphantom {{(\varpi } \sigma }} \right. \kern-0pt} \sigma })\left( {1 - (1 - \tau_{t} )^{ - 1} } \right)}}{\varPsi + \varpi },\quad\varPsi \equiv \left( {(\eta + \gamma ) + \frac{1 - \mu }{\mu }\left( {1 + \eta + \gamma + \varpi } \right)} \right),$$

(27)

which according to (3) requires a promised return factor of

$$_{t} \tilde{R}_{{_{t + 1} }}^{B} = \left( {1 - \left( {\frac{\alpha }{1 + \alpha }} \right)\left( {\frac{\varPsi + \omega }{{\varPsi - ({\varpi \mathord{\left/ {\vphantom {\varpi \sigma }} \right. \kern-0pt} \sigma }){{\tau_{t} } \mathord{\left/ {\vphantom {{\tau_{t} } {(1 - \tau_{t} )}}} \right. \kern-0pt} {(1 - \tau_{t} )}}}}} \right)} \right)E_{t} (R_{t + 1}^{K} )$$

(28)

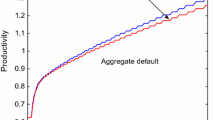
This is lagged one period then divided by the actual return in (25) to give the default ratio

$$\frac{{_{t - 1} \tilde{R}_{{_{t} }}^{B} }}{{R_{t}^{B} }} = \frac{{\varPsi - \alpha \omega - \left( {\varPsi + \varpi \left( {(1 + \alpha )\sigma^{ - 1} - \alpha } \right)} \right)\tau_{t - 1} }}{{\varpi \varGamma (1 + \alpha )\left( {1 + (\sigma^{ - 1} - 1)\tau_{t - 1} } \right)\left( {\tau_{t} + \beta_{t} \sigma (1 - \tau_{t} )} \right)}}$$

(29)

1.5 Policy-optimal taxes

Returning to Eq. (20), the policy-maker’s preference for taxation is the rate

$$1 - \tau_{t} = \frac{\varPi }{{1 - \sigma \beta_{t} }},{\text{ where}}\;\;\varPi \equiv \frac{\mu (1 + \varpi )}{1 + \eta + \gamma + \varpi } .$$

(30)

Under policy-optimal taxes, Eq. (27) for rational beliefs becomes,

$$\beta = \frac{{{\alpha \mathord{\left/ {\vphantom {\alpha {(1 + \alpha )}}} \right. \kern-0pt} {(1 + \alpha )}} + (1 - \varPi )\varGamma }}{1 + (1 - \varPi )\varGamma },\;\varGamma \equiv \frac{\eta (1 - \mu )}{\eta + \gamma + (1 - \mu )(1 + \varpi )}$$

(31)

implying optimal taxes in this case of

$$\tilde{\tau }_{t} = 1 - \frac{\mu }{(1 + \varpi + \eta + \gamma )(1 - \sigma )} .$$

(32)

1.6 Public welfare with the optimal levels of the expenditures

Returning to Eqs. (18) and (19), where $g_{t}^{P} = \kappa^{P} \left( {\tau_{t} + \beta_{t} \sigma \left( {1 - \tau_{t} } \right)} \right)\,w_{t}$, where $\kappa^{P} \equiv \frac{(1 - \mu )(1 + \eta + \gamma + \varpi )}{\eta + \gamma + (1 - \mu )(1 + \varpi )}$, and $g_{t}^{N} = \kappa^{N} \left( {\tau_{t} + \beta_{t} \sigma \left( {1 - \tau_{t} } \right)} \right)w_{t}$, where $\kappa^{N} \equiv \frac{\mu \gamma }{\eta + \gamma + (1 - \mu )(1 + \varpi )}$,means Eq. (7) becomes

$$\begin{aligned} \ln Z_{t} = \ln (1 - \tau_{t} ) + \eta \ln (1 - \kappa^{P} - \kappa^{N} )\left( {\tau_{t} + \beta_{t} \sigma (1 - \tau_{t} )} \right) \hfill \\ + \omega \ln \left( {(1 - \beta_{t} )\sigma (1 - \tau_{t} )} \right) + \gamma \ln \left( {\kappa^{N} \left( {\tau_{t} + \beta_{t} \sigma (1 - \tau_{t} )} \right)} \right) + (1 + \eta + \varpi + \gamma )\ln w_{t} \hfill \\ \end{aligned}$$

(33)

Since Eq. (5) and $g_{t}^{P} = \kappa^{P} \left( {\tau_{t} + \beta_{t} \sigma \left( {1 - \tau_{t} } \right)} \right)w_{t}$ imply

$$w_{t} = \frac{1}{\mu }\ln \left( {(1 - \mu )A} \right) + \left( {\frac{1 - \mu }{\mu }} \right)\ln \left( {\kappa^{P} \left( {\tau_{t} + \beta_{t} \sigma (1 - \tau_{t} )} \right)} \right) + \ln k_{t} ,$$

(34)

Eq. (33) is finally presented as

$$\begin{aligned} \ln Z_{t} = (1 + \varpi )\ln (1 - \tau_{t} ) + \varpi \ln (1 - \beta_{t} ) \hfill \\ + \left( {\eta + \gamma + \left( {\frac{1 - \mu }{\mu }} \right)(1 + \eta + \varpi + \gamma )} \right)\ln \left( {\tau_{t} + \beta_{t} \sigma (1 - \tau_{t} )} \right) + .. \hfill \\ \end{aligned} ,$$

(35)

which is the basis for calculating the gains.