Harvesting the Commons

Abstract

We study a socio-ecological model in which a continuum of consumers harvest a common property renewable natural resource. Markov perfect Nash equilibria of the corresponding non-cooperative game are derived and are compared with collectively optimal harvesting policies. The underlying mechanisms that drive open-access commons in our model are shaped by population size, harvesting costs, and the ecosystem’s productivity. If other things equal population is small relative to harvesting costs, unmanaged commons do not face destruction. More strikingly, they are harvested at the collectively optimal rate. Property rights do not matter in that parametric regime because the resource has no social scarcity value. However, if other things equal population is large relative to harvesting costs, open-access renewable natural resources suffer from the tragedy of the commons. Property rights matter there because the resource has a social scarcity price. The population size relative to harvesting costs at which the socio-ecological system bifurcates is an increasing function of the ecosystem’s productivity. A sudden crash in productivity, population overshoot, or decline in harvesting costs can tip an unmanaged common into ruin. The model provides a way to interpret historical and archaeological findings on the collapse of those societies that have been studied by scholars.

1 The Problem

The economic theory of common-property resources, or “commons” for short, has for the most part remained confined to a timeless setting. Dasgupta and Heal (1979: Ch. 3) formulated the situation to be studied as a one-stage symmetric game involving herdsmen grazing their cattle on a piece of communal land. It was shown that if, as is typically the case in village grazing fields in South Asia and sub-Saharan Africa, access to the common is restricted to a well-defined group of herdsmen, the implicit rent each herdsman earns in a non-cooperative equilibrium is less than what each would have enjoyed had they cooperated. The authors also showed that if the size of the group was to increase indefinitely, each herdsman would introduce a vanishingly small herd, but the total number of cattle in the field would expand to the point where aggregate rent is zero. The distortion created by each herdsman is no doubt small if the group size is large, but the sum of those small distortions is not small.

The situation where access to a common is unrestricted was first studied by Gordon (1954). Although he did not offer a formal analysis, the methods deployed by Dasgupta and Heal (1979) can be extended to complete his account. Suppose the number of potential herdsmen is unlimited but entry into the common involves a small fixed cost. The situation can be modelled as a two-stage non-cooperative game: Herdsmen decide whether to enter, following which those who have entered choose the size of their herds. It can be shown that in symmetric sub-game perfect Nash equilibria the number of herdsmen who enter tends to infinity and the aggregate rent from grazing the common tends to zero as the cost of entry becomes vanishingly small.

Rent dissipation is a reflection of overgrazing. But there is a further concern, that in time overgrazing could lead to the common’s destruction even if it was in the herdsmen’s collective interest to preserve it over an indefinite future. The situation would be as though each herdsman discounts the output from the commons at a higher rate than he would have, had the group acted collectively. In his famous paper on open-access resources, Hardin (1968) implicitly considered a dynamic setting. The grazing field can then be thought of as a renewable natural resource. If the rate at which cattle consume fodder exceeds the field’s regenerative capacity by a finite margin, it is doomed. Although Hardin (1968) did not offer a formal analysis, he insisted that unrestricted freedom in the commons leads in time to their ruin. And he dubbed the processes unleashed by that freedom, the “tragedy of the commons”.¹

Identifying Hardin’s processes in situations where agents choose the size of their herds strategically over time has not been found to be easy; which is why the theoretical literature on the fate of commons in dynamic settings remains sparse.² It has been customary to study strategic behaviour among a group of identical agents consuming a common-property renewable natural resource. The payoff to an agent is the discounted sum of net utilities (utility minus harvesting costs) over time. Utility is assumed to be a monotonically increasing, concave function of personal consumption, and harvesting costs are linear and independent of the resource stock.³ The optimal rate of resource exploitation when the agents fully cooperate has been characterized by Clark (2010). The idea here, on the other hand, is to determine (symmetric) Markov perfect Nash equilibria of the corresponding non-cooperative game. Computation of equilibria has proved to be hard. Particular forms of the utility function have been assumed so as to obtain clear results concerning the circumstances in which the resource would be exhausted in finite time even when preservation is in the collective interest. Those results identify, conversely, the circumstances in which a common would be preserved indefinitely even if consumers were not to cooperate.

To see how far informed intuition can help us to probe the fate of common-property resources, notice that it would be collectively optimal to deplete a renewable natural resource if its growth rate at the point where the stock is vanishingly small (call it r) were less than the rate at which agents discount the future (call it $\delta$).⁴ But if it is in the collective interest to deplete a resource, then other things equal non-cooperation among the agents should be expected all the more to lead to its depletion. The theoretically interesting case for study is thus $r>\delta ;$ which is what we assume throughout this paper. Our aim is to uncover the circumstances in which non-cooperation leads to resource depletion even though it is in the collective interest to preserve it. We also want to identify those circumstances where a resource would be preserved indefinitely even if users were not to cooperate.

The economics of common-property resources in a timeless setting tells us that the group’s size (call it N) is a critical factor. Because N is finite, each agent’s consumption has a discernible, negative impact on others’ welfare. The larger is N, however, the smaller is an individual’s impact on others even while aggregate consumption is larger. That suggests the larger is N, the greater is the wedge between the fate of a common under cooperation and non-cooperation, respectively. Assuming that $r>\delta$, the question arises whether there is a threshold value of r (call it h(N)), such that under non-cooperation a common would be preserved if $r>h(N)$ but would be ruined if $r<h(N)$. In their analysis of a complete capital model, Mitra and Sorger (2014) obtained the precise form of h(N) and showed that it is an increasing function of N.

The informal picture of an open-access resource that Hardin (1968) drew is however of a common that is teeming with people because of unrestricted entry. It is then tempting to uncover the fate of open-access resources by letting N go to infinity. That is the route Dasgupta and Heal (1979: Ch. 3) took in their timeless model.

If N is large, each person’s equilibrium consumption is no doubt small, but the resource to population ratio is also small. In the limit the resource to population ratio is zero, which is an awkward feature of the model.

2 Open-Access Renewable Natural Resources: A Formulation

In order to avoid the awkwardness mentioned at the end of the previous section, we move in an altogether different direction here. Instead of working with a finite number of agents, we study the behaviour of a continuum of agents. The continuum is the cleanest demographic assumption to make for testing our intuitions on the fate of unmanaged common-property resources, because each agent in the continuum is entirely negligible. Consequently, there is no scope for strategic behavior between the harvesters, which seems to be a more realistic setting than the game-theoretic models dominating the literature. Moreover, we can study the effect of the size of the human population on common-property resources by varying the population’s measure, which we denote by N.

For vividness we will read renewable natural resources as ecosystems, measured in units of biomass. Fisheries are a familiar example, forests are another. The resource is harvested for consumption, but harvesting involves costs, the unit harvesting cost being $\alpha >0$. It is assumed that $\alpha$ is independent of the stock of the resource and that storage ex situ is prohibitively costly.

Although the model we construct is stark, we want it to make connection with the historical experience of a broad range of open-access resources. In centuries past human numbers were small and harvesting technologies were primitive. Over time numbers grew (N increased) and harvesting technologies improved ($\alpha$ declined). Both parameters are assumed here to change slowly. The assumption enables us to treat N and $\alpha$ as constants within the time frame of socio-ecological dynamics. We are then able to study the fate of unmanaged commons, derive collectively optimum harvesting policies, and trace both to N and $\alpha$, and in turn identify the role played by the ecosystem’s productivity and the rate at which consumers discount the future ($\delta$). Productivity is measured in terms of the ecosystem’s “primary production”. In a famous two-parameter formulation of productivity, known as the r–K model (which we study presently), primary production at any value of biomass is determined by r (defined above) and its capacity to supply the consumption good (we denote that by K).⁵

Our central findings are as follows:

• (1) Other things equal if N is small relative to $\alpha$, unmanaged renewable natural resources do not suffer from the tragedy of the commons. The commons are not only conserved, they are harvested at the collectively optimal rate (Propositions 1 and 3). Property rights do not matter because when N is small relative to $\alpha$ ecosystems have no social scarcity value. However, if other things equal N is large relative to $\alpha$, unmanaged renewable natural resources suffer from the tragedy of the commons. Freedom in the commons leads to their depletion in finite time even though it is in the collective interest to enforce a sustainable consumption policy (Propositions 2 and 4). Property rights matter when N is large relative to $\alpha$ because ecosystems have a positive social scarcity price. Population overshoot that can follow a rise in food production has been found to be a trigger for the subsequent collapse of a number of past civilisations (see Sect. 5).

• (2) The value of N at which the socio-ecological system bifurcates into the two regimes is not only an increasing function of the harvesting cost $\alpha$ but also of the ecosystem’s productivity. For reasons we have given, it is assumed throughout that the resource’s intrinsic growth rate, r, exceeds the rate at which consumers discount the future, $\delta$. It follows that a sudden crash in the ecosystem’s productivity (drought, pestilence) can tip an unmanaged common to a ruinous path. Soil erosion and climate change have been identified as causes of the collapse of a number of early civilisations (see Sect. 5). Habitat destruction owing to its conversion into other forms of capital (conversion of wetlands into urban habitation) is another cause of a decline in ecosystem productivity. In contrast, contemporary advances in bio-technology increase an ecosystem’s productivity.⁶

• (3) Harvesters’ time preference $\delta$ affects the collectively optimal consumption programme if N is large relative to $\alpha$; otherwise $\delta$ has no influence on the consumption trajectories (but see Remark 1 below). So long as $r>\delta$, myopia should not be used to explain unsustainable resource consumption (Propositions 1–4).

2.1 Ecosystem Dynamics

Time is continuous and denoted by $t\in \mathbb {R}_{+}$. We denote the stock of the renewable natural resource available at time t by $X(t)\in \mathbb {R}_{+}$. Because ecosystems are the objects of interest here, X(t) is expressed in units of biomass.

In the absence of human predation, the ecosystem’s dynamics are governed by the equation

$$\begin{aligned} \mathrm{d}X(t)/\mathrm{d}t=G(X(t)). \end{aligned}$$

(1)

In Eq. (1),

$$\begin{aligned} \begin{array}{l} (i)\;G:\mathbb {R}_{+}\mapsto \mathbb {R}\text { is a twice continuously differentiable}\\ \qquad \text {and strictly concave function}, \\ (ii)\;\text {there exists }K>0\text {, such that }G(0)=G(K)=0,\ \\ \qquad \text {with }G(X)>0\text { for }X\in (0,K)\text { and }G(X)<0\text { for } X>K. \end{array} \end{aligned}$$

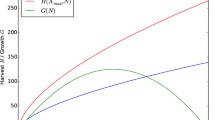
Expanding G(X) around $X=0$ in Eq. (1) tells us that $G^{\prime }(0)$ is the percentage rate of growth of the resource stock when X is small. $G^{\prime }(0)$ equals what we have been calling r. A graphical representation of primary production is given in Fig. 1.⁷

Example 2.1

An often used functional form of G is the quadratic polynomial

$$\begin{aligned} G(X)=rX[1-(X/K)], \end{aligned}$$

(2)

where $r=G'(0)$ and K are positive parameters referred to as the intrinsic growth rate of the resource and the carrying capacity of the ecosystem (i.e., the ecosystem’s capacity for providing the consumption good), respectively. Equation (2) is commonly known as the r–K model. $\square$

Fig. 1

Primary production as a function of X

Equation (1) has a unique stable fixed point, $X=K$. The initial stock of the resource, X(0), will be considered to lie in the interval [0, K].

2.2 Consumption and Welfare

There exists a continuum of identical harvesters. Each harvester is of measure 0, while the total population is of measure N. Without loss of generality we may describe the set of harvesters by the compact interval [0, N] and associate a unique harvester to each $i\in [0,N]$.

If $c\in \mathbb {R}_{+}$ is the rate at which a representative agent consumes the resource, her utility flow net of harvesting costs is

$$\begin{aligned} v(c)=u(c)-\alpha c. \end{aligned}$$

We assume:

$$\begin{aligned} \left. \begin{array}{l} (i)\;u:\mathbb {R}_{+}\mapsto \mathbb {R}\text { is twice-continuously differentiable and bounded below} \\ \qquad \text {with }u(0)=0,\;u^{\prime }(c)>0,\text { and }u^{\prime \prime }(c)<0\;\text {on } \mathbb {R}_{++}, \\ (ii)\;\lim _{c\rightarrow 0}u^{\prime }(c)=+\infty \text { and }\lim _{c\rightarrow +\infty }u^{\prime }(c)=0. \end{array} \right\} \end{aligned}$$

(3)

Figure 2 depicts the utility and the cost, respectively, of harvesting.

Example 2.2

A typical example of a function u satisfying the assumptions in (3) is given by the normalised iso-elastic function

$$\begin{aligned} u(c)=c^{1-\beta }/(1-\beta ) \end{aligned}$$

(4)

with the taste parameter $\beta$ satisfying $0<\beta <1$.$\square$

If c(t) is the representative agent’s consumption rate at t, her dynastic welfare is

$$\begin{aligned} \int _{0}^{\infty }v(c(t))e^{-\delta t}\,\mathrm{d}t \end{aligned}$$

with the time-preference rate $\delta$ satisfying $0<\delta <G^{\prime }(0)$.

Fig. 2

Utility and cost of harvesting

2.3 Ecosystem Dynamics and Human Activity

Aggregate consumption at time t is

$$\begin{aligned} C(t)=\int _0^Nc_i(t)\,\mathrm{d}i, \end{aligned}$$

where $c_i(t)$ denotes the consumption rate of harvester i at time t. The dynamics of the ecosystem under human predation is therefore

$$\begin{aligned} \mathrm{d}X(t)/\mathrm{d}t=G(X(t))-C(t)\,,\;X(0)\in [0,K]. \end{aligned}$$

(5)

In Eq. (5), $\mathrm{d}X(t)/\mathrm{d}t$ is the ecosystem’s net primary production at t.

Steady states of Eq. (5) are of particular interest, because they describe sustainable aggregate consumption rates. Denote the maximum of those sustainable consumption rates, which is also known as the maximum sustainable yield (MSY), by $C^{*}$. Defining $X^*$ as the unique (positive) number satisfying $G^{\prime }(X^*)=0$, it holds that $C^{*}=G(X^*)$. Both $X^*$ and $C^*$ are illustrated in Fig. 1.

Illustration 1

In the r–K model, i.e., if G(X) is given by Eq. (2), then it holds that $X^*=K/2$ and $C^{*}=rK/4$. One can see that in the context of this model, the MSY $C^*$ is linearly increasing in both the intrinsic growth rate of the resource, r, and in the ecosystem’s carrying capacity, K. $\square$

2.4 Threshold Values

The conditions in (3) imply that there exists a unique value of c at which the net utility $v(c)=u(c)-\alpha c$ is maximised. That value, which will be denoted by $c_\alpha$, is determined as the unique (positive) solution of the equation $u^{\prime }(c)=\alpha$ (see Fig. 2 for an illustration). It follows from the conditions in (3) that

$$\begin{aligned} \left. \begin{array}{l} (i)\;c_{\alpha }\;\text {is continuous and strictly decreasing with respect to }\alpha , \\ (ii)\;\lim _{\alpha \rightarrow 0}c_{\alpha }=+\infty \text { and }\lim _{\alpha \rightarrow +\infty }c_{\alpha }=0. \end{array} \right\} \end{aligned}$$

(6)

The properties of the function $c_{\alpha }$ stated in (6) imply that there is a unique value of $\alpha$, call it $\alpha ^{*}$, such that $c_{\alpha }=C^{*}/N$ holds at $\alpha =\alpha ^{*}$. Combining the defining equations of $c_\alpha$ and $\alpha ^*$, one obtains $\alpha ^*=u'(c_{\alpha ^*})=u'(C^*/N)$, which shows that $\alpha ^*$ is the marginal utility at the per-capita MSY. Note that this value depends on the utility function u, on the primary production G (via the MSY $C^*$), and on the population size N, but that it is independent of the time-preference rate $\delta$.

The threshold value $\alpha ^*=u'(C^*/N)$ will play an important role in our analysis. In Sects. 3 and 4 below, where non-cooperative and cooperative harvesting policies, respectively, are analysed, we demonstrate that $\alpha ^*$ forms a bifurcation point for the socio-ecological system. If $\alpha \ge \alpha ^{*}$, the rates at which the resource is consumed in the two institutional settings are the same: property rights do not matter. If on the other hand $\alpha <\alpha ^{*}$, non-cooperation ruins the common in finite time, whereas cooperation preserves it: property rights do matter.

For the interpretation of some of our results it will be more convenient to treat the population size N as the bifurcation parameter and to keep the extraction cost $\alpha$ fixed. To this end consider the following equivalence relations:

$$\begin{aligned}(\alpha <\alpha ^*)\Leftrightarrow (c_\alpha>C^*/N)\Leftrightarrow \left( N>\frac{C^*}{(u')^{-1}(\alpha )}\right) .\end{aligned}$$

The harvesting cost $\alpha$ is smaller than the threshold value $\alpha ^*$ if and only if the population size is larger than the corresponding threshold value $N^*=C^*/[(u')^{-1}(\alpha )]$. Note that $N^*$ is an increasing function of both the productivity of the ecosystem (as measured by $C^*$) and the extraction cost $\alpha$. The threshold values $\alpha ^*$ and $N^*$, respectively, form an increasing function in the $(\alpha ,N)$-parameter space as shown in Fig. 3.

Fig. 3

The threshold curve in the $(\alpha ,N)$-parameter space

Illustration 2

Suppose that the utility function u is of the iso-elastic form specified in Eq. (4). Then $c_{\alpha }=\alpha ^{-1/\beta }$ and, consequently, it follows that $\alpha ^{*}=(C^{*}/N)^{-\beta }$. If we assume in addition that the resource dynamics are given by the r–K model, then we can express $\alpha ^*$ as a function of the fundamentals N, r, K, and $\beta$ as follows:

$$\begin{aligned}\alpha ^*=\left( \frac{4N}{rK}\right) ^{\beta }.\end{aligned}$$

Analogously, we can express $N^*$ as a function of $\alpha$, r, K, and $\beta$ in the form

$$\begin{aligned}N^*=\frac{rK\alpha ^{1/\beta }}{4}.\end{aligned}$$

$\square$

2.5 Critical Resource Stocks

The properties of the function G together with the definitions of $C^*$, $c_\alpha$, and $\alpha ^*$ imply that for $\alpha <\alpha ^*$ there does not exist any resource stock X such that $G(X)=Nc_\alpha$. For $\alpha =\alpha ^*$, there is exactly one such resource stock, namely $X=X^*$. Finally, for $\alpha >\alpha ^*$, there exist two solutions of the equation $G(X)=Nc_\alpha$. We denote the smaller one by $\underline{X}_\alpha$ and the larger one by $\bar{X}_\alpha$ (see Fig. 1 for a graphical illustration in the case where $\alpha >\alpha ^*$). It is easy to see that $\underline{X}_\alpha$ is strictly decreasing with respect to $\alpha \in (\alpha ^*,+\infty )$, whereas $\bar{X}_\alpha$ is strictly increasing. Moreover, it holds that $\lim _{\alpha \rightarrow \alpha ^*}\underline{X}_{\alpha ^*}=\lim _{\alpha \rightarrow \alpha ^*}\bar{X}_{\alpha ^*}=X^*$, $\lim _{\alpha \rightarrow +\infty }\underline{X}_\alpha =0$, and $\lim _{\alpha \rightarrow +\infty }\bar{X}_\alpha =K$.

Illustration 3

Consider the r–K model. The critical resource stocks introduced above are given by

$$\begin{aligned} \underline{X}_\alpha =\frac{K\left[ r-\sqrt{r^2-(4Nrc_\alpha /K)}\,\right] }{2r}\in (0,K/2) \end{aligned}$$

and

$$\begin{aligned} \bar{X}_\alpha =\frac{K\left[ r+\sqrt{r^2-(4Nrc_\alpha /K)}\,\right] }{2r}\in (K/2,K). \end{aligned}$$

$\square$

3 Harvesting the Unmanaged Common

In what follows we assume that at any date $t\in \mathbb {R}_+$, for anyone to verify what others have harvested involves a small individual cost, say $\varepsilon >0$. The figure for the aggregate stock, X, is however assumed to be published regularly by the government. So X(t) is common knowledge at each time t. These two assumptions together with the stationarity of the problem provide a justification for assuming that the harvesters use stationary Markovian strategies, i.e., that they condition their consumption rates at any time t on the current stock of the resource X(t) only. The most popular equilibrium concept in such a setting is that of a Markov perfect Nash equilibrium, which requires that every player’s strategy is a best response to all her opponents’ strategies for any possible value of the state variable X.⁸ We have the following result:

Lemma 1

There exists a unique Markov perfect Nash equilibrium. This equilibrium is symmetric, i.e., all the players use the same strategy. The equilibrium strategy requires every player to consume at the constant rate $c_\alpha$ as long as the resource stock has not been depleted.

The formal proof of the lemma is presented in the “Appendix”; the intuition, however, is very simple. It follows from the fact that every harvester is infinitesimally small and therefore rationally neglects the consequences of her own consumption on the evolution of the resource stock. The cost of potential depletion of the resource is therefore a purely external one. The internal net-benefit for harvester i, on the other hand, is fully described by the instantaneous net-utility function $v(c_i(t))$, which is maximised at $c_i(t)=c_\alpha$ whenever this is feasible, i.e., whenever the resource stock is positive.

3.1 Equilibrium Paths

In this subsection we characterise the consumption behaviour and the evolution of the resource stock in the unique Markov perfect Nash equilibrium. So as to give a historical flavour to our discussion, we focus on the equilibrium path starting from the initial resource stock $X(0)=K$. This enables us to arrive at various narratives of what can happen when humans enter the ecosystem.⁹

To this end, we denote by $V_i$ the individual lifetime welfare of harvester i, that is,

$$\begin{aligned} V_i=\int _0^{+\infty }v(c_i(t))e^{-\delta t}\,\mathrm{d}t. \end{aligned}$$

There are two cases to study, which we treat in the following two propositions. The proofs of the propositions are presented in the “Appendix”, where we deal with arbitrary initial values $X(0)\in [0,K]$.

Proposition 1

Suppose that $\alpha \ge \alpha ^*$ and $X(0)=K$ are satisfied. In the unique Markov perfect Nash equilibrium it holds for all $t\in \mathbb {R}_+$ and all $i\in [0,N]$ that $c_{i}(t)=c_{\alpha }$ and $V_i=v(c_\alpha )/\delta$. Furthermore, the bio-mass declines from its initial value K monotonically and asymptotically to $\bar{X}_\alpha >0$.

As has been mentioned before, the condition $\alpha \ge \alpha ^*$ assumed in Proposition 1 means that the harvesting cost is high or that the per-capita MSY is large which, in turn, is the case if the population size is small. Loosely speaking, Proposition 1 covers the situation in which the population size N is small relative to the harvesting cost $\alpha$. Whenever this condition holds, Proposition 1 tells us that the natural resource will not get extinct from its initial value $X(0)=K$ even if the harvesters act non-cooperatively (extinction can occur from small initial values $X(0)<\underline{X}_\alpha$, though; see “Appendix”).

Let us now turn to the situation where $\alpha <\alpha ^*$, i.e., where harvesting costs are small relative to the population size. The following proposition demonstrates that in this case extinction is inevitable under non-cooperative behaviour, that is, the tragedy of the commons occurs in this parametric regime.

Proposition 2

Suppose that $\alpha <\alpha ^*$ and $X(0)=K$ are satisfied and consider the unique Markov perfect Nash equilibrium. There exists a finite time $T^*$, given by

$$\begin{aligned} T^{*}= \int _{0}^{K}\frac{\,\mathrm{d}X}{Nc_\alpha -G(X)}, \end{aligned}$$

(7)

such that the resource stock is entirely depleted at time $T^*$. Furthermore, it holds for all $i\in [0,N]$ that

$$\begin{aligned} c_{i}(t)=\left\{ \begin{array}{ll} c_{\alpha } &{} \text {for all }t\in [0,T^{*}), \\ 0 &{} \text {for all }t\in (T^{*},+\infty ). \end{array} \right. \end{aligned}$$

Finally, it holds that $V_i=(1-e^{-\delta T^*})v(c_\alpha )/\delta$.

3.2 The Role of Harvesting Costs

In this subsection we further explore the influence of the harvesting cost parameter $\alpha$ on the sustainability of the unmanaged resource and on individual welfare of the harvesters. To get started we illustrate the long-run steady state resource stock as a function of $\alpha$ in Fig. 4. Note that there is a jump-discontinuity at the critical level $\alpha ^*=u'(C^*/N)$, indicating that the eventual fate of the resource switches from extinction to conservation.

Fig. 4

The long-run resource stock as a function of harvesting cost

Next let us turn to the depletion time of the resource, which is given by $T^*$ as defined in (7) in the case where $\alpha <\alpha ^*$ and which is undefined for $\alpha \ge \alpha ^*$. From the properties of $c_\alpha$ stated in (6) it follows that $T^*$ is a strictly increasing function of $\alpha$. Moreover, it is easy to see that $\lim _{\alpha \rightarrow 0}T^*=0$ and $\lim _{\alpha \rightarrow \alpha ^*}T^*=+\infty$.

Finally, let us study how individual welfare $V_i$ depends on $\alpha$. It can be shown that under the maintained assumptions $V_i$ is a continuous function of $\alpha$. By definition we have $v(c)=u(c)-\alpha c$ and $c_\alpha =\hbox {argmax}\{u(c)-\alpha c\,|\,c\in \mathbb {R}_+\}$. Together with the envelop theorem this implies that $v(c_\alpha )$ is strictly decreasing with respect to $\alpha$. In the case of high harvesting costs $\alpha \ge \alpha ^*$ we have $V_i=v(c_\alpha )/\delta$ and it follows therefore that $V_i$ is strictly decreasing in $\alpha$. The situation is more complicated for low harvesting costs $\alpha <\alpha ^*$. Since $v(c_\alpha )$ is strictly decreasing in $\alpha$ whereas $T^*$ is strictly increasing, the monotonicity behaviour of individual welfare $V_i=(1-e^{-\delta T^*})v(c_\alpha )/\delta$ with respect to $\alpha$ depends on the size of the time-preference factor $\delta$. We do not provide a complete analysis for the general case, but merely illustrate what can happen in the context of the r–K model with iso-elastic utility.

Illustration 4

Consider the r–K model with iso-elastic utility function and parameter values $K=r=N=1$ and $\beta =1/2$. Note that these parameter values imply that $\alpha ^*=2$. Figures 5 and 6 show individual welfare $V_i$ as a function of $\alpha$ for the cases where $\delta =0.1$ and $\delta =1$, respectively. The relevant formulas are presented in the “Appendix”. $\square$

Fig. 5

Individual welfare as a function of $\alpha$ for $\delta =0.1$

Fig. 6

Individual welfare as a function of $\alpha$ for $\delta =1$

Remark 1

Figures 5 and 6 show that even though $\delta$ has no influence on the equilibrium consumption trajectory in the unmanaged common, it influences the welfare evaluation of changes in the consumption trajectory that would occur if $\alpha$ or N or the ecosystem’s productivity was to change. If unit harvesting cost falls, say, from $\alpha =1.8$ to $\alpha '=1.7$, then the time to ruin for the unmanaged commons also falls. However, we can see from the figures that the welfare of the representative individual is higher under the $\alpha '$ regime (compared to the $\alpha$ regime) if $\delta =1$, and lower under the $\alpha '$ regime (compared to the $\alpha$ regime) if $\delta =0.1$. $\square$

4 Harvesting the Commons Optimally

Because the cost of verifying someone else’s harvest is positive ($\varepsilon$), no agent has a unilateral incentive to verify what others do. But if $\varepsilon$ is small, then so is $N\varepsilon$ small. It then pays consumers to cooperate and enforce the collectively optimal consumption policy. Because the problem to be studied is convex, optimum personal consumption is independent of i. That means consumption in the managed common is the solution to the following problem: Choose a consumption path $c:\mathbb {R}_+\mapsto \mathbb {R}_+$ so as to

$$\begin{aligned} \left. \begin{array}{l@{\quad }l} \text {maximize} &{} \displaystyle \int _{0}^{\infty }Nv(c(t))e^{-\delta t}\,\mathrm{d}t \\ \text {subject\ to} &{}\mathrm{d}X(t)/\mathrm{d}t=G(X(t))-Nc(t)\;\;\text {for }t\in \mathbb {R}_+, \\ &{} c(t)\ge 0\;\text {if }X(t)\ge 0;c(t)=0\;\text {if }X(t)=0, \\ &{} X(0)=K. \end{array} \right\} \end{aligned}$$

(8)

Remark 2

If we wish to conduct a welfare evaluation of a change in N, we would need to identify the zero of the function v (i.e., v would have to be unique up to positive linear transformations). For notational simplicity we have so scaled the function v that $v(0)=0$, and thus $u(0)=0$ [condition (3)]. But that means $v(c)\ge 0$ for all c in the neighbourhood of $c=0$. On the face of it, this is a weakness, because the scaling does not permit us to distinguish lives that go well from those that go badly. We should therefore identify the consumption rate $c^p>0$ that is deemed to be the poverty line, by which it is required that $v'(c^p)>0$, $v(c^p)=0$, and $v(c)<0$ for all $c\in [0,c^p)$. Meade (1955) called $c^p$ “welfare subsistence”. To be sure, under the above rescaling there would be a value of consumption, label it $c^d$, such that $v'(c^d)<0$, $v(c^d)=0$, and $v(c)<0$ for all $c>c^d>0$. But $c^d$ and consumption rates above $c^d$ would signify lives of drudgery, not poverty. As we will confirm below (Propositions 3, 4), drudgery can be, and is, avoided by an optimizing community of harvesters; but poverty cannot be avoided in the long run if N is large (Proposition 4). Under the scaling we adopted in (3), welfare evaluations of changes in N would use $v(c)-v(c^p)$ as the basis for comparisons, not v(c).$\square$

Because v is a strictly concave function and the state equation is linear in the control variable, standard results imply that the optimal control problem in (8) has a solution (see, e.g., Baum 1976). Due to the convexity assumptions imposed on the model, this solution has to be unique. The (spot) shadow price of the resource is

$$\begin{aligned} P(t)=v'(c(t)). \end{aligned}$$

As in the case of the unmanaged commons, there are two cases to consider, which we treat in two separate propositions.

Proposition 3

Suppose that $\alpha \ge \alpha ^*$ and $X(0)=K$ are satisfied. The unique optimal solution to problem (8) satisfies $c(t)=c_{\alpha }$ and $P(t)=0$ for all $t\in \mathbb {R}_+$. Furthermore, the bio-mass declines from its initial value K monotonically and asymptotically to $\bar{X}_\alpha >0$.

We do not provide a formal proof of this result, because it is well known; see e.g., Clark (2010). The intuitive explanation is as follows: Under the stated assumptions it is feasible to set $c(t)=c_{\alpha }$ for all t. Since $c_{\alpha }$ maximises v(c) over all $c\in \mathbb {R}_+$, this must be the unique optimal solution. Because there are no constraints on the choice of c(t), the resource has no social scarcity value, i.e., P(t) is equal to 0 for all t. The asymptotic convergence of the resource stock to $\bar{X}_\alpha$ follows by the same reasoning as in Proposition 1.

The optimal solution of problem (8) is most conveniently described by phase diagrams. Under the assumption $\alpha \ge \alpha ^*$ stated in Proposition 3 there are two cases to distinguish, namely whether $c_\alpha$ is large or small. More precisely, let us define $\hat{X}_\delta$ as the Golden Rule resource stock satisfying $G'(\hat{X}_\delta )=\delta$ and let $\hat{c}_\delta =G(\hat{X}_\delta )/N$ be the corresponding stationary consumption level. The phase diagram for the case $c_\alpha >\hat{c}_\delta$ is shown in Fig. 7 whereas the diagram for $c_\alpha <\hat{c}_\delta$ can be seen in Fig. 8.

Fig. 7

Phase diagram for $\alpha \ge \alpha ^*$ and $c_\alpha >\hat{c}_\delta$

Fig. 8

Phase diagram for $\alpha \ge \alpha ^*$ and $c_\alpha <\hat{c}_\delta$

The point labeled S in these figures is the Golden Rule stationary state $(\hat{X}_\delta ,\hat{c}_\delta )$. There are two more optimal stationary states in Fig. 7, namely $(\underline{X}_\alpha ,c_\alpha )$ and $(\bar{X}_\alpha ,c_\alpha )$. The result from Proposition 3 is reflected by the horizontal thick arrow starting at the right edge of the figure and leading to the stationary state $(\bar{X}_\alpha ,c_\alpha )$. The stationary state $(\underline{X}_\alpha ,c_\alpha )$ is unstable, whereas both S and $(\bar{X}_\alpha ,c_\alpha )$ are saddlepoint stable stationary states. In the case $c_\alpha <\hat{c}_\delta$, which is shown in Fig. 8, the Golden Rule stationary state S is not optimal, the stationary state $(\underline{X}_\alpha ,c_\alpha )$ is saddlepoint stable from the left, and the stationary state $(\bar{X}_\alpha ,c_\alpha )$ is saddlepoint stable (from both sides). In both of the diagrams, it is clearly seen that extinction is never optimal but that $\lim _{t\rightarrow +\infty }X(t)=\min \{\underline{X}_\alpha ,\hat{X}_\delta \}>0$ holds for all strictly positive initial resource stocks X(0).

Comparison of Propositions 1 and 3 shows that if $\alpha \ge \alpha ^*$, it is a matter of social indifference whether a common is unmanaged or managed. The resource’s social scarcity price is zero. Property rights do not matter. Note, however, that this observation holds for $X(0)=K$ but is not necessarily true for small initial values of the resource.

Remark 3

Empirical studies on fisheries have found strong evidence of the presence of stock externalities, which in the present context means that $\alpha$ is a declining function of X. Introducing such a feature into the present model would invalidate the irrelevance of property rights. Indeed, if harvesting costs are stock-dependent, a social planner with a positive time-preference rate would extract the resource stock at a slower pace than the agents in the unmanaged commons in order to exploit the low extraction cost for a longer period. In other words, the resource’s social scarcity value in the case of stock externalities would no longer be zero. $\square$

Now suppose that $\alpha <\alpha ^*$ holds. In this regime the solution to problem (8) resembles the familiar Ramsey-Cass-Koopmans trajectory, in which aggregate consumption monotonically approaches the Golden Rule stationary state $(\hat{X}_\delta ,c_\delta )$. We have the following result, which is illustrated in Fig. 9.

Proposition 4

If $\alpha <\alpha ^*$ and $X(0)=K$, the optimum harvesting policy has the following properties: (i) X(t) declines monotonically from K and converges to $\hat{X}_{\delta }\in (0,X^*)$, (ii) the harvesting rate of the representative agent, c(t), declines monotonically and converges to $\hat{c}_{\delta }$, and (iii) the shadow price of the resource at time t is positive for all $t\in \mathbb {R}_+$.

Fig. 9

Phase diagram for $\alpha <\alpha ^*$

The above proposition shows that it is not optimal from a social point of view to deplete the resource completely even if the harvesting costs are small. Instead, it is optimal to sustain a resource stock that is defined by the Golden Rule. Throughout the entire infinite time-horizon the resource has a positive shadow price, which reflects its scarcity value.

Finally, we can draw a bifurcation diagram that summarizes how the optimal stationary states change as the parameter $\alpha$ increases from 0 to $+\infty$. This bifurcation diagram is drawn in Fig. 10. The bold curves are the optimal steady states and the arrows indicate the direction of the flow of the resource stock. Note that the modified Golden Rule qualifies as an optimal stationary state only when $\alpha \le \alpha _\delta$, where $\alpha _\delta$ is that parameter value $\alpha$ for which $c_\alpha$ coincides with the Golden Rule consumption level $\hat{c}_\delta$. The stationary state $\hat{X}_\delta$ is globally asymptotically stable for $\alpha <\alpha ^*$ and locally asymptotically stable for $\alpha \in [\alpha ^*,\alpha _\delta ]$. The point $(\bar{X}_\alpha ,c_\alpha )$ is a locally asymptotically stable optimal stationary state whenever $\alpha \ge \alpha ^*$. The point $(\underline{X}_\alpha ,c_\alpha )$ is an optimal stationary state for all $\alpha \ge \alpha ^*$. It is unstable for $\alpha \in [\alpha ^*,\alpha _\delta )$, and it is one-sided asymptotically stable for $\alpha \ge \alpha _\delta$.

There is a fold bifurcation at $\alpha =\alpha ^*$, when a pair of new fixed points emerges. As the harvesting cost passes this critical value, the long-run resource stock changes discontinuously from the Golden Rule value $\hat{X}_\delta$ to the MSY-stock $X^*$ (or vice versa).

Fig. 10

Bifurcation diagram for parameter $\alpha$

Remark 4

It is instructive to check whether and how Propositions 1–4 are affected if the harvested resource is exported and the export revenue is consumed. We now need to distinguish between harvest and consumption. The simplest case to imagine is one where the economy is small, so that it faces a fixed world price $p > 0$. If Y(t) is the total quantity harvested at t, aggregate consumption is $C(t) = pY(t)$, and the representative harvester’s utility is u(pY(t) / N). The model now contains an additional parameter p. Although Propositions 1–4 maintain their general properties, the threshold values of $\alpha$ and N are now functions of p. For example, if in our new notation $Y^*$ is the maximum sustainable yield, then in the notation of Sect. 2.4, $\alpha ^* = u'(pY^*/N)$. It follows that the higher is the price p, the larger is the population N that can be sustained by the ecosystem.

Consider next the case where the economy has market power. Let p(Y) be the foreign demand schedule, where $p'(Y) < 0$. Then $C(t)=p(Y(t))Y(t)$. Assume that for all $\alpha$ there exists a value Y such that $p(Y)Y = Nc_\alpha$. The equilibrium condition in Proposition 1 now reads $u'(p(Y^*)Y^*/N) = \alpha$. Moreover, in Proposition 4 the optimum export tariff comes into play. $\square$

5 Commentary

Classifying the processes through which those among the past societies he had studied had undermined themselves by damaging their environment, Diamond (2005: p. 6) identified eight categories: (i) soil problems (erosion, salinisation, and loss of soil fertility); (ii) water management problems; (iii) effects of introduced species on native species; (iv) human population growth; (v) deforestation and habitat destruction; (vi) overhunting; (vii) overfishing; (viii) increased per capita impact of people.

The list, drawn from his absorbing and moving narratives, is revealing. But to show that in a particular human habitat a rise in per capita impact of people on their environment (category (viii)) ruined the resource base a millennium ago does not help to explain why it got ruined there; it merely describes a process of habitat destruction. In the same vein, to say that overhunting or overfishing ruined a resource base does not amount to an explanation for why and how overhunting or overfishing took place. So we distinguish categories (i)–(iv), which are factors that can trigger a breakdown of the resource base, from categories (v)–(viii), which point to human activities that degrade the environment. The analysis in this paper enables us to confirm the role played by categories (i)–(iv) on Diamond’s list, and it puts flesh into the processes that characterise categories (v)–(viii).

The mechanisms driving open-access renewable natural resources in our model are shaped by population size N, technology $\alpha$, and the commons’ productivity (in the r–K model, by r and K). We have shown that other things equal, if N is small relative to $\alpha$, open-access commons do not face destruction; they are preserved (Proposition 1). We have found, more strikingly, that the commons are harvested at the collectively optimal rate (Propositions 1 and 3). Property rights do not matter when N is small relative to $\alpha$ because resources lack a social scarcity value. However, if other things equal N is large relative to $\alpha$, open-access renewable natural resources suffer from the tragedy of the commons (Proposition 2). Freedom in the commons brings ruin to all even though it is in the collective interest to enforce a sustainable consumption policy (Propositions 2 and 4). Property rights matter when N is large relative to $\alpha$ because resources have a social scarcity price.

Propositions 1 and 3 imply that the harvesters’ time-preference $\delta$ has no influence on resource allocation if N is small relative to $\alpha$. Even more strikingly, Proposition 2 tells us that so long as $r > \delta$, myopia should not be used to explain non-sustainable resource consumption.

Given $\alpha$, the value of N at which a socio-ecological system bifurcates is an increasing function of the ecosystem’s productivity (see Sect. 2.4). A sudden crash in productivity (drought, pestilence) can tip a common into ruin. By the same token, population overshoot can tip the fate of a common toward destruction. Imagine then that a community of harvesters has experienced a population overshoot. If they are able to change course in time and convert the common into a collectively managed resource, they avoid disaster (Propositions 2 and 4 and “Appendix”). But that does not mean that the community necessarily avoids hardship. If the population overshoot is large, the optimising community faces hardship in the long run, even deep poverty, not because people exhaust their resource base, but because the resource base is unable to support them at a tolerable standard of living: the community falls below the poverty line (Remark 2, Proposition 4 and “Appendix”). The optimum consumption rate in the long run is independent of harvesting cost $\alpha$, although of course the harvesters’ well-being v(c) depends on $\alpha$. The latter fact implies that if, other things equal, harvesting cost is very high, $c_\alpha$ is less than the welfare subsistence level $c^d$ (Remark 2), in which case the society in question would experience extreme poverty no matter how well it was able to manage its resource base. Poverty in this case would not be traceable to low ecosystem productivity but to large harvesting costs. Those circumstances prevailed in the very distant past, when population was thin and technology was primitive.

Our results also speak to studies of those past societies that faced environmental stress. The question is not whether societies can be expected to take action so as to overcome environmental adversities; we should not expect people to take an impending disaster lying down. Rather, the question is whether a society is successful in fending off disaster. In a sequence of case studies, Diamond (2005) found that past societies in Highland New Guinea, Japan, Tikopia, and Tonga faced problems of deforestation, but then developed successful forest management practices and population control. He also found that, in contrast, Easter Island and Mangareva failed to develop successful forest management and collapsed as a result.

Diamond (2005) also found a common pattern in past collapses: Population growth that followed access to an abundant resource base in due course forced people to intensify the means of food production (irrigation, terracing, double-cropping) and to expand into marginal land. In effect, growing populations led to a mining of the resource base, which in turn left populations vulnerable to climatic variations. Our model speaks to that broad pattern of events. One possibility that has been explored by past societies to counter population overshoot and/or food system collapse is to look for resources elsewhere. Creating new colonies from which resources can be imported has been one way of doing that; large scale migration has been another. Barbier (2011) contains a fine historical study of the resource basis of economic development.

Proposition 2 and the “Appendix” say that collapse occurs abruptly. Abruptness is a feature to be expected of a sharp model of open access resources. In contrast Proposition 4 and the “Appendix” include cases where, in the face of a population overshoot, people try to organise their harvesting pattern so as to prevent collapse. If the overshoot is large, the proposition says that the society faces decline and will eventually experience acute poverty. But the decline can be expected to happen only gradually, even as people harvest at rates that avoid total collapse.

In a notable paper, Brander and Taylor (1998) studied a society that harvests an open-access renewable natural resource and produces a consumption good. Labour is the single input in both sectors. Population grows and falls in accordance with Malthusian principles (it grows when the standard of living is high, it declines when the standard of living is low). Competition reduces resource rents to zero at each date, akin to the theory of timeless contestable markets. In comparison to the present model, theirs is in some ways more elaborate (population is endogenous and there is a consumption goods sector, distinct from the resource sector), in others less so (people are entirely myopic and the socio-ecological dynamics evolves as a sequence of momentary equilibria of single-period optimisers). Their model contains three possible equilibria: population collapse, at $X = 0$ and $X = K$, and an intermediate value of X at which the population stabilises and the society survives. Depending on the parameters of the model, the system asymptotes to one of the equilibria. The authors’ simulations of the r–K model reveal that other things equal if r is small, the system displays periodic population overshoot. The authors relate their model to the fate of Easter Island, by noting that the species of palm in the island was especially slow-growing. As is well known, by the time Europeans first anchored there, a once advanced society had collapsed. The authors also explain the 12 mystery islands in Polynesia that had collapsed entirely by the time Europeans visited them, by observing that if K is small in their model, $N = 0$ is the only possible long run outcome.

Previously, Dasgupta (1982: Ch. 6) had studied an open-access fishery whose product could be sold in the market at a fixed price. In contrast to the model explored in this paper (Remark 4), Dasgupta assumed that the fishery was “contestable”, in that the rate of entry by fishing units into the catchment was taken to be positive if instantaneous profits are positive, but negative if instantaneous profits are negative. Harvesting cost per unit of catch was assumed to be a declining function of the fish stock and an increasing function of the number of active fishing units. The socio-ecological system thereby harboured both a stock externality and a crowding externality. Dasgupta found that the system bifurcates at a critical ratio of the market price of fish to the unit harvesting cost. He showed that if the ratio is high, the fishery is doomed; but that if the ratio is small, the fishery remains alive indefinitely. The model points to the significance of external demand for the fate of a contestable open-access common; that is, in contrast to the finding in Remark 4, where harvesters are far sighted, strong external demand is bad news for renewable natural resources in contestable markets.

Greenland Norse communities disappeared in the fifteenth century, during a period known as the Little Ice Age. Recent findings show that the communities were fishermen, and also hunters of seal and walrus tusks (Kintisch 2016). Tusks were exported to the Continent. The findings also show that the colder climate led to an increase in harvesting costs, owing to the more frequent incidence of severe storms over the sea. The economic downturn in the Continent during the Little Ice Age also led to a fall in the demand for tusks, meaning that the export price of tusks fell. Proposition 4 and Remarks 2 and 3, taken together, would say that the Norse experienced a fall in the standard of living, to below welfare subsistence. The prevailing population size proved to be unviable under the new climatic conditions.

PNAS (2012) contains a special feature on historical collapses. Contributors reported twelve studies of past societies that had faced environmental stresses. Seven were found to have suffered severe transformation, while five overcame them through changes in their practices. Butzer (2012) for example reported the ways a number of societies in fourteenth–eighteenth centuries Western Europe displayed resilience by coping with environmental stresses through innovation and agricultural intensification. Like Diamond (2005), he concluded that collapse is rarely abrupt. In a revealing study of a modern-day society, Turner and Ali (1996) showed that in the face of rising population and a deteriorating resource base, small farmers in Bangladesh have expanded production by intensifying agriculture practices (introducing multiple cropping and collectively strengthening drainage systems and flood and storm defenses). The farmers have not been able to thrive, they still live in poverty, but they have staved off collapse (they have not abandoned their villages en masse for cities), at least for now.

That collapse is rarely abrupt suggests that socio-ecological systems facing stress become less resilient in withstanding shocks and surprises. In a study of European Neolithic societies that began some 9000 years ago, Downey et al. (2016) have found that the introduction of agriculture spurred population growth, but that societies in many cases experienced demographic instability and, ultimately, collapse. Interestingly, the authors have uncovered evidence of warning signs of eventual population collapse, reflected in decreasing resilience in the socio-ecological system. In a commentary on Downey et al. (2016) and Scheffer (2016) notes that there were early warning signs, in the form of reduced resilience to small disturbances, preceding the great drought in the late 1270s that destroyed the people who had built the iconic alcove sites of Mesa Verde. In our model the early warning signs would be the heightened rate at which ecosystem services would fall in response to small declines in the resource stock.¹⁰

It is tempting to extend the socio-ecological model in our paper to cover the entire biosphere. This involves heroic aggregation, but perhaps not much more heroic than the aggregation involved in estimating global incomes and their movement through time.¹¹ As a first cut into a deep and difficult problem, we may think of the biosphere as a gigantic renewable natural resource, offering humanity ecological services.

Studying biogeochemical signatures of the past 11,000 years, Waters et al. (2016) have provided a revealing sketch of the Earth system in the present era, now named the Anthropocene. The authors noted that a sharp increase took place in the middle of the twentieth century in the rate of deterioration in the workings of Earth’s life support system. They have proposed that mid-twentieth century should be regarded as the time we entered the Anthropocene.¹²

Their reading is consistent with macroeconomic statistics. World population in 1950 was 2.5 billion. Global GDP was a bit over 5 trillion dollars (PPP). The average person in the world was poor, with an annual income of a bit over 2,000 dollars (PPP). Since then the world has prospered materially beyond recognition. World income per capita today is 15,000 dollars (PPP) and population has increased to 7.4 billion. World output of final goods and services today is about 110 trillion dollars (PPP), which help to explain not only the stresses to the Earth system that Waters et al. (2016) have drawn attention to, but they also hint at the possibility that humanity’s demand for the ecological services (in our notation C) has for some time exceeded the biosphere’s capacity (in our notation G(X)) to supply them.

To imagine the biosphere as a renewable natural resource raises a further problem. Even two thousand years ago, when global population was under 250 million and per capita income a bit over a dollar a day, it would have been a reasonable approximation to treat humanity as a separate entity from the biosphere. Today it is no longer possible to do so. We are much engaged in transforming the biosphere by both creating biomass and destroying it. So we have to imagine humanity as at once a constituent of the biosphere and an entity separate from it. No doubt that is a stretch, but it is possible to do it without running into contradictions. We can avoid contradiction by noting that a portion of G(X), say $\theta$, is needed for the maintenance of the biosphere. So, if over a period of time G(X) was to be usurped entirely by humanity, X would shrink and biodiversity would be reduced. If during an interval of time humanity was to consume even more than G(X), X would shrink even more, further drawing down biodiversity. Humanity is doing that now, which is what has led Wilson (2016) to propose that we should leave half the biosphere alone; that is, set $\theta$ equal to 0.5. The amount $(1-\theta )G(X)$ should therefore be interpreted as the useable flow of biomass; useable, that is, by humanity.¹³

In their classic paper on the impact of human activity on the biosphere, Ehrlich and Holdren (1971) pointed to technology, broadly construed, as a determining factor in the use of natural resources. Technology plays a role in Diamond’s (2005) case studies (agricultural intensification, for example), but it does not appear on his list of factors that led societies to undermine themselves. That should not be surprising, because technological improvements can hardly be thought to be bad. But technological advances that are patently good can have side-effects that are not benign. Moreover, technological advances (a lowering of $\alpha$) are irreversible. So their use has to be tempered by major institutional changes if one wants to prevent consequences that are not benign. The ability to use fossil-based energy at large scales has transformed lives for the better, but it has created the unintended consequence of global climate change. Bull-dozers and chain-saws enable people to deforest land at rates that would have been unimaginable 250 years ago, and modern fishing technology devastate large swathes of sea beds in a manner unthinkable in the past. These are but three examples of otherwise beneficial technological change. Jansson et al. (2003) point to the role irreversibility in the establishment of new management practices (the authors call the irreversibility “sunk-costs”) played in making ancient societies vulnerable to collapse. Our model speaks to that vulnerability by revealing that a decline in $\alpha$ can play havoc in open-access commons.

Appendix

Let $c_{i}(t)$ be agent i’s consumption rate at t. We consider the following game with a continuum of players $i\in [0,N]$. Player i seeks to maximise

$$\begin{aligned} \int _0^\infty v(c_i(t))e^{-\delta t}\,\mathrm{d}t \end{aligned}$$

subject to the control constraint

$$\begin{aligned} c_i(t)\left\{ \begin{array}{l@{\quad }l} \in \mathbb {R}_+&{} \text{ if } \;X(t)>0,\\ =0&{} \text{ if } \;X(t)=0.\end{array}\right. \end{aligned}$$

(9)

The state of the system evolves according to

$$\begin{aligned} \dot{X}(t)=G(X(t))-\int _0^Nc_j(t)\,\mathrm{d}j\,,\; X(0)=x, \end{aligned}$$

(10)

where $x\in [0,K]$ is a given initial state.

A Markovian strategy for harvester i (call it $\sigma _i$) determines her consumption rate as a function of the current state X(t), that is, $c_i(t)=\sigma _i(X(t))$ for all t. A Markovian strategy $\sigma _i:\mathbb {R}_+\mapsto \mathbb {R}_+$ is feasible, if $\sigma _i(0)=0$ holds. A strategy profile is a collection of feasible Markovian strategies $\{\sigma _j\,|\,j\in [0,N]\}$, one for each player, and it is called a Markov perfect Nash equilibrium if it holds for all $i\in [0,N]$ that the optimisation problem of player i when all other players $j\ne i$ use their strategies $\sigma _j$ is solved by applying the strategy $\sigma _i$.

Proof of Lemma 1

Since every harvester is infinitesimally small, she rationally disregards the influence of her harvesting rate on the evolution of the state in Eq. (10). Consequently, the feasible consumption set for every player is $\mathbb {R}_+$ as long as $X(t)>0$ holds. Together with the properties of the function v this implies that in every Nash equilibrium consisting of Markovian strategies it must hold that $c_i(t)=c_\alpha$ whenever $X(t)>0$, whereas the constraint (9) pins down $c_i(t)=0$ in case of $X(t)=0$. Taking these observations together, it follows that the only Markovian Nash equilibrium consists of a strategy profile in which every player chooses the strategy $\sigma :\mathbb {R}_+\mapsto \mathbb {R}_+$ defined by

$$\begin{aligned}\sigma (X)=\left\{ \begin{array}{cl}c_\alpha &{} \text{ if } X>0,\\ 0&{} \text{ if } X=0.\end{array}\right. \end{aligned}$$

Since the above arguments are completely independent of the initial value x, it follows that the proposed Nash equilibrium is Markov perfect.$\square$

Proofs of Propositions 1 and 2

Lemma 1 demonstrates that, in equilibrium, the resource stock evolves according to

$$\begin{aligned} \dot{X}(t)=\left\{ \begin{array}{ll}G(X(t))-Nc_\alpha &{} \text{ if } X(t)>0,\\ 0&{} \text{ otherwise. }\end{array}\right. \end{aligned}$$

(11)

Suppose first that $\alpha <\alpha ^*$, which is the case considered in Proposition 2. In this case, it holds that $\dot{X}(t)=G(X(t))-Nc_\alpha \le C^*-Nc_\alpha <0$ for all t at which X(t) is positive. This shows that there must exist $T^*$ such that $X(t)>0$ for all $t<T^*$ and $X(t)=0$ for all $t\ge T^*$. We have

$$\begin{aligned} x= & {} X(0)-X(T^*)\\= & {} -\int _0^{T^*}\dot{X}(t)\,\mathrm{d}t\\= & {} \int _0^{T^*}Nc_\alpha \,\mathrm{d}t-\int _0^{T^*}G(X(t))\,\mathrm{d}t\\= & {} Nc_\alpha T^*+\int _0^xG(X)/[G(X)-Nc_\alpha ]\,\mathrm{d}X. \end{aligned}$$

Rearranging this equation, we obtain

$$\begin{aligned}T^*=\frac{1}{Nc_\alpha }\int _0^x\left\{ 1-\frac{G(X)}{G(X)-Nc_\alpha }\right\} \,\mathrm{d}X=\int _0^x\frac{\,\mathrm{d}X}{Nc_\alpha -G(X)},\end{aligned}$$

which proves (7). The statement about $V_i$ is obviously true.

Now consider the case $\alpha \ge \alpha ^*$. It follows easily from the equilibrium law of motion (11) that

$$\begin{aligned}\lim _{t\rightarrow +\infty }X(t)=\left\{ \begin{array}{cl}\bar{X}_{\alpha }&{} \text{ if } x\in (\underline{X}_\alpha ,K],\\ \underline{X}_\alpha &{} \text{ if } x=\underline{X}_\alpha ,\\ 0&{} \text{ if } x<\underline{X}_\alpha .\end{array}\right. \end{aligned}$$

Proposition 1 follows as the special case $x=K$.$\square$

The formulas underlying Figs. 5and6 Consider the r–K model. If $\alpha <\alpha ^*$, then it holds that $Nc_\alpha >C^*=rK/4$. Hence, defining

$$\begin{aligned} B_\alpha =4Nc_\alpha -rK \end{aligned}$$

it follows that $B_\alpha >0$ when $\alpha <\alpha ^*$. As long as $X(t)>0$, the resource stock evolves according to

$$\begin{aligned} \dot{X}(t)=rX(t)\left[ 1-\frac{X(t)}{K}\right] -Nc_\alpha \,,\;X(0)=x. \end{aligned}$$

It is straightforward to verify that the function

$$\begin{aligned} X(t)=\frac{K}{2}-\sqrt{\frac{KB_\alpha }{4r}}\tan \left\{ t\sqrt{\frac{B_\alpha r}{4K}}+\arctan \left[ \sqrt{\frac{r}{B_\alpha K}}(K-2x)\right] \right\} \end{aligned}$$

is the unique solution of the above initial value problem. The extinction time $T^*$ can be obtained by solving $X(T^*)=0$, which yields

$$\begin{aligned} T^*=\sqrt{\frac{4K}{B_\alpha r}}\left\{ \arctan \left( \sqrt{\frac{Kr}{B_\alpha }}\right) +\arctan \left[ \sqrt{\frac{r}{B_\alpha K}}(2x-K)\right] \right\} . \end{aligned}$$