Firms’ Emissions and Self-Reporting Under Competitive Audit Mechanisms

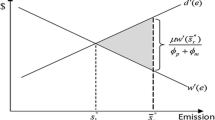
Abstract

Many environmental tax systems rely on self-reported emissions by firms. These emission reports are verified through costly auditing efforts by regulatory agencies that are constrained in their auditing budgets. A typical assumption in the literature is that the agencies allocate audit efforts randomly among otherwise identical firms (random audit mechanism). This paper compares the incentives on firms’ emissions and self-reporting behavior under the random audit mechanism to the incentives under competitive audit mechanisms (CAMs). Under CAMs, higher reported emissions by a firm relative to other firms result in a lower audit intensity. This creates a reporting contest between the firms. The two CAMs under investigation apply different degrees of competitiveness in the reporting contest. I find that both CAMs lead to more truthful reporting, which is in line with the previous literature. Interestingly and novel to the literature, I find that some competition in reporting may induce fewer emissions compared with random auditing, while too much competition in reporting may induce comparatively higher emissions caused by firms.

Appendix

1.1 Best Responses for the Reporting Stage 2

This section states and derives the complete best response function of firm 1 (BR1) at the reporting stage 2 of the game under the Tullock audit mechanism. If the funding level of the agency is such that $B\in (0,1]$, the BR1 is defined as:

$$\begin{aligned} r_{1}(e_{1},r_{2},B)=\left\{ \begin{array}{ll} \varepsilon &{}\quad \hbox {if }\quad r_{2}=0\\ \sqrt{Br_{2}(r_{2}+e_{1})}-r_{2} &{}\quad \hbox {if }\quad r_{2}\le e_{1}\frac{B}{1-B}\\ 0 &{}\quad \hbox {if }\quad r_{2}>e_{1}\frac{B}{1-B} \end{array} \right. \end{aligned}$$

(18)

where $\varepsilon$ is the smallest possible reporting unit. If $B=1$, the BR1 is defined as: $r_{1}(e_{1},r_{2},1)=\sqrt{r_{2}(r_{2}+e_{1})}-r_{2}$, i.e. for large $r_{2}$ the BR1 converges to a parallel line somewhere between $r_{1}=0$ and $r_{1}=e_{1}.$ If $B\in (1,2)$, the BR1 is defined as:

$$\begin{aligned} r_{1}(e_{1},r_{2},B)=\left\{ \begin{array}{ll} \varepsilon &{}\quad \hbox {if }\quad r_{2}=0\\ r_{2}\frac{1}{B-1} &{}\quad \hbox {if }\quad 0<r_{2}\le e_{1}\frac{(B-1)^{2}}{B-(B-1)^{2} }\\ \sqrt{Br_{2}(r_{2}+e_{1})}-r_{2} &{}\quad \hbox {if }\quad e_{1}\frac{(B-1)^{2}}{B-(B-1)^{2}}<r_{2}<e_{1}\frac{1}{B-1}\\ e_{1} &{}\quad \hbox {if }\quad e_{1}\frac{1}{B-1}\le r_{2} \end{array} \right. \end{aligned}$$

(19)

1.1.1 Derivation of the BR1

We note, that the FOC, $\frac{\partial E\Pi _{1}}{\partial r_{1}}=0$, of the maximization problem in (4) is:

$$\begin{aligned} -1+\displaystyle \frac{r_{2}}{(r_{1}+r_{2})^{2}}B(e_{1}-r_{1} )+\displaystyle \frac{r_{2}}{r_{1}+r_{2}}B=0. \end{aligned}$$

(20)

The assumption that the tax is low enough to guarantee positive profits under full-compliance, i.e. $g_{i}(e_{i}^{fc})-te_{i}^{fc}>0$, eliminates the possibility of the case that $e_{i}=0$ for $i=1,2.$

Thus, $e_{1}>0.$ If $e_{1}>0$ and $r_{2}=0$ then the best response of firm $1$ is $\varepsilon$. All remaining cases have $e_{1}>0,$ and $r_{2}>0.$

I derive (18) first, i.e. the BR1 when the audit budget is such that $B\in (0,1].$ Evaluating the first derivative (20) at $r_{1}=0$ is proportional to $(r_{2}+e_{1})B-r_{2}.$ Hence, if $(r_{2}+e_{1})B-r_{2} <0$ (or $r_{2}>e_{1}\frac{B}{1-B})$ then it is optimal to choose $r_{1}=0.$

Evaluating the first derivative (20) at $r_{1}=e_{1}$ leads to $r_{2}B-e_{1}-r_{2}.$ If $B\le 1$ then this expressions is always less than zero and the inequality $r_{2}B-e_{1}-r_{2}>0$ never holds, i.e. $r_{1} =e_{1}$ can never be optimal if $B\le 1,$ regardless of $r_{2}.$ In all other cases, the optimal reporting choice is interior, i.e. $0<r_{1}<e_{1}$ and the FOC (20) can be rearranged to $r_{1}=\sqrt{r_{2}(r_{2}+e_{1})B} -r_{2}.$

I derive (19) next, i.e. the BR1 when the audit budget is such that $B>1.$ Firm 1’s problem is to chose some $r_{1}\in [0,e_{1}]$ to maximize:

$$\begin{aligned} E\Pi _{1}=\left\{ \begin{array} [c]{llc} g(e_{1})-tr_{1}-\alpha \underline{p}\theta (e_{1}-r_{1}) &{}\quad \hbox {if }\quad \frac{r_{2}}{r_{1}+r_{2}}\le \underline{p} \hbox { (large }r_{1}\hbox {)} &{} \hbox {(i)}\\ g(e_{1})-tr_{1}-\alpha \frac{r_{2}}{r_{1}+r_{2}}\theta (e_{1}-r_{1}) &{}\quad \hbox {if }\quad \frac{r_{2}}{r_{1}+r_{2}}\in (\underline{p},\overline{p})\hbox { (intermediate }r_{1}\hbox {)} &{} \hbox {(ii)}\\ g(e_{1})-tr_{1}-\alpha \overline{p}\theta (e_{1}-r_{1}) &{}\quad \hbox {if }\quad \overline{p}\le \frac{r_{2}}{r_{1}+r_{2}}\hbox { (small }r_{1}\hbox {)} &{} \hbox {(iii)} \end{array} \right. \end{aligned}$$

We analyze each of the three cases (i)–(iii):

• Case (i): The first case, $\frac{r_{2}}{r_{1}+r_{2}}\le \underline{p},$ applies whenever $r_{1}\ge \frac{1-\underline{p}}{\underline{p}}r_{2}.$ With $B>1,$ I have $\alpha \theta >t\$which means that $\underline{p}=\max \{0,1-\frac{t}{\alpha \theta }\}=\frac{\alpha \theta -t}{\alpha \theta }$ and so $r_{1}>\frac{1-\underline{p}}{\underline{p}}r_{2}=\frac{1}{B-1}r_{2}.$ In order for this case to exist I need to assume that $e_{1}>r_{1}>\frac{1}{B-1}r_{2}.$ On this range, profit $E\Pi _{1}=g(e_{1})-tr_{1}-(\alpha \theta -t)(e_{1}-r_{1})$ is decreasing in $r_{1},$ i.e.: $\frac{\partial E\Pi _{1}}{\partial r_{1}}=\alpha \theta -2t<0,$ for $B\in (1,2).$ Hence, it can never be optimal to report some $r_{1}>\frac{1}{B-1}r_{2}.$

• Case (ii): The first derivative (20) evaluated at $r_{1}=e_{1}$ is proportional to $r_{2}(B-1)-e_{1}.$ In order for this case to exist, I need to assume that $r_{1}=e_{1}$ is feasible, i.e. that $\frac{r_{2}}{e_{1}+r_{2}}\in [\underline{p},\overline{p}].$ We can see that there is at most one stationary point. So if $r_{2}(B-1)-e_{1}\ge 0$ (or $r_{2} \ge \frac{e_{1}}{B-1}$) then $r_{1}=e_{1}$ is optimal. Note, if $r_{2} \ge \frac{e_{1}}{B-1}$ then $\frac{1}{B-1}r_{2}\ge \frac{e_{1}}{(B-1)^{2} }>e_{1}\ge r_{1}$, and so the boundary defined in case (i) is never crossed.Next I investigate the boundary where $r_{1}=\frac{1}{B-1}r_{2}.$ The first derivative (20) is proportional to $-(r_{1}-r_{2})^{2}+r_{2}B(e_{1}+r_{2})=0.$ At the point where $r_{1}=\frac{1}{B-1}r_{2}$ (which is finite) the derivative is positive whenever $e_{1}$ is sufficiently large in comparison to $r_{2},$ i.e.: $-(\frac{1}{B-1} r_{2}-r_{2})^{2}+r_{2}B(e_{1}+r_{2})>0,$ if $e_{1}$ is large in comparison to $r_{2}$. Solving for $r_{2}$ gives $r_{2}<e_{1}\frac{(B-1)^{2}}{B-(B-1)^{2}} .$ In this case, profit is increasing in $r_{1}$ when $r_{1}$ is to the left of $\frac{1}{B-1}r_{2}$ and decreasing when $r_{1}$ is to the right of this point. Hence, I conclude that $r_{1}=\frac{1}{B-1}r_{2}$ when $r_{2} <e_{1}\frac{(B-1)^{2}}{B-(B-1)^{2}}.$I need to assure that $e_{1}>\frac{1}{B-1}r_{2}$ or $r_{2}<e_{1}(B-1).$ But for $B\in (1,2)$, I have $(B-1)>\frac{(B-1)^{2}}{B-(B-1)^{2}}.$ So if $r_{2}<e_{1}\frac{(B-1)^{2} }{B-(B-1)^{2}},$ then it is automatically the case that $r_{2}<e_{1}(B-1)$ or $e_{1}>\frac{1}{B-1}r_{2}.$ Note further that if $r_{2}=e_{1}\frac{(B-1)^{2} }{B-(B-1)^{2}}$ then $\frac{1}{B-1}r_{2}=\frac{1}{B-1}(e_{1}\frac{(B-1)^{2} }{B-(B-1)^{2}})=-\frac{B-1}{B^{2}-3B+1}e_{1}\in (0,e_{1})$ for $B\in (1,2).$ Finally, the reaction $r_{1}=\sqrt{r_{2}(r_{2}+e_{1})B}-r_{2}$ is optimal if $e_{1}\frac{(B-1)^{2}}{B-(B-1)^{2}}<r_{2}<e_{1}\frac{1}{B-1}.$

• Case (iii): The third case, $\overline{p}<\frac{r_{2}}{r_{1}+r_{2}},$ applies whenever $r_{1}<\frac{1-\overline{p}}{\overline{p}}r_{2}.$ With $B>1,$ I have $\alpha \theta >t\$which means that $\overline{p}=\min \{\frac{t}{\alpha \theta },1\}=\frac{t}{\alpha \theta }$ and so $r_{1}<(B-1)r_{2}$ (or $\frac{r_{1}}{(B-1)}<r_{2})$. On this range, profit is always equal to $E\Pi _{1}=g(e_{1})-te_{1}$ regardless of the report ($0\le r_{1}\le e_{1}$). Hence, any report equal or below $e_{1}$ is a best response – in particular, $r_{1}=e_{1}$ is a best response. And so $e_{1}\$is a best response whenever $\frac{e_{1}}{B-1}<r_{2}.$I continue to assume that the firm chooses $r_{1}=e_{1}$ in case it is indifferent between any $r_{1} \in [0,e_{1}],$ such as in the present case (iii). While this assumption simplifies the analysis, it does not influence the emission choice of the firms in equilibrium. Referring to Fig. 2, the BRs only intersect once at exactly the same point with or without this assumption. Without this assumption, BR1 becomes a correspondence whenever it crosses the straight line with slope $\frac{1}{B-1}.$ To the right of this crossing point, all BR1s are below the straight line; hence, BR1 and BR2 (which is always on or above the straight line) intersect only once at exactly the same point, with or without this assumption.

This concludes the derivation of the BR1. The best response function of firm 2 can be found equivalently.

1.2 Partial Derivatives of the Reporting Equilibrium

1.2.1 For the Case $p_{i}\in (\underline{p},\overline{p})$

In order to solve the emissions equilibrium at stage 1 of the game, I require the value of the partial derivative of $r_{2}^{*}(e_{1},e_{2},B)$ with respect to $e_{1}$. I find this value near equilibrium ($p_{i}\in (\underline{p},\overline{p})$) by applying the implicit function theorem to the system of best responses, which can be written as:

$$\begin{aligned} \begin{array}{ll} (r_{2}^{*2}+r_{2}^{*}e_{1})-\frac{1}{B}(r_{1}^{*}+r_{2}^{*} )^{2}=0,\quad \hbox { and}\quad&(r_{1}^{*2}+r_{1}^{*}e_{2})-\frac{1}{B} (r_{1}^{*}+r_{2}^{*})^{2}=0 \end{array} \end{aligned}$$

(21)

The total differentiation of system (21) leads to the following matrix:

$$\begin{aligned} \left[ \begin{array}{ll} -2\frac{1}{B}(r_{1}^{*}+r_{2}^{*}) &{}\quad 2r_{2}^{*}(1-\frac{1}{B} )+e_{1}-2\frac{1}{B}r_{1}^{*}\\ 2r_{1}^{*}(1-\frac{1}{B})+e_{2}-2\frac{1}{B}r_{2}^{*} &{}\quad -2\frac{1}{B}(r_{1}^{*}+r_{2}^{*}) \end{array} \right] \left( \begin{array}{l} dr_{1}\\ dr_{2} \end{array} \right) =\left[ \begin{array}{ll} -r_{2}^{*} &{} 0\\ 0 &{} -r_{1}^{*} \end{array} \right] \left( \begin{array}{l} de_{1}\\ de_{2} \end{array} \right) \end{aligned}$$

(22)

It is required that the matrix on the left hand side of system (22) has to be non-singular, i.e. the determinant $|D|$ of this matrix is different from zero, which is shown below. The value of $|D|$ is given by:

$$\begin{aligned} |D|=4\left( \frac{1}{B}\right) ^{2}\left( r_{1}^{*}+r_{2}^{*}\right) ^{2} -\left[ 2r_{2}^{*}(1-\frac{1}{B})+e_{1}-2\frac{1}{B}r_{1}^{*}\right] \left[ 2r_{1}^{*}(1-\frac{1}{B})+e_{2}-2\frac{1}{B}r_{2}^{*}\right] >0 \end{aligned}$$

(23)

Applying Cramer’s rule to the matrix system in (22) leads to the partial derivatives of interest:

$$\begin{aligned} \displaystyle \frac{\partial r_{1}^{*}}{\partial e_{1}}&= \displaystyle \frac{2\frac{1}{B}r_{2}^{*}\left( r_{1}^{*}+r_{2}^{*}\right) }{|D|},\end{aligned}$$

(24)

$$\begin{aligned} \displaystyle \frac{\partial r_{2}^{*}}{\partial e_{1}}&= \displaystyle \frac{r_{2}^{*}\left[ 2r_{1}^{*}\left( 1-\frac{1}{B}\right) +e_{2}-2\frac{1}{B}r_{2}^{*} \right] }{|D|}. \end{aligned}$$

(25)

1.2.2 For the Case $p_{i}\notin (\underline{p} ,\overline{p})$

For future reference, I state the matrix of partial derivatives of the reporting equilibrium w.r.t. changes in $e_{1},$ for all three cases of $p_{i}:$

(26)

1.3 Single Crossing Property of the Best Response Functions

I show next, that the BRs only cross exactly once for $B\in (0,2)$ and for any $e_{i}\in (0,E]$ for $i=1,2$. Hence, the reporting equilibrium is unique.

In case $p_{i}\in (\underline{p},\overline{p}),$ $r_{1}(e_{1},r_{2} ,B)=\sqrt{Br_{2}(r_{2}+e_{1})}-r_{2}$

. The first and second derivatives of this part of the BR1 with respect to the report of firm 2 are:

$$\begin{aligned} \displaystyle \frac{\partial r_{1}(e_{1},r_{2},B)}{\partial r_{2}}&=\displaystyle \frac{\sqrt{B}(e_{1}+2r_{2})}{2\sqrt{r_{2}\left( e_{1} +r_{2}\right) }}-1=\displaystyle \frac{\sqrt{4Be_{1}r_{2}+4Br_{2}^{2} +Be_{1}^{2}}-\sqrt{4e_{1}r_{2}+4r_{2}^{2}}}{2\sqrt{r_{2}\left( e_{1} +r_{2}\right) }}\end{aligned}$$

(27)

$$\begin{aligned} \displaystyle \frac{\partial ^{2}r_{1}(e_{1},r_{2},B)}{\partial ^{2}r_{2}}&=\displaystyle -\frac{\sqrt{B}e_{1}^{2}}{4\left( r_{2}\left( e_{1} +r_{2}\right) \right) ^{\frac{3}{2}}}<0 \end{aligned}$$

(28)

From expressions (27), (28) and the complete BR1 stated in (18) and (19) above, I can derive the following properties about the shape of the BR1:

• (1) For small values of $r_{2},$ the BR1 is always above the $45^{\circ }$ line. This is because, if $B\in (0,1],$ then the derivative$\ \frac{\partial r_{1}(e_{1},r_{2},B)}{\partial r_{2}}$ is very large which can be seen from (27). If $B\in (1,2)$, then $p_{1}=\overline{p},$ and $p_{2}=\underline{p}$, and the derivative $\frac{\partial r_{1}(e_{1} ,r_{2},B)}{\partial r_{2}}$ takes on value $\frac{1}{B-1},$ which is larger than $1.$

• (2) For large $r_{2},$ the BR1 is below the $45^{\circ }$ line. This is because, if $B\in (0,1],$ the BR1 becomes negative-sloping or flat. If $B\in (1,2)$, the BR1 becomes flat at $r_{1}=e_{1}.$ Note, that the negative-sloping part of the BR1 cannot be smaller than $-1,$ i.e. $\frac{\partial r_{1}(e_{1},r_{2},B)}{\partial r_{2}}>-1.$ This can be seen from (27), because $\frac{\sqrt{B}(e_{1}+2r_{2})}{2\sqrt{r_{2}\left( e_{1}+r_{2}\right) }}>0$.

• (3) We can learn from the negative second derivative in (28) that the BR1 is concave in case $p_{i}\in (\underline{p},\overline{p}).$ If $p_{i}\notin (\underline{p},\overline{p})$ the BR1 are straight lines. In fact, the best responses are concave whenever they are strictly positive.

Concluding, the BR1 is initially above the $45^{\circ }$ line, and then crosses it once from above, for all $B\in (0,2).$ It is evident from the discussion thus far, that the BRs only cross exactly once for $B\in (0,2)$ and for any $e_{i}\in (0,E]$ for $i=1,2$.

1.4 Sufficient Condition for the Existence of $e^{t}$ as Symmetric SPNE

This section works out a sufficient condition for the existence of $e^{t}$ defined in (11) as a symmetric SPNE in pure strategies. This sufficient condition guarantees that $e_{1}=e_{2}=e^{t}$ is the only stationary point. It is also shown that $e_{1}=e_{2}=e^{t}$ is a local maximum. If $e_{1} =e_{2}=e^{t}$ is a local maximum and in addition it is the only stationary point, it follows that it has to be a global maximum.

I begin by fixing the emission level of firm 2 at the equilibrium candidate identified in Eq. (11), i.e. $e_{2}=e^{t}$ and rewrite the FOC (10) as:

$$\begin{aligned} L(e_{1})=R(e_{1},e^{t}), \end{aligned}$$

(29)

where:

$$\begin{aligned} L(e_{1})&=\frac{1}{\alpha \theta }g^{\prime }(e_{1})\end{aligned}$$

(30)

$$\begin{aligned} R(e_{1},e^{t})&=\frac{\frac{\partial r_{2}^{*}}{\partial e_{1}} r_{1}^{*}\left( e_{1}-r_{1}^{*}\right) r_{1}^{*}r_{2}^{*}+r_{2}^{*2}}{\left( r_{1}^{*}+r_{2}^{*}\right) ^{2}} \end{aligned}$$

(31)

Expression $L(e_{1})$ represents the marginal benefit associated with causing emissions and $R(e_{1},e^{t})$ represents the marginal cost of causing emissions (both are divided by constant $\alpha \theta$). Whenever $L(e_{1})=R(e_{1},e^{t}),$ the FOC holds and indicates a stationary point. Whenever $L(e_{1})$ intersects $R(e_{1},e^{t})$ from above in a diagram with $e_{1}$ on the horizontal axis, a local maximum is identified.

Figures 5 and 6 illustrate the value of $L(e_{1})$ and$\ R(e_{1},e^{t})$ for the cases $B\in (0,1]$ and $B\in (1,2)$ respectively. Specifically, the figures show the value of $L(e_{1} )$ and$\ R(e_{1},e^{t}),$ when the emissions of firm 2 are fixed at the emission level of the equilibrium candidate ($e_{2}=e^{t})$ and the emissions of firm 1, $e_{1}$ vary from $0$ to $E$ on the horizontal axis. It is straight forward to see that $L(e_{1})$ is decreasing in $e_{1}$, taking on value zero at $e_{1}=E.$ In the following, I discuss the value of $R(e_{1},e^{t})$ in both figures.

Fig. 5

$L(e_{1})$ and $R(e_{1},e^{t}):$ LHS and RHS of the FOC defined in (29) with $e_{2}$ fixed at the equilibrium candidate identified in (11), i.e. $e_{2}=e^{t}$ and $e_{1}$ varying from $0$ to $E$ when $B\in (1,2)$. Note, it is $\frac{1}{B}>\frac{8+B-B^{2}}{16-B^{2}}>\frac{B-1}{B}$ for $B\in (1,2)$

Fig. 6

$L(e_{1})$ and $R(e_{1},e^{t})$: LHS and RHS of the FOC defined in (29) with $e_{2}$ fixed at the equilibrium candidate identified in (11), i.e. $e_{2}=e^{t}$ and $e_{1}$ varying from $0$ to $E$ when $B\le 1$

If the level of underfunding is such that $B\in (1,2)$ as in Fig. 5, the graph can be partitioned into three scenarios with $k_{1}$ and $k_{2}$ as levels of emission of firm 1 as dividing points. The pair of emission levels $(e_{1},e_{2})=(k_{1},e^{t})$ leads to truthful reporting for firm 1 at stage 2 of the game; correspondingly, the pair $(k_{2},e^{t} )$ leads to truthful reporting for firm 2 at stage 2 of the game. Variables $k_{1}$ and $k_{2}$ are implicitly defined by:

$$\begin{aligned} k_{1}&:t=\alpha \theta \frac{r_{2}^{*}\left( k_{1},e^{t}\right) }{r_{1}^{*}\left( k_{1},e^{t}\right) +r_{2}^{*}\left( k_{1},e^{t}\right) }\end{aligned}$$

(32)

$$\begin{aligned} k_{2}&:t=\alpha \theta \frac{r_{1}^{*}\left( k_{2},e^{t}\right) }{r_{1}^{*}\left( k_{2},e^{t}\right) +r_{2}^{*}\left( k_{2},e^{t}\right) } \end{aligned}$$

(33)

Next, I discuss the convex downward-sloping shape of $R(e_{1},e^{t})$ in Figs. 5 and 6 for interior reporting choices, i.e. $(k_{1}<e_{1}<k_{2})$. First it is important to state that $R(e_{1} ,e^{t})$ is independent of the functional form of the benefit function, $g(e)$. The value of $R(e_{1},e^{t})$ is solely determined by $e_{1},$ $e_{2},$  $r_{1}, r_{2},$ and $B.$ Second, the best reporting responses for firm 1 in (5) and for firm 2 can be combined to the following equation:

$$\begin{aligned} r_{2}(r_{2}+e_{1})=r_{1}(r_{1}+e_{2}) \end{aligned}$$

(34)

From Eq. (34), we can see that multiplying both $e_{1}$ and $e_{2}$ by some constant, say $p$ to $pe_{1}$ and $pe_{2}$ results in the reporting choices to increase by exactly factor $p$ as well to $pr_{1}$ and $pr_{2}.$ From Eqs. (24) and (25), we can learn that the partial derivatives do not change if evaluated at $pe_{1}$, $pe_{2},$ and$\ pr_{1}$ and $pr_{2}.$ Now it is straight forward to see that the value of $R(e_{1},e^{t})$ does not change either subsequent to this change in emissions and reporting. Hence, $R(e_{1},e^{t})$ is homogenous of degree zero (HOD zero) to equal changes in $e_{1}$ and $e_{2}.$ Third, if I fix $e_{2}$ at any level of emissions and let $e_{1}$ vary from $0$ to $E$, the shape of $R(e_{1},e^{t})$ on the interval $e\in (k_{1},\min \{k_{2},E\})$ is revealed in its general form, because $R(e_{1},e^{t})$ is HOD zero. In the example illustrated in Fig. 7 I fixed the emission level of firm 2 at the equilibrium candidate, i.e. $e_{2}=e^{t}.$ This example reveals the convex downward-sloping shape of $R(e_{1},e^{t})$ in Figs. 5 and 6.

With the help of the partial derivatives of the reporting equilibrium stated in (26), I can find the values for $R(e_{1},e^{t})$ to conclude Figs. 5 and 6:

• $R(0,e^{t})=1,$   for   $B\in (0,1]$

• $R(e_{1},e^{t})\Big |_{e_{1}\le k_{1}}=1/B,$   for   $B\in (1,2)$

• $R(e_{1},e^{t})\Big |_{e_{1}\ge k_{2}}=\frac{B-1}{B},$   for   $B\in (1,2).$

Whenever $L(e_{1})$ intersects $R(e_{1},e^{t})$ from above, a local maximum is identified. Whenever this local maximum is the only stationary point, it has to be a global maximum. A sufficient condition that guarantees that $L(e_{1})$ intersects $R(e_{1},e^{t})$ uniquely from above as illustrated in Figs. 5 and 6 is stated next:

Fig. 7

Value of $L(e_{1})$ and $R(e_{1},e^{t})$ as defined in (30) and (31) for various funding levels of $B,$ with $B=(\alpha \theta )/t$. The emission level of firm 2 $e_{2}$ is fixed at the emission level of the equilibrium candidate $e^{t}$, defined in (11). The example was generated with the benefit function:$\ g(e)=e^{0.5}-e$

Sufficient condition for the existence of $(e^{t},e^{t})$ as symmetric pure strategy SPNE: There exists some $m>0$ such that if $|g^{\prime \prime }(e_{1})|>m$ for all $e\in [\max \{0,k_{1}\},\min \{k_{2},E\}],$ then a symmetric pure strategy SPNE exists.

Put differently, if $g^{\prime }(e_{1})$ is steep enough on the interval $[\max \{0,k_{1}\},\min \{k_{2},E\}],$ then it is guaranteed that the symmetric SPNE in pure strategies exists.