Abstract
The conventional economic argument favors the use of market-based instruments over ‘command-and-control’ regulation. This viewpoint, however, is often limited in the description and characteristics of the latter; namely, environmental standards are often portrayed as lacking structured abatement incentives. Yet contemporary forms of command-and-control regulation, such as standards stipulated via benchmarking, have the potential to be efficient. We provide a first formal analysis of environmental standards based on performance benchmarks. We show that under specific conditions, standards can provide efficient incentives to improve environmental performance.
Similar content being viewed by others
Notes
Despite significant advances in the use (and understanding) of market-based instruments over the last five decades, command-and-control regulation remains dominant. Explanations for instrument choice can be seen in, for example, Buchanan and Tullock (1975), Oates et al. (1989), and Aidt and Dutta (2004).
A notable exception is Montero (2002), who finds that standards may offer greater R&D incentives than permits because R&D under standards only reduces a firm’s own cost, but not that of its rivals.
Of course, the standard could also be determined by the best available technology or some other benchmark. For example, the EU has recently adopted a benchmarking mechanism to determine free allocation of EU emission allowances (EUAs) under the EU ETS where the benchmark is set to reflect the average performance of the 10 % most efficient producers in a given sector (European Commission 2011). While our theoretical model hinges on the benchmark being defined by the industry’s average performance, we are able to show that such instruments can ensure strong incentives to abate pollution.
Related studies on the political economy of environmental regulation have analyzed both how environmental policy is determined via interest groups (e.g., Heyes 1997; Aidt and Dutta 2004; Aidt 2010) as well as the creation of rents from the environmental regulation and the welfare losses incurred from rent-seeking activity (e.g., Dijkstra 1998; Malueg and Yates 2006; MacKenzie and Ohndorf 2012a).
A number of alternative interpretations are possible. For example, \(P\) could reflect a prize fund that is to be allocated to firms for their relative abatement of pollution (see the discussion section of current policies in Sect. 6). Additionally, given appropriate function specifications, our framework could be extended to a case where \(P\) would be endogenously determined by abatement efforts (see, Chung 1996), in which case such a model framework could resemble, for example, a tax-and-refund scheme.
While in a concentrated industry incentives for collusion may exist, yardstick competition can be designed to minimize these incentives, e.g., by imposing restrictions on firms admissible choices (Shleifer 1985). Therefore, we only consider non-cooperative behavior.
Note that a tax/subsidy scheme could provide equivalent incentives. Given our focus on command-and-control regulation and the fact that such policy would be significantly more complicated than a conventional emission tax, this is not considered here.
The restriction to the two-firm case is purely for ease of representation. As shown in the Appendix, our results extend to the case of \(n>2\).
When interpreted as a production license (an assumption we relax in Sect. 6), the natural application of the proposed instrument would be the regulation of the production of a homogeneous good. In these circumstances, it seems plausible to assume that producers have similar production costs and, therefore, earn the same mark-up per unit sold. Multiplied with a given demand for the good (or a legally restricted quantity of the output), this mark-up defines the producer surplus, which we hence assume to be constant and exogenous. We relax the first assumption in Sect. 4.
It is easy to verify that the second-order condition is fulfilled and \(\frac{\partial ^2 \pi _i}{\partial c_i^2} < 0\).
It is straightforward to show that any level of abatement is achieved at a lower total cost when the regulatory instrument is a standard established via benchmarking rather than a conventional command-and-control policy.
Note that we do not consider technological spillovers. If they existed in our model, we would expect investment to decrease as spillover effects would reduce the competitive advantage one could gain by investing in a more efficient technology.
Note that the regulator does not prescribe the use of any specified technology, such as in a regime where best available control technologies (BACT) are used.
Alternatively, to yield the first-best level of abatement, the regulator could simply limit the scope of aggregate operating licenses and thus the rent \(P\).
Obviously, if the tax was truly Pigouvian (i.e., first-best efficient), increased abatement would be undesirable and benchmarking could lead to abatement beyond the socially optimal; however, this would be the standard textbook comparison of an optimal instrument with a much more restrictive policy. On the other hand, it can be argued that environmental taxes are typically well below their Pigouvian levels (e.g. Ciocirlan and Yandle (2003)), which motivates our comparison of two suboptimal regulatory policies.
Rent-seeking efforts are typically viewed as being welfare decreasing. Nevertheless, the second choice variable, \(s_i\), can more generally be interpreted as effort, which could have either positive or negative welfare implications. Yet we show that even if the second instrument is welfare decreasing, its use can still improve welfare overall.
One could think of the regulator having the power to choose \(\alpha \), in which case \(\alpha \) would express the regulators valuation of abatement and rent seeking, respectively. Alternatively, one could view \(\alpha \) as being exogenous and simply show that \(\alpha < 1\) can increase the efficiency of the mechanism. We take the latter approach.
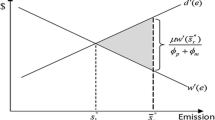
Note that \(\hat{S}\) only accounts for the direct monetary cost of rent seeking. If there were additional welfare costs related to rent seeking, of course, the range for which the latter has the potential to increase welfare would be reduced.
Note that this follows from the second-best argument that two distortionary factors may achieve an outcome closer to the first-best outcome.
Of course, regulation would not be needed, thus the proposed mechanism would not actually be employed.
It is easy to show that the results extend to the case with investment.
If benchmarking regulation is to allocate production licenses, the assumption of homogeneity on the output market is crucial.
Note, however, that market instruments may also incentivize large abatement projects that could cause similar problems if exogenous shocks occurred. Under any instrument there could then be an incentive to renegotiate the regulatory burden. As benchmarking regulation is based on individual contracts between firms and the regulator, it might be more prone to renegotiation than universal policies.
As is standard in the analysis of environmental regulation, \(a_i\) is defined as the difference between emissions from production under a baseline scenario and a scenario in which firm \(i\) takes measures to abate its pollution. While this is typically measured per firm, the interpretation of \(a_i\) as abatement per unit of production is equally possible.
An extensive description of possible measurement methods is given in Commission Regulation (EU) No. 601/2012.
With market instruments, the marginal benefit of over-reporting of abatement is constant and equal to the tax rate or permit price. Under benchmarking regulation, on the other hand, the incentive to over-state abatement is decreasing because the market share is concave in reported emissions. As a result, any positive level of monitoring achieves a reduction in misreporting while with an emission tax, there is no compliance by the firms unless the expected fine, a function of monitoring effort, exceeds the tax rate.
References
Ackermann R, Hanrahan D, Hughes G, Somani A, Aggarwal S, Fitzgerald A (1999) Pollution prevention and abatement handbook 1998—toward cleaner production. The World Bank Group, Washington
Aidt TS (2010) Green taxes: refunding rules and lobbying. J Environ Econ Manag 1:31–43
Aidt TS, Dutta J (2004) Transitional politics. J Environ Econ Manag 3:458–479
Arbatskaya M, Mialon HM (2010) Multi-activity contests. Econ Theory 43:23–43
Australian Government—Department of the Environment (2014) Emission Reduction Fund White Paper, April 2014
Buchanan JM, Tullock G (1975) Polluters’ profits and political response: direct controls versus taxes. Am Econ Rev 65(1):139–147
Chung T-Y (1996) Rent-seeking contest when the prize increases with aggregate efforts. Pub Choice 87(1–2):55–66
Ciocirlan C, Yandle B (2003) The political economy of green taxation in OECD countries. Eur J Law Econ 15(3):203–218
Coase R (1960) The problem of social cost. J Law Econ 3:1–44
D’Amato A, Franckx L (2010) Nonpoint pollution regulation targeted on emission proxies: the role of yardstick schemes. Environ Econ Policy Stud 12(4):201–218
Dijkstra BR (1998) A two-stage rent-seeking contest for instrument choice and revenue division, applied to environmental policy. Eur J Polit Econ 14(2):281–301
Dixit A (1987) Strategic behavior in contests. Am Econ Rev 77(5):891–898
European Commission (2011) Commission Decision of 27 April 2011 determining transitional Union-wide rules for harmonised free allocation of emission allowances pursuant to Article 10a of Directive 2003/87/EC of the European Parliament and of the Council. European Union, 27 April 2011
Fu Q, Lu J (2009) Contest with pre-contest investment. Econ Lett 103(3):142–145
Gerigk J, MacKenzie IA, Ohndorf M (2013) Environmental standards revisited: benchmarking as a means to more efficient regulation. IED working paper series, vol 20, pp 1–32
Govindasamy R, Herriges J, Shogren J (1994) Nonpoint tournaments. In: Tomasi T, Dosi C (eds) Nonpoint-source pollution regulation: issues and analysis. Kluwer, Dordrecht, pp 87–105
Gray WB, Shimshack JP (2011) The effectiveness of environmental monitoring and enforcement: a review of the empirical evidence. Rev Environ Econ Policy 5(1):1–23
Harford JD (1978) Firm behavior under imperfectly enforceable pollution standards and taxes. J Environ Econ Manag 5(1):26–43
Heyes A (2000) Implementing environmental regulation: enforcement and compliance. J Regul Econ 17(2):107–129
Heyes AG (1997) Environmental regulation by private contest. J Pub Econ 3:407–428
Jaffe AB, Peterson SR, Portney PR, Stavins RN (1995) Environmental regulation and the competitiveness of U.S. manufacturing: what does the evidence tell us? J Econ Lit 33(1):132–163
Konrad KA (2009) Strategy and dynamics in contests. Oxford University Press, Oxford
Macho-Stadler I, Perez-Castrillo D (2006) Optimal enforcement policy and firms emissions and compliance with environmental taxes. J Environ Econ Manag 51(1):110–131
MacKenzie I, Hanley N, Kornienko T (2008) The optimal initial allocation of pollution permits: a relative performance approach. Environ Resour Econ 39(3):265–282
MacKenzie IA, Ohndorf M (2012a) Cap-and-trade, taxes, and distributional conflict. J Environ Econ Manag 1:51–65
MacKenzie IA, Ohndorf M (2012b) Optimal monitoring of credit-based emissions trading under asymmetric information. J Regul Econ 2:180–203
Malik AS (1992) Enforcement costs and the choice of policy instruments for controlling pollution. Econ Inq 30(4):714–721
Malueg DA, Yates AJ (2006) Citizen participation in pollution permit markets. J Environ Econ Manag 51(2):205–217
Mitchell C (2000) The England and Wales non-fossil fuel obligation: history and lessons. Ann Rev Energy Environ 25(1):285–312
Montero J-P (2002) Permits, standards, and technology innovation. J Environ Econ Manag 44(1):23–44
Nordic Environment Finance Corporation (NEFCO) (2013) NEFCO Norwegian Carbon Procurement Facility (NorCaP)—Letter of Invitation, November 2013
Oates WE, Portney PR, McGartland AM (1989) The net benefits of incentive-based regulation: a case study of environmental standard setting. Am Econ Rev 79(5):1233–1242
Pigou AC (1920) The economics of welfare. Macmillan and Co, London
Requate T (2005) Dynamic incentives by environmental policy instruments. Ecol Econ 2(3):175–195
Requate T, Unold W (2003) Environmental policy incentives to adopt advanced abatement technology. Eur Econ Rev 1:125–146
Shleifer A (1985) A theory of yardstick competition. RAND J Econ 16(3):319–327
Sterner T, Isaksson LH (2006) Refunded emission payments theory, distribution of costs, and swedish experience of NO\(_x\) abatement. Ecol Econ 1:93–106
Stranlund JK, Chvez CA, Villena MG (2009) The optimal pricing of pollution when enforcement is costly. J Environ Econ Manag 58(2):183–191
Telle K (2013) Monitoring and enforcement of environmental regulations: lessons from a natural field experiment in Norway. J Pub Econ 99:24–34
Tullock G (1980) Efficient rent seeking. In: Buchanan JM, Tollison RD, Tullock G (eds) Toward a theory of the rent-seeking society. Texas A&M University Press, College Station
Acknowledgments
The authors are grateful to two anonymous reviewers and the Editor Anthony Heyes for helpful comments and suggestions that significantly improved this paper. Furthermore, we would like to thank Alessio D’Amato, Johannes Manser, and Renate Schubert as well as seminar participants in Zürich (ETH), Paris (26th International Climate Policy Workshop), Toulouse (EAERE 2013), and Ascona (SURED 2014) for their valuable comments and suggestions. Financial support by the Swiss Academy of Humanities and Social Sciences (SAGW) is gratefully acknowledged. All errors and shortcomings are our own.
Author information
Authors and Affiliations
Corresponding author
Appendices
Mathematical Appendix
1.1 Proof of Proposition 1
Proof
To solve (13) we derive the following set of first-order conditions:
Substitution of the first FOC into the second yields after some simplification
As \(k_i = \frac{1}{\gamma _i + \mu I_i}\), it follows
Substituting (35) into (34) yields the optimal level of investment:
As \(\frac{\partial ^2 \pi _i}{\partial I_i^2}<0\), (36) denotes indeed a maximum.
With \(k_i = \frac{1}{\gamma _i + \mu I_i}\), (36) ultimately defines the cost parameter \(k_i^* = \frac{8}{\mu P}\). Finally, substituting (15) into (13) yields the corresponding payoff:
\(\square \)
1.2 Proof of Proposition 2
Proof
The proof requires solving the game represented by Eq. (17) via backward induction. The solution to the second stage is defined by the following first-order condition:
Equating both first-order conditions, we find \(c_i = c_{-i}\). Solving the game is then straightforward and yields:
where \(k_i = k_i(I_i) = \frac{1}{\gamma _i + \mu I_i}\).
With the solution to the second stage defined by (37)–(40), the objective function reduces to (18). Equating the first-order conditions for \(X\) and \(Y\) yields
To see this, note that there exists no \(\delta \ne 1\) with \(\frac{1}{\gamma _X + \mu I_X} = \delta \cdot \frac{1}{\gamma _Y + \mu I_Y}\), for which the first-order condition holds. From (41) it directly follows that \(k_X = k_Y\).
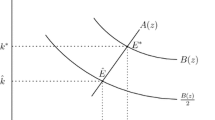
With this finding, the equilibrium level of total abatement reduces to \(\tilde{A}_q = \sqrt{\frac{Pq}{2k_X}}\) and first-best abatement is given by \(A_I^* = \frac{\bar{E}}{b+k_X}\). Equating \(\tilde{A}_q\) and \(A_I^*\), solving for \(q^*\) is straightforward and results in (19).
Note that to ensure consistency of the mechanism’s abatement incentives, \(q\) is constrained such that total abatement under benchmarking regulation, \(\tilde{A}\), increases with higher levels of \(q\); i.e., abatement incentives are consistent iff \(\frac{\partial \tilde{A}_q}{\partial q}>0\):
Hence, for \(k_Y=\sigma k_X, \frac{\partial \tilde{A}_q}{\partial q}{>}0\) iff
A sufficient condition for the mechanism to yield consistent incentives to abate pollution is \(q \cdot \ln (\sigma )-2 <0\) and thus \(q < \frac{2}{\ln (\sigma )}\). \(\square \)
1.3 Proof of Proposition 4
Proof
To derive Proposition 4, we proceed with an unconstrained optimization of (28)—where \(k_Y = \sigma k_X\)—and then derive conditions for potential corner solutions. The unconstrained optimization yields
Hence, for \(\bar{E}>0, \alpha ^* > 0\), thus there is no corner solution at the lower bound of the domain of \(\alpha \). It is also straightforward from (43) that a corner solution \(\alpha ^*=1\) exists iff
where
\(\square \)
1.3.1 Proof of Proposition 5
Proof
To prove Proposition 5, we first show that for an interior solution of \(\alpha ^*, A(\alpha ^*)>A^*\). For \(\alpha ^* \in (0,1), A(\alpha ^*)< A^*\) iff
Condition (46) simplifies to \(1<-\frac{(1+\sigma )^2}{\sqrt{\sigma } (1+\sqrt{\sigma })^2}\), which never holds. Hence, \(\forall \alpha ^* \in (0,1), A(\alpha ^*)>A^*\).
Second, it is straightforward from (44) that \(\alpha ^* = 1\) iff \(\Omega \le \frac{\bar{E}^2}{P}\), where \(\Omega \) is defined in Eq. (32). Finally, from (12) we know that \(A(\alpha ^* \mid \alpha ^*=1)<A^*\) iff \(\Psi < \frac{\bar{E}^2}{P}\), where \(\Psi = \frac{\left( b \sigma + b +2\sigma k_X\right) ^2}{2k_X(1+\sigma )^2 \sqrt{\sigma }}\). This completes the proof. \(\square \)
A Generalized Model with \(n\) Agents
1.1 The Maximization Problem of the Agents
For completeness, we show the results of the model with rent seeking in a generalized framework with \(i = 1, \ldots , n\) firms. For \(i \in \Phi \) and \(-i \in \Phi \backslash \{i\}\), the payoff function of the individual is
First- and second-order conditions allow us to solve for the individual and total equilibrium levels of abatement costs, abatement, and rent seeking.
The first derivative of the payoff function (47) with respect to \(c_i\) is given by
As \(c_1 = c_2 = \cdots = c_i = \cdots = c_n\), we can calculate \(c_i\), which is given by
Total abatement costs \(C\) are simply given by \(\hat{C}_n = n \cdot \hat{c}_{i,n} = \sum _{i=1}^n \hat{a}_{i,n}^2 k_i\).
As we have established that \(a_i = \left( \frac{c_i}{k_i}\right) ^{\frac{1}{2}}\), we can easily compute individual and total abatement levels, i.e., \(\hat{a}_{i,n}\) and \(\hat{A}_n = \sum _{i=1}^{n} \hat{a}_{i,n}\).
The equilibrium level of rent seeking \(\hat{s}_{i,n}\) is derived by using the first-order condition of the payoff function with respect to \(s_i\):
Given that \(s_1 = s_2 = \cdots = s_i = \cdots = s_n\), we have
Aggregate rent seeking is given by the sum of the \(\hat{s}_{i,n}\): \(\hat{S}_n = \sum _{i=1}^n \hat{s}_{i,n} = n \cdot \hat{s}_{i,n}\).
To summarize, if payoffs are defined by (47), the equilibrium is defined by
1.2 Welfare Optimization
We now determine the optimal \(\alpha _n\) by minimizing the costs to society:
where
Rearranging the first-order condition allows one to solve for the interior solution of the optimal \(\alpha \) in the \(n\)-player case:
It is easy to check that this is equivalent to the results of the case with two firms. Therefore, the underlying incentives remain unchanged.
Rights and permissions
About this article
Cite this article
Gerigk, J., MacKenzie, I.A. & Ohndorf, M. A Model of Benchmarking Regulation: Revisiting the Efficiency of Environmental Standards. Environ Resource Econ 62, 59–82 (2015). https://doi.org/10.1007/s10640-014-9815-7
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10640-014-9815-7
Keywords
- Environmental standards
- Command-and-control regulation
- Benchmarking
- Relative performance mechanism
- Contests