Abstract
We provide for the first time an asymptotic comparison of all known algorithms for the search version of the Learning with Errors (LWE) problem. This includes an analysis of several lattice-based approaches as well as the combinatorial BKW algorithm. Our analysis of the lattice-based approaches defines a general framework, in which the algorithms of Babai, Lindner–Peikert and several pruning strategies appear as special cases. We show that within this framework, all lattice algorithms achieve the same asymptotic complexity. For the BKW algorithm, we present a refined analysis for the case of only a polynomial number of samples via amplification, which allows for a fair comparison with lattice-based approaches. Somewhat surprisingly, such a small number of samples does not make the asymptotic complexity significantly inferior, but only affects the constant in the exponent. As the main result we obtain that both, lattice-based techniques and BKW with a polynomial number of samples, achieve running time \(2^{{\mathcal {O}}(n)}\) for n-dimensional LWE, where we make the constant hidden in the big-\({\mathcal {O}}\) notion explicit as a simple and easy to handle function of all LWE-parameters. In the lattice case this function also depends on the time to compute a BKZ lattice basis with block size \(\varTheta (n)\). Thus, from a theoretical perspective our analysis reveals how LWE ’s complexity changes as a function of the LWE-parameters, and from a practical perspective our analysis is a useful tool to choose LWE-parameters resistant to all currently known attacks.


Similar content being viewed by others
Notes
Throughout, we omit the \(o(\cdot )\)-terms: For the \({\texttt {BKZ}} \) running time
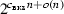 , we use
, we use  .
.For \(s\rightarrow \infty \), the standard deviation is \(s/\sqrt{2\pi }+o(s)\), the \(o(s)\) being due to discretization.
Our runtime analysis is in all cases robust against small deviations from exact equality.
The target and the lattice do not have to agree on dimension in general, but for LWE this is the case (we project \({\mathbf {t}}\) onto \({{\mathrm{Span}}}({\mathcal {L}}({\mathbf {B}}))\) otherwise and work with the projection).
This is equivalent to the problem for target vector \({\mathbf {t}}-{\mathbf {x}}\) and without shift. We use shifts to write the algorithms in a cleaner way via recursion, where shifts will appear in the recursive calls.
On the boundary of \({\mathcal {P}}_{\tiny {1/2}}\widetilde{{\mathbf {B}}}\), it depends on how equally close hyperplanes are handled in line 4 of Algorithm 1; this case will not affect our analysis.
This can be made to hold true even if there are two equally close hyperplanes in the algorithm; these cases do not affect our analysis.
Again, we ignore the case of equally close hyperplanes for NearestPlane(s).
This depends on to what extent we allow reusing the same initial sample in several combinations, as allowed by some variants [34] of BKW at the expense of a heuristic analysis. These modifications have no impact on the asymptotics.
References
Aggarwal D., Dadush D., Regev O., Stephens-Davidowitz N.: Solving the shortest vector problem in \(2^{{\rm n}}\) time via discrete gaussian sampling. In: Proceedings of the Forty-Seventh Annual ACM Symposium on Theory of Computing (STOC ’15), pp. 733–742. ACM, New York (2015).
Ajtai M., Kumar R., Sivakumar D.: A sieve algorithm for the shortest lattice vector problem. In: Proceedings of STOC, pp. 601–610 (2001).
Albrecht M., Faugére J.-C., Fitzpatrick R., Perret L.: Lazy Modulus Switching for the BKW Algorithm on LWE. Lecture Notes in Computer Science, vol. 8383, pp. 429–445. Springer, Berlin (2014).
Albrecht M.R., Player R., Scott S.: On the concrete hardness of learning with errors. Cryptology ePrint Archive, Report 2015/046 (2015).
Albrecht M., Cid C., Faugére J.C., Fitzpatrick R., Perret L.: On the complexity of the bkw algorithm on lwe. Des. Codes Cryptogr. 74(2), 325–354 (2013).
Alkim E., Ducas L., Pöppelmann T., Schwabe P.: Post-quantum key exchange —a new hope. In: Proceedings of the 25th USENIX Security Symposium. USENIX Association (2016).
Aono Y., Boyen X., Phong L., Wang L.: Key-private proxy re-encryption under LWE. In: INDOCRYPT 2013, pp. 1–18 (2013).
Applebaum B., Cash D., Peikert C., Sahai A.: Fast cryptographic primitives and circular-secure encryption based on hard learning problems. In: Advances in Cryptology—CRYPTO 2009. Lecture Notes in Computer Science, vol. 5677, pp. 595–618. Springer, Berlin (2009).
Arora S., Ge R.: New algorithms for learning in presence of errors. In: Proceedings of the 38th International Colloquim Conference on Automata, Languages and Programming (ICALP’11), pp. 403–415 (2011).
Babai L.: On Lovász’ lattice reduction and the nearest lattice point problem (shortened version). In: STACS, pp. 13–20 (1985).
Banaszczyk W.: New bounds in some transference theorems in the geometry of numbers. Math. Ann. 296(1), 625–635 (1993).
Becker A., Ducas L., Gama N., Laarhoven T.: New directions in nearest neighbor searching with applications to lattice sieving. In: SODA (2016).
Blum A., Kalai A.: Noise-tolerant learning, the parity problem, and the statistical query model. J. ACM 50, 506–519 (2003).
Bos J., Costello C., Ducas L., Mironov I., Naehrig M., Nikolaenko V., Raghunathan A., Stebila D.: Frodo: Take off the ring! practical, quantum secure key exchange from LWE. In: Proceedings of the 2016 ACM SIGSAC Conference on Computer and Communications Security, CCS ’16, pp. 1006–1018, (2016).
Brakerski Z., Langlois A., Peikert C., Regev O., Stehlé D.: Classical hardness of learning with errors. In: Proceedings of STOC, pp. 575–584 (2013).
Döttling N.: Low noise LPN: KDM secure public key encryption and sample amplification. In: Public-Key Cryptography—PKC 2015—Proceedings of the 18th IACR International Conference on Practice and Theory in Public-Key Cryptography, Gaithersburg, MD, 30 March–1 April 2015, pp. 604–626 (2015).
Duc A., Tramér F., Vaudenay S.: Better algorithms for LWE and LWR. In: EUROCRYPT (2015).
Fincke U., Pohst M.: A procedure for determining algebraic integers of given norm. In: Proceedings of EUROCAL. Lecture Notes in Computer Science, vol. 162, pp. 194–202 (1983).
Gama N., Nguyen P.Q.: Predicting lattice reduction. In: EUROCRYPT, pp. 31–51 (2008).
Gama N., Nguyen P., Regev O.: Lattice enumeration using extreme pruning. In: EUROCRYPT 2010, LNCS, vol. 6110, pp. 257–278. Springer, Berlin (2010).
Gentry C., Peikert C., Vaikuntanathan V.: Trapdoors for hard lattices and new cryptographic constructions. In: STOC ’08, pp. 197–206 (2008).
Goldreich O., Goldwasser S.: On the limits of nonapproximability of lattice problems. J. Comput. Syst. Sci. 60(3), 540–563 (2000).
Goldreich O., Rubinfeld R., Sudan M.: Learning polynomials with queries: the highly noisy case. In: Proceedings of the 36th Annual Symposium on Foundations of Computer Science, FOCS, pp. 294–303 (1995).
Guo Q., Johansson T., Stankovski P.: Coded-BKW: solving LWE using lattice codes. In: Advances in Cryptology—CRYPTO 2015. Lecture Notes in Computer Science, vol. 9215, pp. 23–42. Springer, Berlin (2015).
Hanrot G., Stehlé D.: Improved analysis of kannans shortest lattice vector algorithm. In: Advances in Cryptology—CRYPTO 2007, LNCS, vol. 4622, pp. 170–186 (2007).
Hanrot G., Pujol X., Stehlé D.: Analyzing Blockwise Lattice Algorithms Using Dynamical Systems, LNCS, vol. 6841, pp. 447–464. Springer, Berlin (2011).
Kannan R.: Improved algorithms for integer programming and related lattice problems. In: Proceedings of STOC, pp. 193–206 (1983).
Kannan R.: Minkowski’s convex body theorem and integer programming. Math. Oper. Res. 12, 415–440 (1987).
Kirchner P., Fouque P.: An improved BKW algorithm for LWE with applications to cryptography and lattices. In: Advances in Cryptology—CRYPTO 2015. Lecture Notes in Computer Science, vol. 9215, pp. 43–62. Springer, Berlin (2015)
Kirshanova E., May A., Wiemer F.: Parallel Implementation of BDD Enumeration for LWE, pp. 580–591. Springer, Cham (2016).
Kleinjung T., Aoki K., Franke J., Lenstra A.K., Thomé E., Bos J.W., Gaudry P., Kruppa A., Montgomery P.L., Osvik D.A., et al. Factorization of a 768-bit rsa modulus. In: Advances in Cryptology—CRYPTO 2010, pp. 333–350. Springer, Berlin (2010).
Laarhoven T.: Sieving for shortest vectors in lattices using angular locality-sensitive hashing. In: CRYPTO (2015).
Lenstra A.K., Verheul E.R.: Selecting cryptographic key sizes. J. Cryptol. 14(4), 255–293 (2001).
Levieil É., Fouque P.-A.: An improved LPN algorithm. In: Security and Cryptography for Networks. Lecture Notes in Computer Science, vol. 4116, pp. 348–359. Springer, Berlin (2006).
Lindner R., Peikert C.: Better key sizes (and attacks) for LWE-based encryption. In: CT-RSA’11, pp. 319–339 (2011).
Liu M., Nguyen P.Q.: Solving BDD by enumeration: an update. In: CT-RSA, pp. 293–309 (2013).
Lyubashevsky V.: The parity problem in the presence of noise, decoding random linear codes, and the subset sum problem. In: RANDOM. Lecture Notes in Computer Science, vol. 3624, pp. 378–389. Springer, Berlin (2005).
Lyubashevsky V., Micciancio D.: On bounded distance decoding, unique shortest vectors, and the minimum distance problem. In: Advances in Cryptology—CRYPTO 2009. Lecture Notes in Computer Science, vol. 5677, pp. 577–594. Springer, Berlin (2009).
Micciancio D., Goldwasser S.: Complexity of Lattice Problems: A Cryptographic Perspective. The Kluwer International Series in Engineering and Computer Science. Kluwer Academic, Boston (2002).
Micciancio D., Regev O.: Worst-case to average-case reductions based on Gaussian measures. SIAM J. Comput. 372–381 (2004).
Micciancio D., Regev O.: Lattice-Based Cryptography. Springer, Berlin (2009).
Micciancio D., Voulgaris P.: A deterministic single exponential time algorithm for most lattice problems based on voronoi cell computations. In: Proceedings of STOC ’10, pp. 351–358 (2010).
Peikert C.: Public-key cryptosystems from the worst-case shortest vector problem: extended abstract. In: Proceedings of STOC, pp. 333–342 (2009).
Peikert C., Micciancio D.: Trapdoors for lattices: simpler, tighter, faster, smaller. In: EUROCRYPT, pp. 700–718 (2012).
Rado R.: A theorem on the geometry of numbers. J. Lond. Math. Soc. s1–21(1), 34–47 (1946).
Regev O.: On lattices, learning with errors, random linear codes, and cryptography. In: STOC, pp. 84–93. ACM Press, New York (2005).
Schnorr C.-P.: Lattice reduction by random sampling and birthday methods. In: STACS, pp. 145–156 (2003).
Schnorr C.-P., Euchner M.: Lattice basis reduction: improved practical algorithms and solving subset sum problems. Math. Program. 66, 181–191 (1993).
Yearly report on algorithms and keysizes. D.SPA.20 Rev. 1.0, ICT-2007-216676 ECRYPT II (2012).
Acknowledgements
Funding was provided by Deutschen Forschungsgemeinschaft (DFG) (Grant Nos. GRK 817 Ubicrypt, UbiCrypt (GRK 1817/1)) and FSC: Fast and Sound Cryptography (Grant No. ERC Starting Grant 307952).
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by L. Perret.
Rights and permissions
About this article
Cite this article
Herold, G., Kirshanova, E. & May, A. On the asymptotic complexity of solving LWE. Des. Codes Cryptogr. 86, 55–83 (2018). https://doi.org/10.1007/s10623-016-0326-0
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10623-016-0326-0





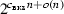 , we use
, we use  .
.