Skip to main content

Advertisement

SpringerLink
Log in

Interpretable time series classification using linear models and multi-resolution multi-domain symbolic representations

  • Published:
Data Mining and Knowledge Discovery Aims and scope Submit manuscript

Abstract

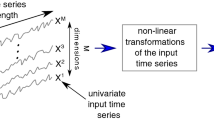
The time series classification literature has expanded rapidly over the last decade, with many new classification approaches published each year. Prior research has mostly focused on improving the accuracy and efficiency of classifiers, with interpretability being somewhat neglected. This aspect of classifiers has become critical for many application domains and the introduction of the EU GDPR legislation in 2018 is likely to further emphasize the importance of interpretable learning algorithms. Currently, state-of-the-art classification accuracy is achieved with very complex models based on large ensembles (COTE) or deep neural networks (FCN). These approaches are not efficient with regard to either time or space, are difficult to interpret and cannot be applied to variable-length time series, requiring pre-processing of the original series to a set fixed-length. In this paper we propose new time series classification algorithms to address these gaps. Our approach is based on symbolic representations of time series, efficient sequence mining algorithms and linear classification models. Our linear models are as accurate as deep learning models but are more efficient regarding running time and memory, can work with variable-length time series and can be interpreted by highlighting the discriminative symbolic features on the original time series. We advance the state-of-the-art in time series classification by proposing new algorithms built using the following three key ideas: (1) Multiple resolutions of symbolic representations: we combine symbolic representations obtained using different parameters, rather than one fixed representation (e.g., multiple SAX representations); (2) Multiple domain representations: we combine symbolic representations in time (e.g., SAX) and frequency (e.g., SFA) domains, to be more robust across problem types; (3) Efficient navigation in a huge symbolic-words space: we extend a symbolic sequence classifier (SEQL) to work with multiple symbolic representations and use its greedy feature selection strategy to effectively filter the best features for each representation. We show that our multi-resolution multi-domain linear classifier (mtSS-SEQL+LR) achieves a similar accuracy to the state-of-the-art COTE ensemble, and to recent deep learning methods (FCN, ResNet), but uses a fraction of the time and memory required by either COTE or deep models. To further analyse the interpretability of our classifier, we present a case study on a human motion dataset collected by the authors. We discuss the accuracy, efficiency and interpretability of our proposed algorithms and release all the results, source code and data to encourage reproducibility.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16

Similar content being viewed by others

Notes

  1. According to our experiments comparing single SAX vs single SFA classifiers, shown in Sect. 4.

  2. Experiments and discussion backing these statements are available in Sects. 5 and  7.

  3. http://www.timeseriesclassification.com/results.php.

  4. https://www2.informatik.hu-berlin.de/~schaefpa/weasel/.

  5. https://github.com/hfawaz/dl-4-tsc.

  6. https://github.com/astrofrog/psrecord.

  7. The error rates of mtSAX-SEQL+LR, mtSFA-SEQL+LR and mtSS-SEQL+LR were comparable, but we only discuss mtSAX-SEQL+LR here since it is also interpretable. Note that we used a default number of symbolic representations/resolutions for mtSAX-SEQL+LR (increasing the window length with a step \(\sqrt{L}\)). By increasing the number of SAX representations, we can further improve the accuracy of mtSAX-SEQL+LR, as also discussed in Sect. 5.3.

References

  • Bagnall A, Lines J, Hills J, Bostrom A (2015) Time-series classification with cote: the collective of transformation-based ensembles. IEEE Trans Knowl Data Eng 27(9):2522–2535

    Article  Google Scholar 

  • Bagnall A, Lines J, Bostrom A, Large J, Keogh E (2017) The great time series classification bake off: a review and experimental evaluation of recent algorithmic advances. Data Min Knowl Discov 31(3):606–660. https://doi.org/10.1007/s10618-016-0483-9

    Article  MathSciNet  Google Scholar 

  • Baydogan MG, Runger G, Tuv E (2013) A bag-of-features framework to classify time series. IEEE Trans Pattern Anal Mach Intell 35(11):2796–2802. https://doi.org/10.1109/TPAMI.2013.72

    Article  Google Scholar 

  • Benavoli A, Corani G, Mangili F (2016) Should we really use post-hoc tests based on mean-ranks? J Mach Learn Res 17(5):1–10

    MathSciNet  MATH  Google Scholar 

  • Bostrom A, Bagnall A (2015) Binary shapelet transform for multiclass time series classification. In: Madria S, Hara T (eds) Big data analytics and knowledge discovery. Springer International Publishing, Cham, pp 257–269

    Chapter  Google Scholar 

  • Briandet R, Kemsley EK, Wilson RH (1996) Discrimination of arabica and robusta in instant coffee by fourier transform infrared spectroscopy and chemometrics. J Agric Food Chem 44(1):170–174. https://doi.org/10.1021/jf950305a

    Article  Google Scholar 

  • Calvo B, Santaf G (2016) scmamp: statistical comparison of multiple algorithms in multiple problems. R J 8(1):248–256. https://doi.org/10.32614/RJ-2016-017

    Article  Google Scholar 

  • Castro N, Azevedo P (2010) Multiresolution Motif Discovery in Time Series, pp 665–676. https://doi.org/10.1137/1.9781611972801.73

  • Chen JS, Moon YS, Yeung HW (2005) Palmprint authentication using time series. In: Kanade T, Jain A, Ratha NK (eds) Audio- and video-based biometric person authentication. Springer, Berlin, pp 376–385

    Chapter  Google Scholar 

  • Chen Y, Keogh E, Hu B, Begum N, Bagnall A, Mueen A, Batista G (2015) The ucr time series classification archive. www.cs.ucr.edu/~eamonn/time_series_data/

  • Costa da Silva J, Klusch M (2007) Privacy-preserving discovery of frequent patterns in time series. In: Perner P (ed) Advances in data mining. Theoretical aspects and applications. Springer, Berlin, pp 318–328

    Chapter  Google Scholar 

  • Demšar J (2006) Statistical comparisons of classifiers over multiple data sets. J Mach Learn Res 7:1–30

    MathSciNet  MATH  Google Scholar 

  • Garcia S, Herrera F (2008) An extension on ”statistical comparisons of classifiers over multiple data sets” for all pairwise comparisons. J Mach Learn Res 9:2677–2694

    MATH  Google Scholar 

  • Glatthorn JF, Gouge S, Nussbaumer S, Stauffacher S, Impellizzeri FM, Maffiuletti NA (2011) Validity and reliability of optojump photoelectric cells for estimating vertical jump height. J Strength Cond Res 25(2):556–560

    Article  Google Scholar 

  • Gordon D, Hendler D, Rokach L (2012) Fast randomized model generation for shapelet-based time series classification. CoRR arXiv:abs/1209.5038

  • Grabocka J, Schilling N, Wistuba M, Schmidt-Thieme L (2014) Learning time-series shapelets. In: Proceedings of the 20th ACM SIGKDD international conference on knowledge discovery and data mining, ACM, New York, NY, USA, KDD ’14, pp 392–401, https://doi.org/10.1145/2623330.2623613

  • Ifrim G, Wiuf C (2011) Bounded coordinate-descent for biological sequence classification in high dimensional predictor space. In: Proceedings of the 17th ACM SIGKDD international conference on knowledge discovery and data mining, ACM, New York, NY, USA, KDD ’11, pp 708–716, https://doi.org/10.1145/2020408.2020519

  • Ismail Fawaz H, Forestier G, Weber J, Idoumghar L, Muller PA (2019) Deep learning for time series classification: a review. Data Mining Knowl Discov. https://doi.org/10.1007/s10618-019-00619-1

    Article  MathSciNet  Google Scholar 

  • Kasten EP, McKinley PK, Gage SH (2007) Automated ensemble extraction and analysis of acoustic data streams. In: 27th International conference on distributed computing systems workshops (ICDCSW’07), pp 66–66, https://doi.org/10.1109/ICDCSW.2007.25

  • Kate RJ (2016) Using dynamic time warping distances as features for improved time series classification. Data Mining Knowl Discov 30(2):283–312. https://doi.org/10.1007/s10618-015-0418-x

    Article  MathSciNet  MATH  Google Scholar 

  • Keogh E, Chakrabarti K, Pazzani M, Mehrotra S (2001) Dimensionality reduction for fast similarity search in large time series databases. Knowl Inf Syst 3(3):263–286. https://doi.org/10.1007/PL00011669

    Article  MATH  Google Scholar 

  • Lin J, Keogh E, Lonardi S, Chiu B (2003) A symbolic representation of time series, with implications for streaming algorithms. In: Proceedings of the 8th ACM SIGMOD workshop on research issues in data mining and knowledge discovery, ACM, New York, NY, USA, DMKD ’03, pp 2–11, https://doi.org/10.1145/882082.882086

  • Lin J, Keogh E, Wei L, Lonardi S (2007) Experiencing sax: a novel symbolic representation of time series. Data Mining Knowl Discov 15(2):107–144. https://doi.org/10.1007/s10618-007-0064-z

    Article  MathSciNet  Google Scholar 

  • Lin J, Khade R, Li Y (2012) Rotation-invariant similarity in time series using bag-of-patterns representation. J Intell Inf Syst 39(2):287–315. https://doi.org/10.1007/s10844-012-0196-5

    Article  Google Scholar 

  • Lines J, Bagnall A (2015) Time series classification with ensembles of elastic distance measures. Data Min Knowl Discov 29(3):565–592. https://doi.org/10.1007/s10618-014-0361-2

    Article  MathSciNet  MATH  Google Scholar 

  • Lines J, Davis LM, Hills J, Bagnall A (2012) A shapelet transform for time series classification. In: Proceedings of the 18th ACM SIGKDD international conference on knowledge discovery and data mining, ACM, New York, NY, USA, KDD ’12, pp 289–297, https://doi.org/10.1145/2339530.2339579

  • Lines J, Taylor S, Bagnall A (2016) Hive-cote: The hierarchical vote collective of transformation-based ensembles for time series classification. In: 2016 IEEE 16th international conference on data mining (ICDM), pp 1041–1046, https://doi.org/10.1109/ICDM.2016.0133

  • Markovic G, Dizdar D, Jukic I, Cardinale M (2004) Reliability and factorial validity of squat and countermovement jump tests. J Strength Cond Res 18(3):551–555

    Google Scholar 

  • Nguyen TL, Gsponer S, Ifrim G (2017) Time series classification by sequence learning in all-subsequence space. In: 2017 IEEE 33rd international conference on data engineering (ICDE), pp 947–958, https://doi.org/10.1109/ICDE.2017.142

  • Nuzzo JL, McBride JM, Cormie P, McCaulley GO (2008) Relationship between countermovement jump performance and multijoint isometric and dynamic tests of strength. J Strength Cond Res 22(3):699–707. https://doi.org/10.1519/jsc.0b013e31816d5eda

    Article  Google Scholar 

  • O’Reilly M, Caulfield B, Ward T, Johnston W, Doherty C (2018) Wearable inertial sensor systems for lower limb exercise detection and evaluation: a systematic review. Sports Medicine pp 1–26

  • O’Reilly MA, Whelan DF, Ward TE, Delahunt E, Caulfield BM (2017) Classification of deadlift biomechanics with wearable inertial measurement units. J Biomech 58:155–161. https://doi.org/10.1016/j.jbiomech.2017.04.028

    Article  Google Scholar 

  • Picerno P, Camomilla V, Capranica L (2011) Countermovement jump performance assessment using a wearable 3d inertial measurement unit. J Sports Sci 29(2):139–146, https://doi.org/10.1080/02640414.2010.523089, pMID: 21120742

  • Rakthanmanon T, Keogh E (2013) Fast shapelets: A scalable algorithm for discovering time series shapelets. In: Proceedings of the thirteenth SIAM conference on data mining (SDM), SIAM, pp 668–676

  • Schäfer P (2015) The boss is concerned with time series classification in the presence of noise. Data Min Knowl Discov 29(6):1505–1530

    Article  MathSciNet  MATH  Google Scholar 

  • Schäfer P (2016) Scalable time series classification. Data Min Knowl Discov 30(5):1273–1298. https://doi.org/10.1007/s10618-015-0441-y

    Article  MathSciNet  MATH  Google Scholar 

  • Schäfer P, Högqvist M (2012) Sfa: A symbolic fourier approximation and index for similarity search in high dimensional datasets. In: Proceedings of the 15th international conference on extending database technology, ACM, New York, NY, USA, EDBT ’12, pp 516–527, https://doi.org/10.1145/2247596.2247656

  • Schäfer P, Leser U (2017) Fast and accurate time series classification with weasel. In: Proceedings of the 2017 ACM on conference on information and knowledge management, ACM, New York, NY, USA, CIKM ’17, pp 637–646, https://doi.org/10.1145/3132847.3132980

  • Schäfer P, Leser U (2017) Multivariate time series classification with WEASEL+MUSE. CoRR arXiv:abs/1711.11343

  • Senin P, Malinchik S (2013) Sax-vsm: Interpretable time series classification using sax and vector space model. In: 2013 IEEE 13th international conference on data mining (ICDM), pp 1175–1180, https://doi.org/10.1109/ICDM.2013.52

  • Wang X, Mueen A, Ding H, Trajcevski G, Scheuermann P, Keogh E (2013) Experimental comparison of representation methods and distance measures for time series data. Data Min Knowl Discov 26(2):275–309

    Article  MathSciNet  Google Scholar 

  • Wang Z, Yan W, Oates T (2017) Time series classification from scratch with deep neural networks: a strong baseline. In: 2017 international joint conference on neural networks (IJCNN), pp 1578–1585, https://doi.org/10.1109/IJCNN.2017.7966039

  • Ye L, Keogh E (2009) Time series shapelets: a new primitive for data mining. In: Proceedings of the 15th ACM SIGKDD international conference on knowledge discovery and data mining, ACM, pp 947–956

  • Ye L, Keogh E (2011) Time series shapelets: a novel technique that allows accurate, interpretable and fast classification. Data Min Knowl Discov 22(1):149–182. https://doi.org/10.1007/s10618-010-0179-5

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

We would like to thank the anonymous reviewers for their detailed and constructive feedback. We would also like to gratefully acknowledge the work by researchers at University of California Riverside, USA (especially Eamonn Keogh and his team) and researchers at University of East Anglia, UK (especially Tony Bagnall and his team) and their effort in collecting, updating and making available the UCR and UEA time series classification benchmarks. We want to thank all researchers in time series classification who have made their data, code and results open source and have helped the reproducibility of research methods in this area. We acknowledge financial support for this work by Science Foundation Ireland (SFI) under grant number 12/RC/2289 (Insight Centre for Data Analytics).

Author information

Authors and Affiliations

  1. Insight Centre for Data Analytics, University College Dublin, Dublin, Ireland

    Thach Le Nguyen, Severin Gsponer, Iulia Ilie, Martin O’Reilly & Georgiana Ifrim

Authors
  1. Thach Le Nguyen
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Severin Gsponer
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Iulia Ilie
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Martin O’Reilly
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Georgiana Ifrim
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding authors

Correspondence to Thach Le Nguyen or Georgiana Ifrim.

Additional information

Responsible editor: Dr. Panagiotis Papapetrou.

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Electronic supplementary material

Below is the link to the electronic supplementary material.

Supplementary material 1 (pdf 457 KB)

Supplementary material 2 (csv 15 KB)

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Le Nguyen, T., Gsponer, S., Ilie, I. et al. Interpretable time series classification using linear models and multi-resolution multi-domain symbolic representations. Data Min Knowl Disc 33, 1183–1222 (2019). https://doi.org/10.1007/s10618-019-00633-3

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10618-019-00633-3

Keywords

Search

Navigation