Classification-driven temporal discretization of multivariate time series

Abstract

Biomedical data, in particular electronic medical records data, include a large number of variables sampled in irregular fashion, often including both time point and time intervals, thus providing several challenges for analysis and data mining. Classification of multivariate time series data is a challenging task, but is often necessary for medical care or research. Increasingly, temporal abstraction, in which a series of raw-data time points is abstracted into a set of symbolic time intervals, is being used for classification of multivariate time series. In this paper, we introduce a novel supervised discretization method, geared towards enhancement of classification accuracy, which determines the cutoffs that will best discriminate among classes through the distribution of their states. We present a framework for classification of multivariate time series analysis, which implements three phases: (1) application of a temporal-abstraction process that transforms a series of raw time-stamped data points into a series of symbolic time intervals (based on either unsupervised or supervised temporal abstraction); (2) mining these time intervals to discover frequent temporal-interval relation patterns (TIRPs), using versions of Allen’s 13 temporal relations; (3) using the patterns as features to induce a classifier. We evaluated the framework, focusing on the comparison of three versions of the new, supervised, temporal discretization for classification (TD4C) method, each relying on a different symbolic-state distribution-distance measure among outcome classes, to several commonly used unsupervised methods, on real datasets in the domains of diabetes, intensive care, and infectious hepatitis. Using only three abstract temporal relations resulted in a better classification performance than using Allen’s seven relations, especially when using three symbolic states per variable. Similarly when using the horizontal support and mean duration as the TIRPs feature representation, rather than a binary (existence) representation. The classification performance when using the three versions of TD4C was superior to the performance when using the unsupervised (EWD, SAX, and KB) discretization methods.

1 Introduction

The increasing use and availability of longitudinal electronic data in biomedical domains presents a significant opportunity to discover new medical knowledge from multivariate, time-oriented clinical data, and to perform various classification tasks based on the temporal data, such as for purposes of diagnosis (e.g., a correct interpretation of a series of clinical data), plan recognition (e.g., recognizing and understanding a care provider’s plan), quality assessment (e.g., comparing the course of therapy to a gold standard pattern emerging from the records of multiple other patients), and prediction of meaningful clinical outcomes.

However, temporal data in general, and in biomedical domains in particular, include not only time-stamped raw data, or time points (e.g., a temperature of $39.7\,^{\circ }\mathrm{C}$, at 18:50 p.m., on April 11th, 2010), but also temporal intervals, possibly at a higher level of abstraction, which are either a part of the original raw input data (e.g., administration of the Amoxicillin antibiotic medication, 875 mg twice a day, for 14 days), or are abstractions, or interpretations, derived from them (e.g., three days of high fever, or two weeks of high-dose antibiotics). Thus, special care must be taken when processing time-oriented clinical data, in particular for the purpose of discovering new and meaningful knowledge from these data.

Classification of temporal data, especially of both uni-variate and multivariate time series, is a highly challenging as well as an important task in many domains, such as information security, in which classification can be used for malware detection (Moskovitch et al. 2008), financial domains, in which behavioral classification can detect patterns of potential fraud, and many other time-oriented domains. However, it is especially essential in a multitude of different medical domains, in which correct classification of time-series data has immediate implications for diagnosis, for quality assessment, and for prediction of meaningful outcomes (Sacchi et al. 2007; Moskovitch et al. 2009; Batal et al. 2012, 2013; Hauskrecht et al. 2013). In the information security domain, it might enable classification of hardware devices into infected and non-infected, by their temporal behavior (Stopel et al. 2006a, b; Moskovitch et al. 2007a). Longitudinal data, especially multivariate data, are often complex, are typically heterogeneous in type and in format, and are usually measured in irregular time periods. Thus, a framework that unifies the representation and analysis of the multiple time-oriented variables and formats is essential. Recent studies (Sacchi et al. 2007; Patel et al. 2008; Moskovitch et al. 2009; Batal et al. 2012, 2013), particularly in the biomedical domain, increasingly propose the use of temporal abstraction as a preprocessing stage and the use of time-intervals mining for feature extraction. Abstraction might lose some information, but might often greatly enhance generalization, and thus accelerate learning. Thus, this study proposes for those who choose to use this approach a novel supervised method for determining the cutoff values for generating the states from the continuous variables’ data, driven by the temporal distribution of the values.

Until now, almost of the studies that applied state-based temporal abstraction used unsupervised methods, such as EWD or SAX, in addition to knowledge-based, domain-specific, range-discretization definitions. In this paper, however, we first present a method that learns in a supervised manner how to optimally discretize each temporal variable, in order to transform the time-point series into a time-interval series, mine these time-interval series, and perform classification. We then proceed to evaluate the method within several different clinical domains.

Figure 1 illustrates the problem of classifying both various time-point series data and time-interval series data, representing various temporal variables within the same input dataset. Not only are the time points and intervals intermixed, but the time point series might be sampled or recorded at different frequencies: Sampling might occur at a fixed frequency, which may further vary for each type of variable, as shown in Fig. 1 for time series (a) and (b), which is often the case for automated sampling; or at random periods, as often occurs in manual measurements, as illustrated by time series (c).

Fig. 1

The multiple formats of input data for time series analysis include time-points (a, b, c) as well as time-intervals (d, e). Both time-stamped and interval-based data might be sampled at varying frequencies, or, in the case of intervals, include varying durations

Often, certain time-stamped data points might be missing, or their measurements might include an error. Raw data (and certainly abstractions derived from the data) might also be represented by time intervals, such as medication-administration periods, as shown in series (d), in which the duration of the events is constant, and in series (e), in which the temporal duration is varying.

Designing algorithms capable of learning from such data, characterized in various forms, is a challenging topic in temporal data mining research, especially for the purpose of classification. Common classification of multivariate time series methods such as Hidden Markov Model (Rabiner 1989) or recurrent neural network, time series similarity measures (e.g., Euclidean distance or Dynamic Time Warping (Ratanamahatana and Keogh 2005) and time series feature extraction methods (e.g., discrete Fourier transform, discrete wavelet transform or singular value decomposition) cannot be directly applied to such temporal data.

Hu et al. (2013) pointed out that most of the studies in time series classification had unrealistic underlying assumptions, referring specifically to two relevant assumptions: (1) that perfectly aligned atomic patterns can be obtained, and (2) that the patterns are of equal lengths. Although Hu et al. are referring in their examples to uni-variate time series, the critique is at least as relevant to multivariate time series classification. Unlike the approaches that Hu et al. have considered, the approach we will present here doesn’t make any of these assumptions, and mines the data as they are, without any alignment pre-processing.

Moreover, as we describe later, the temporal patterns that we discover have varying temporal durations within each pattern. Finally, the duration of the pattern (or of its components) is not part of a pattern’s explicit or implicit definition; the pattern’s supporting instances can vary in their overall duration, but they are similar with respect to the temporal relations among their symbolic interval-based components.

Thus, in order to classify multivariate time series datasets having various forms of time stamped data, we propose to transform the time point series into a symbolic time interval series representation. Such a representation provides a uniform format of the various temporal variables, which enables us to analyze the relations among the symbolic time intervals derived from the variables’ raw time-stamped data, such as through the discovery of frequent temporal patterns. As we explain in Sect. 2, there are several approaches to the performance of the task of converting the raw time-stamped data into a series of symbolic time intervals, typically at a higher level of conceptual abstraction, a task that we refer to as temporal abstraction; some of these approaches exploit context-sensitive knowledge acquired from human experts (Shahar et al. 1999), while others are purely automatic (Azulay et al. 2007; Höppner 2002; Mörchen and Ultsch 2005). Conceptual representation is common in the medical domain, and was found effective in medical information retrieval too (Moskovitch et al. 2004).

The use of TIRPs as features for the classification of multivariate time series was proposed first in (Patel et al. 2008). The approach was inspired by the Bag-Of-Words in text categorization (Salton et al. 1975), in which words are used as features for the classification of a given document. In our case, the discovered TIRPs from a given period of multivariate time series are used as features, which we call a Bag-Of-TIRPs, and is the focus of this paper. Since these early studies, several additional studies were published exploring the use of frequent TIRPs as classification features for multivariate time series classification (Sacchi et al. 2007; Patel et al. 2008; Batal et al. 2012, 2013). However, all of the previous studies used unsupervised methods for the abstraction of the time-stamped variables into discrete states, such as Equal Width Discretization, Gaussian based methods such as SAX (Lin et al. 2003), and knowledge based methods (Shahar 1997).

In this paper, we introduce the Temporal Discretization for Classification (TD4C) method, a novel supervised temporal discretization method that increases the eventual classification accuracy, after frequent interval-based temporal patterns are discovered and are used as features within the classification process.

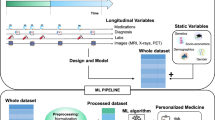
The KarmaLegoSification (KarmaLegoS) framework that embodies the overall temporal classification process is presented in the general block diagram shown in Fig. 2. The input data include multiple instances of entities (e.g., patients, or hardware devices) whose multiple variables (e.g., Hemoglobin value or Number of processes) are described by multivariate time-point series. The time-point series are abstracted, based on domain knowledge (a knowledge-based [KB] method), or on other computational means, and are transformed into symbolic-value time intervals (e.g., Moderate-Anemia from $t_{1}$ to $t_{2}$). The first phase in the process, in which the time point series are abstracted into symbolic time intervals, includes the main contribution of the current paper, i.e., the TD4C method.

Fig. 2

The KarmaLegoSification process, which uses frequent temporal patterns as features for classification of time series. The raw-data time-point and time-interval series are abstracted into a uniform format of symbolic time intervals, using domain-specific knowledge or general computational means. The TD4C method is one option for the abstraction of raw data values into symbolic values, which are then converted into symbolic intervals. The symbolic time intervals are then mined using the KarmaLego algorithm, and a tree of enumerated frequent time interval relation patterns (TIRPs) is generated. The frequent TIRPs are used as features by one or more classification algorithms to produce (induce) a classifier

Temporal abstraction enables us to overcome much of the problems of varying-frequency measurements and recordings, and of minor measurement errors and deviations in the raw data, through the creation of concepts that are no longer time-stamped, raw data, but rather interval-based abstractions, or interpretations, of these data, and through the smoothing effect of these abstractions. In many instances, the temporal-abstraction process also alleviates the problem of missing values, through a process of interpolation across temporal gaps that is inherent in several of the temporal-abstraction methods (see Sect. 2). Note that raw-data interval-based concepts such as “10 Days of Penicillin administration” might simply remain at the same level of abstraction. Whatever the temporal abstraction approach used, having the dataset represented by time intervals series, enables us to discover frequent Time Intervals Related Patterns (TIRPs) (Kam and Fu 2000; Höppner 2001; Mörchen 2006; Sacchi et al. 2007; Patel et al. 2008; Papapetrou et al. 2009; Moskovitch and Shahar 2013; Winarko and Roddick 2007).

Following the abstraction of the time-stamped raw data, the resultant symbolic time intervals are mined using the KarmaLego algorithm, which we introduce in Sect. 3 in detail, to discover frequently repeating temporal patterns. The discovered TIRPs are used as features for the induction of the classifier.

After a TIRP tree is discovered using KarmaLego, several major application categories exist. These potential applications include: Further temporal knowledge discovery, in which a domain expert manually reviews the discovered TIRPs using a tool that we refer to as KarmaLegoVisualization (KLV) (Moskovitch and Shahar 2009); Temporal clustering, in which each temporal pattern is considered as a cluster of entities (e.g., patients, mobile devices) who have similar temporal behavior; extraction of Prediction rules, based on the discovered TIRPs and the transition probabilities between the components of the patterns; and Classification, in which the discovered TIRPs are used as features for a classification task, on which we shall focus in the current paper.

The main contributions of the current paper can be summed up as follows:

• 1. Introducing a novel methodology for discretization of time series, which is driven by the objective of classification of the multivariate time series using a finite number of classes;

• 2. Rigorously evaluating the temporal discretization process and its implications for the discovery of frequent temporal patterns, and for the eventual accuracy of the classification that uses the new discretization method, within an overall framework for temporal data mining and classification, by applying it to several different real-life datasets.

The rest of this paper is organized as follows: We start by introducing briefly, in the Background (Sect. 2), the concepts of temporal data mining, temporal abstraction, temporal discretization, time-interval pattern mining, and classification based on patterns—specifically, based on time-interval patterns. We then introduce in the Methods (Sect. 3) TD4C, a temporal discretization method developed specifically for the classification of multivariate time series, and briefly present a fast time-intervals mining method that we had developed, called KarmaLego, and show how it can be used to discover frequent TIRPs. We also explain exactly how TIRPs are used as features in our temporal data mining framework. In Sect. 4, we describe our detailed evaluation of the efficacy of three versions of the TD4C method, comparing them to the knowledge-based, equal-width, and SAX discretization methods, with respect to the accuracy of an eventual TIRP-based classification, using the discretized values of the same time-stamped input data. We summarize our main contributions and discuss their implications in Sect. 5.

2 Background

2.1 Temporal data mining

Temporal data mining is a sub-field of data mining, in which various techniques are applied to time-oriented data to discover temporal knowledge, i.e. knowledge about relationships amongst different raw-data and abstract concepts, in which the temporal dimension is treated explicitly. Unlike common data mining methods, which are static, often ignoring the temporal dimension, or using only concise statistical abstractions of it, temporal knowledge discovery presents significant computational and methodological challenges. However, temporal data mining embodies within it a considerable promise for the understanding of various scientific phenomena, and the potential for creation of richer and more accurate classification models, representing explicitly processes developing over a long time. An excellent survey of temporal data mining can be found in (Roddick and Spiliopoulou 2002). Enhancing the use of the temporal dimension as part of the data mining process is an emerging need in the biomedical domain (Bellazzi et al. 2011).

2.2 Temporal abstraction

Temporal abstraction (TA) is the segmentation and/or aggregation of a series of raw, time-stamped, multivariate data into a symbolic time interval series representation, often at a higher level of abstraction (e.g., instead of a series of raw Hemoglobin-value or liver-enzyme measurements, more abstract characterizations such as “3 weeks of moderate anemia”, or “5 months of decreasing liver functions”), suitable for human inspection or for data mining.

TA, which typically includes also some form of interpolation (Shahar 1999), solves several common problems in mining raw time series data, such as high variability in the sampling frequency and temporal granularity, minor measurement errors, and missing values, through the smoothing effect of the output abstractions. Thus, discovering frequent temporal patterns in multivariate temporal data can benefit from a preprocessing phase of converting the raw time-stamped data into a series of uniform symbolic time intervals. Figure 3 shows a TA process for one temporal variable.

There are several approaches to transform time point data into time intervals series; some of these exploit context-sensitive knowledge acquired from human experts, a method known as knowledge based temporal abstraction (KBTA) (Shahar 1997); others are purely automatic, and rely mostly on a discretization of the raw values and concatenation. Temporal discretization refers to the process of discretization of a time-series values, usually performed through unsupervised means, as a preprocessing step in transforming the time-stamped, raw-concept series into a set of symbolic, state-based time intervals (Azulay et al. 2007; Höppner 2002; Mörchen and Ultsch 2005; Lin et al. 2003).

Fig. 3

A series of raw time-stamped data of one concept type (at the bottom) is abstracted into an interval-based state abstraction (i.e., a value classification) that has, in this particular case, three discrete values: Low (L), Medium (M), and High (H) (in the middle); and into a gradient abstraction (i.e., the sign of the first derivative) that has the values Increasing (I), Decreasing (D), and Stable (S) (at the top)

2.3 Temporal discretization

Although the knowledge-based TA approach (Shahar 1997) is very useful for the discovery of meaningful patterns, based on a domain-specific knowledge base, especially in intensive knowledge domains such as medicine, it might be less effective when such knowledge is lacking, or when the discretization is performed not for the interpretation of the time series, but rather for the performance of other tasks, possibly less intuitive for human experts, such as classification, clustering, and prediction.

In the light of this difficulty, we can consider the option of an automated analysis of longitudinal records and the discovery of knowledge within them through an unsupervised process of discretization of the concepts’ values; indeed, it is the default option that we explore when insufficient domain knowledge exists.

Temporal discretization refers to the process of discretization of a time-series values, usually performed through unsupervised means, as a preprocessing step in transforming the time point, raw-concept series into a set of symbolic, state-based time intervals. Temporal Abstraction for time series mining in the form of time intervals was already proposed by Höppner (2002). Several common discretization methods, such as Equal Width Discretization (EWD), which uniformly divides the ranges of each value, and Equal Frequency Discretization (EFD), do not consider the temporal order of the values; other methods, such as Symbolic Aggregate approXimation (SAX) (Lin et al. 2003) (which focuses on a statistical discretization of the values) and Persist (Mörchen and Ultsch 2005) (which maximizes the duration of the resulting time intervals), explicitly consider the temporal dimension. In previous studies, we have compared several versions of these methods, especially for the purpose of discretization of time-oriented clinical data (Azulay et al. 2007) and eventually for the purpose of classification (Moskovitch and Shahar 2009).

Unlike all of the unsupervised discretization methods mentioned above, the TD4C temporal discretization method, which we introduce in this paper, determines the cutoffs for continuous, numerical variables, in a supervised fashion, driven by the ability of these cutoffs to discriminate among the target classes, based on the distribution of the abstract states resulting from the use of each cutoff, as we explain later.

In the evaluations performed in the current study, when comparing existing discretization methods to the TD4C method, we have used symbolic time intervals generated through knowledge based, and through the use of two automated unsupervised temporal discretization methods, Equal Width Discretization and SAX (Lin et al. 2003).

2.4 Mining time intervals

Mining time intervals is a relatively young research field that has mostly sprung during the past decade. Most of the methods use some subset of Allen’s temporal relations (Allen 1983), or more general disjunctions of them (Sacchi et al. 2007; Papapetrou et al. 2009; Batal et al. 2012, 2013). One of the earliest studies in the area is that of Villafane and Hua (2000), which searches for containments of time intervals in a multivariate symbolic time interval series. Kam and Fu (2000) were the first to use all of Allen’s temporal relations to compose time interval patterns, but their patterns were ambiguous, since the temporal relations among the components of a pattern are undefined, except for the temporal relations among all of the pairs of successive intervals.

Höppner (2001) was the first to define a non-ambiguous representation of time-interval patterns that are based on Allen’s relations, by a $k^{2}$ matrix, to represent all of the pair-wise relations within a k-intervals pattern. In the rest of this paper, we shall refer to a conjunction of temporal relations between pairs of intervals as a Time Intervals Related Pattern (TIRP). The formal definition of a TIRP appears in Sect. 3 (Definition 5). Papapetrou et al. (2009) proposed a hybrid approach H-DFS, which combines the first indexing the pairs of time intervals and then mining the extended TIRPs in a candidate generation fashion. Papapetrou et al. used only five temporal relations: meets, matches (equal, in terms of Allen’s relations), overlaps, contains, and follows, similar to Allen’s temporal relations, and introduced an epsilon threshold, to make the temporal relations more flexible.

ARMADA, by Winarko and Roddick (2007), is a projection-based efficient time intervals mining algorithm that uses a candidate generation and mining iterative approach. Wu and Chen (2007) proposed TPrefixSpan, which is a modification of the PrefixSpan sequential mining algorithm (Pei et al. 2001) for mining non-ambiguous temporal patterns from interval based events. Patel et al. (2008) introduced IEMiner—a method inspired by Papapetrou’s method, which extends the patterns directly, unlike Papapetrou et al.’s method; direct extension is in fact performed also in the KarmaLego method (see Sect. 3.2). Patel et al. (2008) had compared their method runtime to TPrefixSpan (Wu and Chen 2007) and H-DFS (Papapetrou et al. 2009) and found their method to be faster. More recently, Yi-Cheng et al. (2010, 2011) had presented a time intervals mining algorithm, inspired by the TPrefixSpan (Wu and Chen 2007), in which time intervals are represented by their (Start and End time) end points, and are mined using these points.

Moskovitch and Shahar (2009, 2013) introduced the KarmaLego algorithm, which performs fast time interval mining by extending TIRPs directly and by exploiting the transitivity of temporal relations to generate candidates efficiently; the KarmaLego methodology is at the basis of the KarmaLegoS classification framework presented here (Moskovitch and Shahar 2014), within which we will demonstrate the effect of the classification-driven discretization methodology. (We present the KarmaLego algorithm briefly in Sect. 3.2).

Other methods for time intervals mining were proposed, which either do not use Allen’s temporal relations (Mörchen 2006; Moskovitch et al. 2007b), or use only a subset of these relations, abstracted into a super-relation, such as Precedes, which is the disjunction of Before, Meets, Overlaps, Equal, Starts, and Finished-By, and which can form a basis for the discovery of a set of temporal association rules (Sacchi et al. 2007). Recently, Höppner and Peter (2014) had presented a language and an algorithm for mining labeled time intervals.

2.5 Classification via frequent patterns

The increased attention to the subject of mining time intervals has led several research groups to quite simultaneously propose using the discovered temporal patterns as features for classifying multivariate time series (Patel et al. 2008; Moskovitch et al. 2009; Batal et al. 2012, 2013), including the suggestion of a highly preliminary version of the KarmaLegoS framework (Moskovitch et al. 2009; Moskovitch and Shahar 2014). Interestingly, all of the studies that reported the use of temporal abstraction and time intervals mining for the purpose of classification were using datasets from the biomedical domain (Patel et al. 2008; Batal et al. 2012, 2013).

Patel et al. (2008) presented a time intervals mining algorithm, called IEMiner and used the discovered patterns for classifying multivariate time series. Patel et al. propose an entropy based measure, called GAIN, that ranks the discovered temporal patterns according to their expected contribution to the classification task. Additionally, Patel et al. propose the IEClassifier, a classification method using temporal patterns, having two versions: Best_Confidence, in which the class having the highest confidence is selected, and the Majority_Class, in which the class to which the majority of the patterns discovered belong to is selected. Batal et al. (2012, 2013) presented a study in which time intervals patterns classify multivariate time series. The authors present an apriori approach, STF-Mine, for the discovery of temporal patterns and use the $\chi ^{2}$ (chi-square) measure to select the most discriminating patterns. Batal et al.’s method was compared to a “static” implementation of the data in an evaluation on the Heparin-induced thrombocytopenia (HIT) dataset, in which the temporal approach outperformed the static implementation. Recently, Peter et al. (2013) had presented a study involving the classification of multivariate time series, using various discretization approaches. Our KarmaLegoSification framework (Moskovitch and Shahar 2014) similarly employs discovered TIRPs as features, but focuses and extends additional aspects, such as the TIRP’s representation metrics, and a smaller number of abstract temporal relations.

3 Methods

We start by introducing our classification-oriented method for discretization of multivariate data; we then explain our methodology for discovering frequent patterns given a set of symbolic intervals, which might be abstracted through any method, the KarmaLego framework, and how we extended that framework into the KarmaLegoS temporal-pattern-based classification methodology. In the next section, we present a rigorous evaluation of our discretization method in several different medical domains.

3.1 TD4C—Temporal Discretization for Classification

The supervised Temporal Discretization for Classification (TD4C) method for discretization of multivariate time series is a novel contribution and is the focus of this paper. The existing data-driven methods that were described in the background section, including EWD, EFD, SAX (Lin et al. 2003) and Persist (Mörchen and Ultsch 2005) were all unsupervised.

TD4C is a supervised learning method in which the discretization cutoffs are chosen so as to abstract the temporal data in a manner that creates the most differentiating distribution of the resulting states, amongst the entities that are classified by the various possible class values, for each of the time-oriented variables (concepts). Thus, for example, we might abstract the values of a univariate time series into three states based on their range; if there are, just for simplicity’s sake, only two outcome-class values for the time series of each entity, we would ideally like to find two cutoffs that define these three ranges, such that entities belonging to one class mostly have states from the first level (e.g., LOW) and possibly from the second level (e.g., MEDIUM), while the data of entities belonging to the other class has are mostly abstracted into states at the second level and at the third level (e.g., HIGH). Finding such a state abstraction (cutoffs) would be expected to result in the discovery of different TIRPs for each of the two outcome classes, due to a different distribution of symbolic intervals of the three state values within these TIRPs, and eventually should result in a better classification performance.

In atemporal problems, supervised discretization is often performed for classification purposes when the variables’ values are continuous, such as when generating a decision tree (Kohavi and Sahami 1996). Usually, these variables have only one value (e.g., the gender of the patient; or age when the disease is discovered). Thus, when solving these problems, supervised discretization methods are driven by the correlation of the class labels with the discrete labels. However, in the temporal domain, after state abstraction is performed, an entity (e.g., a patient) is represented, among other abstractions, by a series of symbolic (state) time intervals, which makes the supervised discretization process more complex.

We formalize here the problem of temporal discretization of time series. Given a set of ${\vert }E{\vert }$ entities classified into ${\vert }C{\vert }$ classes, having each a time-point-series $S$ to abstract into $k$ states, the task is to determine $k-1$ cutoff values.

In order to accomplish this task, a vector of probabilities representing the probabilities of the entities that belong to each class to be in each of the $k$ states over time is computed for each class. Thus, we compute a state-distribution vector $P= \langle p^{1}_{\mathrm{j}}, p^{2}_{\mathrm{j}}, \ldots p^{k}_{\mathrm{j}} \rangle$ of probabilities for each class $\hbox {C}_{\mathrm{j}}$ of the ${\vert }C{\vert }$ classes, representing the distribution of the probabilities of entities of class $j$ being in each discrete state $\hbox {S}_{\mathrm{i}}, I = 1 \ldots k$, over the whole longitudinal record, for all of the entities of Class $\hbox {C}_{\mathrm{j}}$. Thus, $p^{i}_{\mathrm{j}}$ is the probability of being in state $i$ during the total time period considered in the analysis, over all of the entities labeled by the particular class $\hbox {C}_{\mathrm{j}}$.

Thus, having ${\vert }C{\vert }$ vectors representing the distribution of the probabilities for the entities that belong to each of the ${\vert }C{\vert }$ classes, for each particular discretization option into $k$ discrete states, i.e., each particular selection of the $k-1$ cutoffs, we would like to measure the divergence among the vectors representing the classes, to determine the optimal cutoffs. To measure this divergence, we have explored three metrics: an entropy-based metric that measures the entropy of the distribution in each class vector; an Euclidean-based metric which measures the overall distance among the classes vectors, and the Kullback–Leibler divergence measure (Kullback and Leibler 1951). These three measures will determine the difference amongst the probability vectors, as described below.

3.1.1 The entropy distance measure

In the Entropy distance measure, we assess the total entropy differences amongst all of the class state-distribution vectors for the given concept, for a particular discretization, since one reason for a large difference in entropy between different class vectors might be that the given discretization is reducing the entropy of one or more of the classes, while keeping the entropy of the other classes at a uniform level.

First, the entropy of each class vector c, $\hbox {E}(c)$, is calculated as shown in Formula 1, in which $k$ is the number of states and $c$ is a class.

$$\begin{aligned} \hbox {E}(\hbox {c})= -\sum \nolimits _{\mathrm{i}=1}^\mathrm{k} \hbox {p}_\mathrm{i} \log (\hbox {p}_\mathrm{i}) \end{aligned}$$

(1)

After calculating the entropy of each class, the overall difference in entropies over all class vectors is calculated as presented in Formula 2, in which $C$ is the set of classes.

$$\begin{aligned} \hbox {EntropyDistance}= \sum \nolimits _{\mathrm{i}=1}^{\mathrm{C}-1} \sum \nolimits _{\mathrm{j}=\hbox {i}+1}^\mathrm{C} \left| {\hbox {E}\left( {\hbox {c}_\mathrm{i}}\right) -\hbox {E}\left( {\hbox {c}_\mathrm{j}}\right) }\right| \end{aligned}$$

(2)

3.1.2 The cosine distance measure

This quite intuitive, Euclidean-distance inspired measure, is based on the cosine similarity measure between vectors, as shown in Formula 3, in which the angle is computed between the two vectors (of probabilities) $v$ and $u$.

$$\begin{aligned} \hbox {Cosine}(\hbox {u, v}) = \frac{\hbox {v}\cdot \hbox {u}}{\Vert \hbox {v}\Vert \Vert \hbox {u}\Vert } \end{aligned}$$

(3)

The overall distance of the similarities is calculated by Formula 4 in radians.

$$\begin{aligned} \hbox {CosineDistance}= \sum \nolimits _{\hbox {i}=1}^{\mathrm{C}-1} \sum \nolimits _{\mathrm{j}=\hbox {i}+1}^\mathrm{C} \hbox {Cosine}(\hbox {c}_\mathrm{i}, \hbox {c}_\mathrm{j}) \end{aligned}$$

(4)

3.1.3 The Kullback–Leibler distance measure

The Kullback and Leibler (1951) divergence is a well-known measure for comparing two probability distributions, using their asymmetric relative entropy. Given two discrete probability distribution vectors P and Q of size $k: \hbox {P} = \{\hbox {p}_{1}, \hbox {p}_{2}, \ldots \hbox {p}_{k}\}$ and $\hbox {Q} = \{\hbox {q}_{1}, \hbox {q}_{2}, \ldots \hbox {q}_{k}\}$, the Kullback–Leibler divergence measure can be presented as in Formula 5. To obtain a symmetric Kullback–Leibler (SKL) measure, we computed the mean of both asymmetric relative entropy measures, i.e., in both directions, as in equation 6.

$$\begin{aligned} \hbox {KL}(\hbox {P, Q})&= \sum \nolimits _{\hbox {i}=1}^\mathrm{k} \hbox {p}_\mathrm{i} \log \left( \frac{\hbox {p}_\mathrm{i}}{\hbox {q}_\mathrm{i}}\right) \end{aligned}$$

(5)

$$\begin{aligned} \hbox {SKL(P,Q)}&= 1/2 (\hbox {KL}(\hbox {Q, P}) + \hbox {KL}(\hbox {P, Q})) \end{aligned}$$

(6)

The overall distance of the divergences is calculated by Formula 7 over all the pairs of the vectors. Note that the SKL measure is symmetric.

$$\begin{aligned} \hbox {KullbackLeiblerDistance}= \sum \nolimits _{\mathrm{i}=1}^\mathrm{c} \sum \nolimits _{\mathrm{j}=\hbox {i}+1}^\mathrm{c} \hbox {SKL}(\hbox {c}_\mathrm{i},c_\mathrm{j}) \end{aligned}$$

(7)

3.1.4 The TD4C algorithm

Determining the optimal set of cutoffs requires in theory an exhaustive search of all the possible cutoffs (i.e., $k-1$ cutoff points for $k$ bins). This is inefficient; furthermore, based on several extensive experiments that we have performed (by searching the space of all combination using a Depth First Search for $k = 3$ and $k = 4$), such an exhaustive search is not worth the effort with respect to the resulting contribution to the final classifier’s performance (Moskovitch 2011). Thus, a greedy myopic approach is used, and this is the only one we shall present here.

The first step is to obtain a set of initial candidate bins from the data, using an equal frequency binning with a large number of bins, to obtain a coarse sampling of candidate cuts in sparse regions and a fine sampling in dense regions. We used 100 bins to obtain percentiles of the data values, but a higher granularity can be used. In each iteration of the algorithm all available candidate cutoffs are individually added to the current set of cutoffs and the divergence score is calculated based on the selected cutoffs. In each step, given all of the previously chosen cutoffs, an additional cutoff achieving the highest divergence score is chosen. This is repeated until the desired number of bins is obtained through the selection of $k-1$ cutoff values.

Let $T$ be the set of time series of a temporal variable distributed within the C classes throughout all of the entities, composed of all of the series of time-stamped data points for each class, each of which includes all of the time-stamped data points of all of the entities belonging to that class. Thus, $\hbox {T} = \{t_{1,} \ldots t_{c}\}$, such that, for example, for the first class $\hbox {C}_{1}, \{t_{1} = \{\{t^{1}_{1}, t^{1}_{2}, {\ldots }t^{1}_{m(1)}\}, \{t^{2}_{1}, t^{2}_{2}, t^{2}_{m(2)}\} \ldots \{t^{n(1)}_{1}, {\ldots }t^{n(1)}_{m(n(1))}\}\}$.

Each $t_{i}$ is the collection of all the time series point values of the temporal interval that belong to all of the entities $\hbox {e}^{\mathrm{i}}_{1} \ldots \hbox {e}^{\mathrm{i}}_{\mathrm{n(i)}}$ that are members of class $c_{i}$, and the entity $j$ has $\hbox {m}(j)$ data points for that temporal variable. (To preserve clarity, we are not adding any more indices, such as for variables).

The $k-1$ cutoffs have to be determined for T. Let $V= \{v_{1}, v_{2}, \ldots v_{m}\}$ be the set of $m$ candidate value cutoffs. Let A be a state abstraction method performing the actual abstraction of the time series $T$ into the set of $k$ bins, determined by the set of cutoffs B; and let $D$ be the TD4C divergence score across all classes, for each cutoff setting.

Algorithm 1 presents the greedy approach of TD4C, in which the objective is to determine the set of cutoffs to abstract the time series $T$ with the optimal divergence score $D$ (for a given distribution distance measure DDM, such as SKL) $B$ is empty at the beginning. Then, iteratively for each potential cutoff value that is in $V$ but not in $B$ (chosen in a previous iteration), the time series $T$ is abstracted using the $A$ abstraction function into a time interval series $I$.

The temporal-abstraction distribution distance of $I$ is computed across all of the outcome classes, using the current Distance Distribution Measure (DDM), and if it is larger than the current maximal distance score $D, D$ is set to it, and the cutoff $v_{i}$ is added to $B$. Eventually, the set $B$ of the $k-1$ cutoffs that resulted in the maximal distance, according to current distribution-distance measure, is returned.

The time complexity of the TD4C method is thus $\hbox {O}(V*K*N*K*C^{2})$ or $\hbox {O}(V*K^{2}*N*C^{2})$ for $V$ (potential) cutoff values, $K$ bins, $N$ data points over all entities, and C classes. To understand this formula, note that for the KL measure, for example, one needs to multiply the main cost, namely of $\hbox {O}(V*K*N)$ of creating each set of distribution vectors (testing the discretization each time on all $\hbox {O}(N)$ points), by the cost of the KL test, i.e., by $K$ distribution bins and $C^{2}$ operations during the vector testing.

Since in practice the number of abstraction bins $K$ is a small constant, typically up to 5, and so is the number of classes $C$, and the number of different cutoff values V to be tried can be fixed as well (e.g., here $V = 100$, i.e., the value percentiles), the good news are that the TD4C algorithm is essentially of $\hbox {O}(N)$ complexity, i.e., only of linear complexity, given an input dataset of $N$ data points. The main cost is due to testing the potential discretizations through the abstraction process A. The rest of the factors are essentially constants that can be modified at will; for example, in practice, often $C=2, K=3$, and the number of cutoffs values $V$ to be considered depends on the desired value granularity and might be substantially less than 100.

The overall temporal abstraction process thus includes two main phases. First, discretization of the data into the (optimal) bins, as determined by the TD4C algorithm; and second, an iterative concatenation of all adjacent time-point states (i.e., point-based states in which one is the temporal successor of the other, given the temporal granularity at which the original input raw data were collected) having the same symbol, into time intervals (possibly extending each interval by adding to it successive time-point states of the same symbol, when relevant).

3.2 KarmaLego—fast time-intervals mining

The discovery of Time Interval Related Patterns (TIRPs) is computationally highly demanding, since it requires generating all of Allen’s seven basic temporal relations. For example, a naive generation of all TIRPs having 5 symbolic time intervals, such as in Fig. 4, with all possible temporal relations among them, requires in theory generating up to $7{^\wedge }((5^{2} - 5)/2) = 7^{10} = 282{,}475{,}249$ candidate TIRPs. In general, given a TIRP having k time intervals, we will have up to $7{^\wedge }((k^{2} - k)/2)$ candidate TIRPs.

Fig. 4

A flexible extension, using the same epsilon value, for all Allen’s seven relations, using the same Epsilon for all the relations

To overcome this difficulty, we have developed KarmaLego, a fast algorithm which generates all of the patterns efficiently by extending TIRPs directly, and exploiting the transitivity property (Freksa 1992) of the temporal relations to remove unrealistic candidates (Moskovitch and Shahar 2013).

To increase the robustness of the discovered temporal knowledge, KarmaLego uses a flexible version of Allen’s seven temporal relations. This is achieved by adding an epsilon value to all seven relations, as explained in the next section. Furthermore, we also limit the before temporal relation by a maximal allowed gap, as proposed by Winarko and Roddick (2007).

To define formally the problem of mining time intervals and relevant measures for the classification task, we first present several basic definitions. These definitions will be used in the description of the methods.

3.2.1 Definitions

To better understand the KarmaLegoS methodology, we introduce several key definitions, several of which extend our initial definitions for the KarmaLego framework (Moskovitch and Shahar 2013).

Definition 1

To define a flexible framework of Allen’s temporal relations in KarmaLego, two relations are defined on time-stamped (point-based) data, given an epsilon value.

Given two time-points $t_{1}$ and $t_{2}$:

$$\begin{aligned} t_{1}=\ ^{\varepsilon }\!t_{2}\ \textit{iff}\ {\vert }t_{2} - t_{1} \vert \le \varepsilon \end{aligned}$$

and

$$\begin{aligned} t_{1} <\ ^{\varepsilon }\!t_{2}\ \textit{iff}\ t_{2} - t_{1} > \varepsilon . \end{aligned}$$

Based on the two relations $= {\varepsilon }$ and $< {\varepsilon }$ and the epsilon value, a flexible version for all of Allen’s seven relations is defined, extending Papapetrou’s definition, as shown in Fig. 4.

The introduction of the epsilon parameter to Allen’s full set of temporal relations maintains the Jointly Exhaustive and Pairwise Disjoint (JEPD) conditions, as will be shown soon. The Jointly Exhaustive condition comes from probability theory and means that a set of events is jointly exhaustive if at least one of the events must occur. In the context of temporal relations it means that the set of temporal relations, which are defined, must cover all of the optional temporal relations among two time intervals.

The Pairwise Disjoint condition means that two sets A and B are disjoint if their intersection is the empty set. In the context of temporal relations it means that the introduction of the epsilon value as defined in Definition 1 and Fig. 4 keeps the set of the temporal relations mutually exclusive. This is indeed true, since the epsilon-extended temporal-relation definitions appearing in Fig. 4 imply that for any two time intervals, exactly one (epsilon-extended) temporal relation applies.

In addition to a flexible (epsilon-based) semantics for Allen’s seven temporal relations, we introduce a set of three abstract temporal relations (shown in Fig. 4 in grey labels): BEFORE = {before | meet} that is the disjunction of Allen’s before and meets, OVERLAP that is Allen’s overlap and CONTAIN = {finish-by | contain | start-by | equal} that is the disjunction of finish-by, contain, start-by and equal.

Definition 2

A symbolic time interval, $I = \langle s, e, sym \rangle$, is an ordered pair of time points, start-time (s) and end-time (e), and a symbol (sym) that represents one of the domain’s symbolic concepts. To make the representation uncluttered, $I.s, I.e$, and I.sym are used when the start-time, end-time, and symbol of an interval $I$ are referred to.

Definition 3

A symbolic time interval series, $IS = \{I^{1}, I^{2}, \ldots , I^{n}\}$, where each $I^{i}$ is a symbolic time interval, represents a series of symbolic time intervals, over each of which holds a start-time, end-time and a symbol.

Definition 4

A lexicographic symbolic time-interval series is a symbolic time interval series, sorted in the lexicographical order of the start-time, end-time using the relations $< {\varepsilon }, = {\varepsilon }$ and the symbols, $IS = \{I^{1}, I^{2}, \ldots , I^{n}\}$, such that:

$$\begin{aligned}&\forall I^{i},I^{j}\in IS(i<j)\wedge ((I_{.s}^i <\ ^{\varepsilon }\!I_{.s}^j )\vee (I_{.s}^i = \ ^{\varepsilon }\!I_{.s}^j \wedge I_{.e}^i < \ ^{\varepsilon }\!I_{.e}^j )\vee (I_{.s}^i = \ ^{\varepsilon }\!I_{.s}^j\\&\quad \wedge I_{.e}^i = \ ^{\varepsilon }\!I_{.e}^j \wedge I_{.sym}^i <I_{.sym}^j )) \end{aligned}$$

Since in our problem definition the time intervals are ordered lexicographically, we use only the seven temporal relations shown in Fig. 4.

Definition 5

A non-ambiguous lexicographic Time Intervals Relations Pattern (TIRP) P is defined as $P = \{I, R\}$, where $I = \{I^{1}, I^{2}, \ldots , I^{k}\}$ is a set of $k$ symbolic time intervals ordered lexicographically and

$$\begin{aligned} R&= \bigcap _{i=1}^{k-1} \bigcap _{j=i+1}^k r({I^{i},I^{j}})\\&= \left\{ r_{1,2} ({I^{1},I^{2}}), \ldots ,r_{1,k} \left( {I^{1},I^{k}}\right) ,r_{2,3} ({I^{2},I^{3}}), \ldots ,r_{k-1,k} \left( {I^{k-1},I^{k}}\right) \right\} \end{aligned}$$

defines all the temporal relations among each of the $(k^{2}-k)/2$ pairs of symbolic time intervals in $I$.

Figure 5 presents a typical TIRP, represented as a half-matrix of temporal relations. We will usually assume such a representation through the description of the KarmaLego algorithm.

One potential problem with Definition 5 is that it is purely qualitative; it ignores the precise quantitative durations of the time intervals that are the components of the TIRP. We focus on this problem, and on a possible solution of it in (Moskovitch and Shahar 2014).

Fig. 5

An example of a Time-Interval Related Pattern (TIRP), represented by a sequence of five lexicographically ordered symbolic time intervals and all of their pair-wise temporal relations. On the left, the actual five-symbols TIRP is displayed graphically, while on the right, a half matrix representation is given presenting the pairwise temporal relations between each two symbolic time intervals. Interval E is a candidate symbol that is being added to the current TIRP, and its relations with the other four symbolic intervals are shown in the last column of the half matrix

Figure 5 presents the output of a temporal interval mining process, i.e., an example of a TIRP, represented, for efficiency purposes, as a half matrix. Thus, the half matrix on the right part of Fig. 5 presents all of the pair-wise temporal relations among the TIRP’s symbolic time intervals, ordered lexicographically, that defining it in a canonical, non-ambiguous fashion. Note that half-matrix representation (as opposed to a full matrix) is possible due to the fact that each of Allen’s temporal relations has an inverse; and that the canonical aspect is due to the lexicographic ordering, which leads to a unique half matrix for each TIRP.

Definition 6

Given a database of ${\vert }E{\vert }$ distinct entities (e.g., different patients), the vertical support of a TIRP $P$ is denoted by the cardinality of the set $E^{P}$ of distinct entities within which $P$ holds at least once, divided by the total number of entities (e.g., patients) ${\vert }E{\vert }: ver\_sup(P) = {\vert }E^{P}{\vert } / {\vert }E{\vert }$. The vertical support is the term usually referred to as support in the context of association rules, itemsets, and sequential mining.

When a TIRP has vertical support above a minimal predefined threshold, it is referred to as frequent. Note that in pattern mining, such as association rules, sequential mining and time intervals mining, support typically refers to the percentage of entities in the database supporting a pattern, which is actually the vertical support presented in Definition 6.

Since a temporal pattern can be discovered multiple times within a single entity (e.g., the same TIRP appears several times (multiple instances) in the longitudinal record of the same patient), we distinguish between two types of support: the vertical support and the horizontal support, which represents the number of patterns discovered within the longitudinal record of a specific entity, as defined in definition 7.

Definition 7

The horizontal support of a TIRP $P$ for an entity $e_{i}$ (e.g., a single patient’s record), hor_sup$(\hbox {P}, e_{i})$ is the number of instances of the TIRP $P$ found in $e_{i}$. For example, the number of times that a particular temporal pattern was found in a particular patient’s record.

Definition 8

The mean horizontal support of a TIRP $P$ is the average horizontal support of all the entities $E^{P}$ supporting $P$ (i.e., for all entities that have a horizontal support $\ge 1$ for TIRP $P$).

$$\begin{aligned} MeanHorizontalSupport(P, E^{P})=\frac{\sum \limits _{i=1}^{|E^{P}|} {hor\_\sup (P, e_i)}}{|E^{P}|} \end{aligned}$$

Definition 9

The mean duration of the $n$ supporting instances of the same k-sized TIRP $P$ within an entity $e$ (e.g., within a single patient’s record; note that, per Definitions 7 and 8, an entity may have several supporting instances of a TIRP) is defined by:

$$\begin{aligned} MeanDuration(P, e)=\frac{\sum \nolimits _{i=1}^n {(Max_{j=1}^k I_e^{i, j} -I_s^{i,1})}}{n} \end{aligned}$$

where $I^{i,1}_{s}$ is the start-time (s) of the first time interval in the $i$ instance (among $n$ instances), and the Max operator selects the time interval having the latest end-time (e) among the $k$ time intervals of an instance $i$. Note that according to the lexicographical order (def 4) the first time interval must have the earliest start-time, while the latest end-time can be of any of the time intervals in the instance.

As we show Sect. 4, the horizontal support and the mean duration of TIRP are potentially useful metrics when using TIRPs as features, for classification purposes.

Definition 10

The time-intervals mining task: Given a set of entities $E$, described by a symbolic time-interval series IS, and a minimum vertical support min_ver_sup, the goal of the tasks is to find all the TIRPs whose vertical support is above the min vertical support threshold.

3.2.2 The KarmaLego algorithm

KarmaLego is a TIRP-discovery algorithm that we have defined and evaluated previously, as part of our research into effective TIRP-based classification (Moskovitch and Shahar 2014). Here, we summarize the key features of KarmaLego that are relevant to the current study. A full detailed description of KarmaLego can be found in (Moskovitch and Shahar 2014). The main body of the KarmaLego algorithm consists of two main phases, Karma and Lego (Algorithm 2).

In the first phase, referred to as Karma (Algorithm 3), all of the frequent two-sized TIRPs, $r(I_{1}, I_{2})$ having two symbolic time intervals $I_{1}$ and $I_{2}$ that are ordered lexicographically and are related by $r$, a temporal relation, are discovered, and indexed. Thus, the result of the Karma phase is the frequent symbols appearing in the first level of the enumeration tree—$\hbox {T}^{1}$, and the second level of the enumeration tree—$\hbox {T}^{2}$ containing all the frequent two-sized TIRPs, which are later extended and used by Lego for the extension process for the discovery of longer TIRPs. In the second phase, referred to as Lego (Algorithm 4), a recursive process extends the frequent 2-sized TIRPs, referred to as $\hbox {T}^{2}$, through an efficient candidate generation method (which exploits temporal transitivity) into a tree of longer frequent TIRPs. These are consisting of conjunctions of the 2-sized TIRPs that were discovered in the Karma phase. Algorithm 4 receives a tirp $t$ that is extended by any of the frequent symbols in $\hbox {T}^{1}$, and any temporal relations $r$ of the R temporal relations (in our study we had three and seven set of temporal relations) that is set among the new symbol and the last symbolic time interval. Based on the symbol and the relation $r$ a set of candidate extended TIRPs are generated efficiently, exploiting the transitivity of the temporal relations. Then for each candidate a search is performed to retrieve supporting instances that eventually results with the discovery of the enumeration tree of all the frequent TIRPs (Fig. 6).

Fig. 6

A KarmaLego enumeration tree, in which the direct expansion of TIRPs is performed. Each node represents a TIRP as a half matrix of its relevant temporal relations

Note that, for robustness purposes, we are using the flexible version of Allen’s temporal relations (see Definition 1). However, the KarmaLego algorithm is oblivious to the precise definition of temporal relations. This is demonstrated in this study, in which two sets of temporal relations are used: Allen’s original seven temporal relations and an abstract form of three temporal relations.

Modeling the complexity of a time intervals mining algorithm is not easy; similar issues are encountered when assessing the behavior of sequential mining algorithms. Thus, a rigorous empirical evaluation comparing the actual performance of the KarmaLego algorithm to existing state of the art algorithms is presented in our previous work (Moskovitch and Shahar 2013). A complexity analysis of a generic time intervals mining algorithm can be found in another of our studies (Moskovitch and Shahar 2014).

In addition, it is important to note that an analysis highlighting the need for completeness in time-interval mining algorithms is presented in detail in another of our studies, focusing on classification (Moskovitch and Shahar 2014), which is important also in the context of this study, as well as for general classification contexts. We shall briefly summarize here the key points.

KarmaLego discovers all of the frequent TIRPs of an entity (e.g., a patient record), including all of the instances of that TIRP over time within that entity. This completeness aspect enables us later to calculate the novel TIRP representations of horizontal support and mean duration.

It is important to note here that, in order to make the output of a time intervals mining algorithm such as KarmaLego complete, we must discover all of the horizontally supporting instances of a TIRP (see Definition 8). This is always the case, because we do not know ahead of time, which of the TIRP instances of size $k-1$ within a specific entity will be followed by a symbolic time interval that will (vertically) support an extended $k-$sized TIRP, and in particular, cannot assume that it will necessarily be the first instance that is discovered.

This property of the KarmaLego algorithm is different from that of typical previous TIRP discovery methods, in which the algorithm stops when discovering the first instance of a new pattern, and does not include the next one(s) in its potential considerations for extension. We consider such approaches to be erroneous, at least when the object is to find all of the TIRPs that exist within a dataset (i.e., to ensure completeness), since in general, it is impossible to know ahead of time, which instance of the pattern, for a given entity, will be (or can be) extended later to support extended TIRPs. Thus, all instances of the $k-1$ sized TIRP must be found, to ensure that if the $k$-sized TIRP exists all, it will be discovered.

For example, suppose we detect three instances of the 2-sized TIRP $<\hbox {A}$ before $\hbox {B}>$ within a given entity; we cannot know which one of them (if at all) will support the extended 3-sized TIRP, $<$(A before B) $\wedge$ (A before C) $\wedge$ (B overlaps C)$>$. For example, if only the third instance of the 2-sized TIRP is followed by a symbolic time interval C (having also the proper relations to A and B), discovering the first instance and stopping will not enable us to discover any evidence for the existence of the 3-sized TIRP within this entity, although it certainly does exist, and will decrease its overall vertical support within the overall data set.

Therefore, it is also important to note that due to this essential requirement, there is actually no additional real cost in discovering all of the instances of a given TIRP within each entity, since finding all of the instances of a given pattern for each entity is in fact obligatory, in order to ensure completeness in the discovery of all [possibly longer] TIRPs, even just for the purpose of determining whether these TIRPs exist!

3.3 KarmaLegoS—classification of multivariate time series via TIRPs

The KarmaLegoS framework for the classification of multivariate time series via TIRPs, was presented in details in (Moskovitch and Shahar 2014), includes four main components, as was shown in Fig. 2: Temporal Abstraction, Time Intervals Mining, TIRP-based Feature Representation, and Classifier induction, thus producing a TIRP-based Classifier.

Each component in the KarmaLegoS framework (see Fig. 2) has several potential settings. The temporal-abstraction method settings include the temporal-abstraction or temporal-discretization method itself (e.g. SAX, EWD, knowledge-based, TD4C) and the number of discrete states (symbols) generated. The time-intervals mining-method (i.e., KarmaLego) settings include the epsilon value and the minimal vertical threshold. The TIRP-based representation settings include the feature-selection method and the representation method of the TIRPs (a Boolean value representing an existence of the TIRP, versus actual numerical horizontal support) and the classifier-induction setting is the type of induction method used.

Before we further discuss the KarmaLegoS framework, and in particular how a single entity is classified, it is important to understand the difference between the process of TIRP-based classification and (cross) validation, and the one often used in the context of standard classification experiments.

3.3.1 Time intervals mining: the training versus the classification phases

When using TIRPs for classification purposes, an important distinction must be made between the training phase and the classification (or validation) phase. This distinction usually does not exist in the case of a standard data mining task.

First, note that when classifying static data, such as determining whether a particular geological site contains oil, commonly a static features vector, such as the type of soil and its mineral content, represents the classified entities. However, in the case of temporal classification, the entities are represented by multivariate time series, such as (in the case of clinical assessment) longitudinal, co-occurring, multiple laboratory tests, time intervals of various known diagnoses, or time intervals of various treatments, all accumulating over time. Thus, the features mostly consist of the discovered TIRPs.

Second, note as a result of the data representation nature, and the semantics of the TIRP discovery process, the features vector (consisting mostly of TIRPs), representing any particular entity, may vary according to the specific (discovered) TIRP tree that was used to represent the multivariate time series of that entity; the contents of that TIRP tree, in turn, depend on the particular entities used to generate the tree, since within each subset of entities used for the generation process, different TIRPs might pass the frequency threshold.

This insight has three major implications: (1) to the training phase, since the features (TIRPs) may be different for each training set—thus, when new entities are added to a time-oriented training set, the mining process should be applied again, using all of the entities, to produce the correct features (TIRPs), unlike the case of static classification tasks, in which the basic features (e.g., mineral content) are always the same, and are not dependent on the rest of the entities in the same class; (2) to the classification phase, since the TIRPs, once discovered using a population of entities, have to be detected (i.e., determined as existing or not) within the (longitudinal) record of a single entity, to assign, for that entity, a value to each feature; and (3) to the evaluation phase, since to perform the popular process of cross validation, in which a different portion of the dataset is used each time as a training set and the other portion is used as a testing set, the mining process that defines the very features to be used (even before the processes of feature selection and classifier induction take place) should be repeated for the particular training set used, in each iteration.

Thus, unlike the case of static data-mining tasks, in which we can use a static matrix of entities versus features, and, during the cross validation process, select each time a different subset of the feature-matrix rows (each row standing for an entity, represented by a vector of values of the same set of features), here the cross-validation process must first repeat the mining process for the selected subset of entities, extract the features (TIRPs) specific to that subset, and construct a new feature matrix for each iteration in the cross validation, before the feature-selection and learning (induction) phases.

Note that this dynamic state of affairs is qualitatively not unlike the case of text mining, in which, to construct an appropriate vector-space model, the cross validation process might involve re-computing a list of relevant terms, using measures such as term frequencies and inverse (within) document (term) frequencies (TF/IDF); but in the case of temporal classification, we encounter the issue at a significantly higher level of complexity. Note also that this observation is of course relevant to any pattern-based method for classification of multivariate time series, or, indeed, to any other data mining/machine learning task having dynamic features, that is, features that are not predefined, but rather, are defined dynamically from the training set.

We will now briefly summarize the process of training in our case. Given a set of $E$ entities divided into $C$ classes: the TD4C discretization process is performed and sets the maximal divergence cutoffs for all temporal variables (separately for each variable) within all entities that create, using some temporal abstraction procedure, a set of $K$ symbolic intervals for each entity.

The data of all of the entities are abstracted temporally using the same definitions, and the entities that are members of each class are mined, separately for each class, for TIRPs, using the same minimal vertical support threshold. The result is $C$ sets of TIRPs—each of which is related to one class. Finally, the union of all of the discovered TIRPs from each class is used for the feature-matrix representation. This set of TIRPs may include TIRPs that appear in all of the classes, or in some of them. Although the set of TIRPs can be reduced by performing feature selection, eventually there is a set of TIRPs $P$, which can be used for the training and later for classification.

Note that we do not mine the data of all of the entities set $E$ together (as a single set) for TIRPs, since certain TIRPs characterizing some of the classes might not necessarily pass the frequency threshold when diluted by entities from all other classes. Moreover, we do not necessarily desire to discover and use TIRPs that are frequent in all classes, since the resultant TIRPs in such a case will be the ones that are most common across all of the classes, which are not expected to be the ones that are in fact useful for classification purposes.

3.3.2 Classifying a single entity: the SingleKarmaLego algorithm

To classify an entity, its symbolic time intervals series must be searched for the previously discovered features within the training set, i.e., frequent TIRPs. When mining a single entity, i.e., finding all of the [frequent] TIRPs for a particular subject (e.g., a patient), the notion of minimal vertical support is meaningless, and thus, all of the relevant TIRPs existing within the record of that entity should be discovered. Moreover, in general, not all of the discovered TIRPs are relevant for the classification task: in reality, only the TIRPs that appear in the training data, and were thus defined as features, should be detected. Thus, we modified KarmaLego to be applied to a single entity, a process that we refer to as SingleKarmaLego (Moskovitch and Shahar 2014).

The SingleKarmaLego algorithm uses algorithmic methods that are not applied to multiple entities unlike KarmaLego, but that are applied to a set of time intervals of a single entity; SingleKarmaLego is very similar to KarmaLego, but instead of expanding the TIRPs that are frequent (which is meaningless in a single entity) it searches the TIRPs that were discovered in the training phase and that are given to it as input (Moskovitch and Shahar 2014). As it turns out, due to its use of the KarmaLego efficient data structures and the Karma step of indexing all pairwise interval relations within the single entity, the SingleKarmaLego algorithm has several computational advantages, relative to a naïve algorithm that simply tries to detect all of the TIRPs within the single entity’s intervals; these advantages are outside of the scope of the current discussion. However, please note that in a rigorous evaluation we had shown that it is much faster than a naïve time intervals sequential mining algorithm, especially when the maximal gap is larger and when the number of time intervals per entity is larger (Moskovitch and Shahar 2014).

Following the detection of the features (i.e., TIRPs) within the single entity, they need to be represented using one of the methods described as part of the definitions (Sect. 3.2.1), as detailed in the evaluation methods below (binary [existence], horizontal support for the TIRP within the entity, and mean duration of the pattern within the entity), and then used within a standard induction algorithm to induce a classifier.

The classifier’s performance can then be measured using various standard accuracy measures, and the dependence of that performance on the overall configuration of the process can be explicitly examined, as we describe in Sect. 4.

4 Evaluation

The main objective of the evaluation was to compare the TD4C methods to the EWD and SAX unsupervised abstraction methods, when the discovered TIRPs are used for the purpose of classifying multivariate time series. Since the KarmaLegoS framework includes quite a few potentially meaningful parameters, the number of required experiments was large.

We assumed that all interval-based temporal abstractions to be mined into frequent TIRPs will be of type STATE, and in fact, only states determined by range-value abstractions and not any arbitrary function, although additional abstractions can be generated by the KBTA method (Shahar 1997). We restricted ourselves to as to focus only on the state-generating discretization methods and directly compare these methods. Thus, our objective here was not to generate high absolute classification values, but rather to compare the relative effect of using different state-discretization methods. (We consider this aspect and our future plans to extend it, in the Discussion.)

We measured the classification performance of the resulting induced classifiers, based on the various discretization options, through the commonly used Accuracy measure (i.e., the proportion of cases in which the classification was accurate, across all of the predicted classes, out of all of the classification instances). To simplify the comparison, all output classes were binary, although we varied multiple settings, such as the number of state-abstraction bins and the number of temporal relations, as we now explain.

The evaluation included three experiments, all using the discovered TIRPs as classification features, which together answer all of the following research questions. As we discuss in Sect. 4.2 (Experimental Design), the first two experiments were designed to determine the best settings for the final, third, conclusive experiment.

The research questions posed during the three experiments were related to the TD4C methods with the varying parameters within the KarmaLegoS framework (see additional details in the descriptions of the experimental design and of the results):

• A. The core question: Which state abstraction (discretization) method is the best for classification purposes? The goal of this question was to evaluate the three TD4C methods, suggested in this paper, to the unsupervised EWD and SAX methods, and to the knowledge-based (KB) temporal-abstraction method. However, we performed that evaluation in the context of the optimal settings, determined by the other research questions.

• B. What is the best number of bins, across all discretization methods, for classification purposes? The number of bins, which is the number of states in the state abstraction, determines the level of granularity of the abstraction method. Two options were evaluated: three and four states for the various abstraction methods.

• C. Which feature selection measure, across all discretization methods, is the best for classification purposes? As part of the training phase and the tabular construction, a feature selection filter was applied, including GainRatio and GAIN with several sets of features for comparison. The first objective was to determine whether the GAIN measure Höppner 2002; Mörchen and Ultsch 2005 (Patel et al. 2008) is better than a common feature selection measure, such as GainRatio, in addition to the use of no feature selection.

• D. Since, given the features (TIRPs), we used two main classifier-induction methods representing different families of induction methods, a Random Forest classifier and a Naive-Bayes classifier, we also determined in the first experiment which method is preferable. Other methods could be included, but for the purpose of the current investigation of temporal discretization methods, we considered these two as sufficiently representative.

• E. Which set of temporal relations, across all discretization methods, is the best for classification purposes? Two sets of temporal relations were evaluated in the KarmaLegoS framework, as defined in Definition 1 in Sect. 3.2.1: the full set of Allen’s seven unique temporal relations, and a more abstract set of three temporal relations (BEFORE, OVERLAPS, CONTAINS).

• F. Which TIRP representation, across all discretization methods, is the best for classification purposes? The representation of a TIRP value for an entity in the training and test phases included three options: binary (i.e., whether the TIRP exists at least once in the record) (B), horizontal support (HS) and mean duration (MeanD).

4.1 Datasets

4.1.1 The diabetes dataset

The diabetes dataset, provided as part of collaboration with Clalit Health Services (Israel’s largest HMO) contains data on 2004 patients who have type II diabetes. The data were collected each month from 2002 to 2007. The dataset contains six concepts (laboratory values or interventions) recorded over time for each patient: hemoglobin-A1c (HbA1C) values (indicating the patient’s mean blood-glucose values over the past several months), blood glucose levels, cholesterol values, and several medications that the patients purchased: oral hypoglycemic agents (diabetic medications), cholesterol reducing statins, and beta blockers. The total amount of the diabetic medications was represented in the dataset in terms of an overall defined daily dose (DDD). Knowledge-based state-abstraction definitions for abstraction of the raw-data laboratory-test measurements into more meaningful concepts were provided by expert physicians from Ben Gurion University’s Soroka Medical Center. For the classification experiments, determining the gender of the patients was used as the classification target, since no clinical end points were provided in this particular dataset. Since there were 992 males and 1012 females, the dataset was quite balanced.

Table 1 contains the cutoff definitions used for each state in the case of the raw measurements included in the Diabetes dataset. The rest of the raw data consisted of medications, for each of which a DDD abstraction was defined.

Table 1 Laboratory-measurement data types and their cut-off (discretization) values for the knowledge-based state abstractions defined for each, in the case of the diabetes data set

4.1.2 The intensive care unit (ICU) dataset

The ICU dataset contains multivariate time series of patients who underwent cardiac surgery at the Academic Medical Center in Amsterdam, the Netherlands, between April 2002 and May 2004. Two types of data were measured: static data including details about the patient, such as age, gender, type surgery the patient underwent, whether the patient was mechanically ventilated more than 24 h during her postoperative ICU stay, and high frequency time series, measured every minute over the first 12 h of the ICU hospitalization.

The data include: mean arterial blood pressure (ABPm), central venous pressure (CVP), heart rate (HR), body temperature (TMP), and two ventilator variables, namely fraction inspired oxygen (FiO2) and level of positive end-expiratory pressure (PEEP), and low frequency time-stamped data, including base excess (BE), cardiac index (CI), creatinine kinase MB (CKMB) and glucose. For the knowledge-based state abstraction, we used the definitions of Verduijn et al. (2007). In addition, the data were abstracted with computationally unsupervised and supervised abstraction methods. (See the experimental results section).

The dataset contains 664 patients; 196 patients were mechanically ventilated for more than 24 h. 19 patients had very few values and were removed. Thus, the experimental data set included 645 patients of whom 183, or 28 %, were mechanically ventilated for more than 24 h. The main classification goal was determining if the patient needed ventilation after 24 h, given the data of the first 12 h.

4.1.3 The hepatitis dataset

The hepatitis dataset contains the results of laboratory tests performed on patients who hepatitis B or C, who were admitted to Chiba University Hospital in Japan. Hepatitis A, B, and C are viral infections that affect the liver of the patient. Hepatitis B and C chronically inflame the hepatocyte, whereas hepatitis A acutely inflames it. Hepatitis B and C are especially important, because they involve a potential risk of developing liver cirrhosis and/or carcinoma of the liver.

The dataset contained time-series data regarding laboratory tests, which were collected at Chiba University hospital in Japan. The subjects included 771 patients of hepatitis B and C who had tests performed between 1982 and 2001. The data included administrative information, such as the patient’s demographic data (age and date of birth), pathological classification of the disease, date of biopsy, result of the biopsy, and duration of interferon therapy. Additionally it included the temporal records of blood tests and urinalysis. These tests can be split into two sub-categories, in-hospital and out-hospital test data. In-hospital test data contained the results of 230 types of tests that were performed using the hospital’s equipment. Out-hospital test data contain the results of 753 types of tests, including comments of staff members, performed using special equipment at the other facilities. Consequently, the temporal data contained the results of 983 types of tests. We selected eleven variables which were found most frequent (occurring in most of the patients), including: Glutamic-Oxaloacetic Transminase (GOT), Glutamic-Pyruvic Transminase (GPT), Lactate DeHydrogenase (LDH), TP, ALkaline Phosphatase (ALP), Albumin (ALB), Total BILirubin (T-BIL), Direct BILirubin (D-BIL), Indirect BILirubin (I-BIL) and Uric Acid (UA). Many patients had a limited number of tests, so we focused only on the variables occurring frequently, which included 204 patients who had Hepatitis B and 294 patients who had Hepatitis C. No knowledge-based abstractions were available for that domain, so only automated abstraction methods were used. The objective was to classify patients as having either Hepatitis B or C.

4.2 Experimental design

The evaluation focused on the comparison of the TD4C methods to the unsupervised methods, and of the KarmaLegoS framework various parameters by performing three experiments, all using the discovered TIRPs as classification features, which together answer all of our research questions. The first two experiments are designed to determine the best settings for the final, third, conclusive experiment.

Preliminary Experiment A: Determination of the optimal number of state-abstraction bins, type of feature selection method, and, between the two classifier-induction methods we chose to use, the preferable one.

We evaluated three TD4C methods, differing by measure used to quantify the state-distribution divergence among outcome classes: Entropy, Cosine and Kullbek-Liebler; and three unsupervised state-abstraction methods: knowledge-based (KB), EWD, and SAX (research question A). The number of bins used for the automated discretization was either 3 or 4 (research question B). We also wanted to compare the GAIN measure suggested by Patel et al. (2008) to the standard GainRatio measure as a feature selection method (research question C). To be able to compare the two measures we set GAIN to 0.02, as was recommended by Patel, and used GainRatio with the same number of features. In addition, we used both measures with the same number of 100 top preferred features for comparison. We used the option of no feature selection, which we called NoFS, as a baseline. Finally, we also compared the performance of the standard classification algorithms RandomForest and Naïve Bayes (research question D).

Preliminary Experiment B: Determination of the optimal number of temporal relations and the best TIRP (feature) representation method.

The main research question here focused on the use of temporal relations (research question E): the use of Allen’s seven temporal relations versus the use of only the three abstract relations, as presented in Definition 1. In addition, we compared the two novel TIRP representations (research question F), HS and MeanD, to the default Binary (existence) representation.

Main Experiment C: Using the best settings from Preliminary Experiments A and B, and comparing all of the discretization methods.

The research question here focused on comparing the accuracy of the different discretization methods when using the optimal settings.

To answer the various research questions we ran a set of evaluation runs with 10-fold cross validation. Note that, as explained in Sect. 3.3.1, during the cross validation, in each iteration, the mining phase was repeated on the relevant data set to extract the relevant features, and the rest of the steps were performed separately. We used a 60, 40 and 60 % minimal vertical support threshold for the Hepatitis, Diabetes and ICU12h datasets respectively. Determining the minimal vertical support is an important issue, since having a low threshold will discover a larger number of TIRPs, but might require a much longer runtime. Thus, we used thresholds that will discover TIRPs for all the experimental settings and that will lead to ending the discovery process within a reasonable time.

4.3 Results

4.3.1 Experiment A: determining the optimal number of bins, feature selection method, and the preferred induction method

The first experiment focused on determining the best number of bins and comparison of the GainRatio and the GAIN feature selection measures, and the RandomForest and Naïve Bayes standard classifiers. To compare the feature selection measures we used two options: we set GAIN to 0.02, which we termed GAIN002, and used GainRatio with the same number of top selected features (as at GAIN002), which we termed GR002; and we used both measures with the top 100 selected features, which we termed GAIN100 and GR100. To generate a baseline, we ran the evaluation also without feature selection, which we termed NoFS.

To decrease the settings’ complexity and isolate the explored settings, we set the other settings to their default values: Temporal relations number: 7; Epsilon value = 0; TIRP representation = Binary; in addition to the explored settings: Bins = 3 and 4; Abstraction method = TD4C_Entropy, TD4C_Cosine, TD4C_KL, SAX, EWD, KB; Feature selection = Gain002, GR002, Gain100, GR100 and NoFS; Classifiers = Random Forest, Naïve Bayes.

Figures 7, 8, and 9 show the results of experiment 1 on each of the datasets; the mean results of all the datasets are shown in Fig. 10. In the case of the Diabetes dataset, the TD4C methods outperformed in most of the cases the unsupervised methods, although the KB method performed very well (note that the KB method can only use 3 bins, since that was the number of states defined by the expert). The TD4C_Cos was the best overall in both 3 and 4 bins, in which its performance was slightly better. The TD4C_KL method performed very well with 3 bins, but not as well when using 4 bins, while still performing better than the unsupervised methods. TD4C_Ent performed very similar for both 3 and 4 bins.

Fig. 7

In the diabetes domain, the TD4C_Cos discretization method outperformed the other methods, including KB abstraction. EWD and SAX performed worst

Fig. 8

In the ICU domain, the TD4C_KL discretization method outperformed the other methods

Fig. 9

In the Hepatitis domain, the TD4C_Ent discretization method outperformed the other methods

Fig. 10

On average, across all relevant domains and experimental settings, the TD4C discretization methods and the KB abstraction method outperformed the other methods

In the case of the ICU12h dataset, the TD4C_KL method outperformed the other methods, followed by the EWD method, whose performance using 3 bins was similar to that of the KB method. The SAX method actually led to a better classification performance than the TD4C_Ent and TD4C_KL methods, both of which performed better when using 3 bins.

In the case of the Hepatitis classification task, the TD4C_Ent method outperformed the other methods, followed by the other TD4C methods and SAX (SAX was better with 4 bins and performed less well with 3 bins). Finally, the EWD method’s performance was clear worse than that of the other methods.

The mean results, averaged across all of the datasets evaluations (Fig. 10), show that overall, the KB method’s performance was best, while the TD4C method performed very similarly to the KB method, both methods using 3 bins, and both performing better than the unsupervised methods. When using 4 bins, TD4C_Ent and TD4C_Cos performed similarly and were best, followed by TD4C_KL and SAX. Note that each result is the mean of 200 evaluation runs, due to the various runs of the two classifiers and five features selection measures, as detailed in the next results.

Figures 11, 12, 13, and 14 show the results of the classifiers and the feature selection measures of Experiment 1 on each of the datasets, and the mean results of all the datasets. In the Diabetes dataset, the Naïve Bayes classifier outperformed the Random Forest classifier. The G002 and GR002 feature selection methods seemed to perform well for the Naïve Bayes method, but poorly for the Random Forest method. In the ICU12h task, the Random Forest induction method outperformed the Naïve Bayes method, which was the case also for the Hepatitis dataset. However, the feature selection methods performed quite similarly. In the Hepatitis domain, the feature selection methods performed quite similarly when using the Random Forest, while when using the Naïve Bayes method, the GR100 and G100 feature selection methods performed better, but still not as well than as when using the Random Forest method. Again, none of the feature selection methods seemed very useful, compared to the use of no feature selection, thus making our original research question a moot one.

Fig. 11

In the diabetes domain, the Random Forest (RF) and Naïve Bayes (NB) methods performed similarly, except when using the GR002 and G002 feature-selection methods, with which the NB method performed somewhat better

Fig. 12

In the ICU domain, The Random Forest (RF) method outperformed the Naïve Bayes (NB). The feature selection methods mostly did not seem to be useful

Fig. 13

In the hepatitis domain, the Random Forest (RF) induction method outperformed the Naïve Bayes (NB) method. The feature selection methods did not seem to make much difference

Fig. 14

Mean results across all data sets and settings. The Random Forest (RF) method outperformed the Naïve Bayes (NB) method, and the feature selection methods did not seem to contribute to the results

The mean results across all the datasets show that the Random Forest induction method outperformed the Naïve Bayes method, while the feature selection methods (including the lack of such methods) performed similarly. The low effectiveness of the feature selection methods might be explained by the relatively low number of TIRPs (features) discovered originally.

4.3.2 Experiment B: determining the preferred number of temporal relations and TIRP (feature) representation method

In the second experiment, we wanted to determine the optimal temporal relations set, with respect to classification performance: Allen’s original set of seven temporal relations was compared the set of three abstract temporal relations that are proposed in Definition 1, and to evaluate the additional two TIRPs (features) representations: the HS (Definition 7) and the MeanD (Definition 9) in comparison to the default Binary representation.

The settings of this experiment were: abstraction methods: TD4C_Entropy, TD4C_Cosine, TD4C_KL, SAX, EWD, and KB; Number of Bins: 3 and 4 bins; Temporal relations: Allen’s seven relations (7) and our three abstract temporal relations (3); the epsilon value was set to 0; TIRP representation methods: HS and MeanD, in addition to the Binary representation. Given the results of experiment 1, we used here only the RandomForest classifier, which proved superior to the other induction methods, and used no feature selection (NoFS), since no clear value was demonstrated for any feature selection method.

Figures 15, 16, 17, and 18 show the effect of varying the number of temporal relations versus varying the TIRP representations. The results in the case of the Diabetes classification task show quite clearly that using three abstract relations outperformed using all seven relations for any type of TIRP representation, which in fact didn’t demonstrate any meaningful influence on the performance. In the ICU12h classification task, using three temporal abstract relations led to a better performance and the MeanD representation performed better than the Binary, MeanD were better. In the Hepatitis classification task, using the set of three abstract temporal relations was better than using the set of seven relations. The MeanD and HS representations performed better than the Binary TIRP representation;

Fig. 15

In the diabetes domain, the use of 3 temporal relations outperformed the use of 7 temporal relations; the use of the Binary (B), Horizontal Support (HS), and Mean Duration (MeanD) feature representation methods resulted in a similar performance

Fig. 16

In the ICU domain, the differences in the performance were very minor, although using 7 relations resulted in a slightly better performance when using the Binary (B) and Mean Duration (MeanD) representations, while using 3 relations was superior with the Horizontal Support (HS) method

Fig. 17

In the hepatitis domain, the use of 3 temporal relations was better than the use of 7 temporal relations, while using the MeanD representation method was somewhat better than using the other feature representation methods

Fig. 18

Mean results across all data sets and settings (in particular, discretization methods). The use of 3 temporal relations was superior to the use of 7 temporal relations; using the MeanD TIRP representation method resulted in a performance that was slightly better than when using the HS and the Binary representation methods

The mean results across all of the datasets and settings show that using three abstract temporal relations was superior to the use of seven temporal relations; and that the MeanD TIRP representation method performed somewhat better than the HS representation, which was somewhat better than the Binary representation. This observation held across all discretization methods. Thus, we conclude that the use of three abstract temporal relations is better for the purpose of classification than the use of Allen’s seven relations.

We also conclude that the use of the MeanD or the HS TIRP representations results in better performance than the use of the default Binary (existence) representation, although which of the two methods is preferable depends on the particular domain. These two measures are unique to the KarmaLego framework, which, unlike several common mining methods, discovers all of the instances of a pattern within the same entity, and doesn’t stop at the first instance discovered (thus enabling it to calculate the horizontal support and the mean duration within each entity), a capability that is enabled by its efficient candidate generation and computation. (Computing all instances of the pattern within an entity is also the sound way to compute all frequent patterns, due to the potential extension of any pattern instance into a longer one.)

4.3.3 Experiment C: Applying the optimal settings across all discretization methods

The third and main experiment compared the various abstraction methods, using the settings determined as optimal in the two preliminary experiments, and evaluated the various methods and bins. Following the previous results, we used the following settings: as abstraction methods we used TD4C_Entropy, TD4C_Cosine, TD4C_KL, KB, SAX, and EWD, with 3 and 4 bins. (Note that the knowledge-based method classifies the raw-data values into three state abstractions in the diabetes and ICU domains, thus, there are only three bins when using that method, by definition). The TIRP representation method was set to MeanD; we used NoFS—that is, no feature selection; and the induction method was Random Forest. The Epsilon value used was 0 throughout (other values did not enhance the results; see comment below).

Figures 19, 20, 21, and 22 show the results of the third experiment. Note that here each result is based on a single 10-fold cross validation run, and not on a mean of multiple settings as in the previous results. The performance of the abstraction (discretization) methods in this experiment was similar to the previous performance, in general, but here the TD4C discretization methods performed better than the KB abstraction method in some cases; overall, the TD4C methods outperformed the unsupervised methods, SAX and EWD, especially with 3 bins, as can be seen in the mean results displayed in Fig. 22.

Fig. 19

In the diabetes domain, when using 3 bins, using the EWD and SAX methods resulted in a poor performance; using the TD4C and KB methods led to much better results. When using 4 bins, the results when using the EWD method were the worst; the SAX method performed better, but the results of using the TD4C methods were much better, especially when using the Entropy and Cosine measures

Fig. 20

In the ICU domain, the results of using the TD4C_Ent were quite poor for both 3 and 4 bins, but the rest of the state abstraction methods, including the other TD4C methods, led to a similar performance, which was much better, and even superior to the performance achieved when using the KB abstraction method

Fig. 21

In the hepatitis domain, the EWD method performed poorly for both 3 and 4 bins, while using SAX lead to classification results that were quite close to the results when using the TD4C methods, which outperformed the rest. (No KB abstraction was available in this domain.)

Fig. 22

Mean results across all data sets and settings. Using the EWD method led to the poorest performance; using the SAX method was much better, but using the TD4C methods led to a superior performance, and using the KB method led to quite good results as well, when available. Using the TD4C_Cos method led to a superior performance when using either 3 or 4 bins

In the Diabetes dataset, the TD4C methods clearly outperformed the unsupervised methods, especially when using 3 bins; the TD4C methods performed very similarly to the KB method, and using the TD4C_Cos method was even slightly better. In the ICU12h dataset, most of the methods performed quite similarly, although using the TD4C_Ent resulted in a worse performance than using the other discretization methods. With 3 bins, the other TD4C methods outperformed the KB method.

However, in the case of the ICU12h task, the performance of all the methods was quite similar, except for the lower performance when using TD4C_Ent method; using the KB method resulted in slightly worse performance than using the rest of the discretization methods.

In the Hepatitis dataset, all of the TD4C methods and SAX performed quite similarly, and the EWD method’s performance was clearly worse. The mean results across all of the datasets, as displayed in Fig. 22, demonstrate that the results of using the EWD and SAX methods, when using 3 bins, were clearly worse than the results of using the TD4C methods; with 4 bins, using SAX led to better results than using the EWD, but the results of using the TD4C methods were still superior to those when using all other discretization methods, even to the results when using the KB abstraction method. It can also be seen that among the TD4C methods, the TD4C_Cos variation seemed to perform best, and was the most stable across all of the various datasets.

In addition, we performed an experiment, varying the epsilon values (starting from zero) by up to 50 time units; however, for all of the methods, increasing the size of the epsilon parameter didn’t contribute much, and in most of the cases, it actually somewhat decreased the performance, as we had discovered in a previous temporal classification study (Moskovitch and Shahar 2013).

5 Discussion and conclusions

In this study, we focus on the increasingly common use of using temporal abstraction and time intervals mining for the purpose of classification of multivariate time series (Sacchi et al. 2007; Patel et al. 2008; Moskovitch et al. 2009; Batal et al. 2012, 2013). This methodology is required especially when the time series have various representations, as illustrated in Fig. 1. Discretization, while potentially losing some information, might lead to greater generalization and thus to a better learning performance. However, this common methodology depends, among other aspects, on the particular method used for discretization of the time-oriented raw-data values into symbolic abstractions. This discretization is often performed using unsupervised methods, such as EWD and SAX, in addition to knowledge based methods, in which the cutoffs are acquired from a domain expert. Thus, for those who choose to use this increasingly used approach, we introduced in this paper the novel classification-driven TD4C temporal discretization method.

In this study, we focused only on the state abstraction, although sophisticated abstraction methods such as KBTA (Shahar 1997) can generate also much more complex abstractions (e.g., Gradient, Rate, Trend, Linear pattern, Repeating pattern), which in fact would be likely to greatly increase the absolute accuracy values in all of the settings. We also ignored any demographic data such as gender and age. We also avoided the use of any sophisticated knowledge-based interpolation methods, which constrain the gap for concatenation of points and intervals using concept—(symbol) specific and context-sensitive domain knowledge (Shahar 1999). The reason was our desire to use for classification only the temporal data, and to isolate the state-abstraction component, and in particular the common case of a range-value abstraction, which depends directly on a simple discretization of the multivariate raw data (as opposed to any arbitrarily complex function that can generate state abstractions, such as the body-mass index [BMI], which is defined as Weight/Height $\wedge 2$). Thus, we were able to compare directly and transparently the relative advantages of the different methods used for generating range-value state abstractions. In our future full-fledged classification and prediction studies, we intend to add the more complex abstractions, and also exploit atemporal variables such as Gender and Age; we then expect to obtain even higher predictive values for the overall classification process, especially in domains such as the ICU, in which trends might be at least as important as states. But our objective in the current study was not to generate high classification-accuracy values, but rather to compare the state-discretization methods in a relative fashion.

To represent the overall classification methodology in a generic fashion, and thus enable us to investigate the TD4C method and compare it to other discretization methods, we designed and implemented a comprehensive architecture and process,KarmaLegoS, for classification of multivariate time series. The KarmaLegoS framework includes a temporal-abstraction process, which can either exploit domain knowledge, when provided, or, when needed, perform on-the-fly discretization, using any provided automated-discretization method, and introduces several fundamental concepts that define the output of the time intervals mining process.

The KarmaLegoS framework uses SingleKarmaLego —an algorithm for fast TIRPs mining in a single entity that is represented by symbolic time intervals. SingleKarmaLego is used for the detection of TIRPs in the classification phase. Since in a single entity the notion of minimal vertical support is meaningless, it is performed by mining only the TIRPs that were discovered as frequent in the training set and used in the classification model.

The TD4C method is an iterative method that determines raw-data value cutoffs (for abstraction into discrete states), based on the distribution of the resulting states in the outcome set of classes, and, using one of several distribution-distance measures (Entropy, Cosine, and Kullback–Liebler), it selects the cutoffs that maximally differentiate among the distributions of the resulting states, across all classes. Note that we could also use a classic entropy-gain measure, trying to minimize the overall entropy over all classes, adjusted by the relative size of the outcome classes; we intend to experiment with such a measure in the future.

In this study, we used a greedy method to determine the optimal cutoffs; a potentially more accurate approach might be a look-ahead methodology, using breath first search. However, our experience indicates that this does not result in a better accuracy, but rather with significantly longer computational times (Moskovitch 2011).

As part of our rigorous evaluation, which was performed within three different medical domains, we have quantitatively compared the TD4C supervised method to the unsupervised discretization methods. First, we optimized the settings of the KarmaLegoS framework, including examining the use of Allen’s original seven temporal relations, versus the use of an abstract version, including only three temporal relations, which we proposed here. Note that the demonstrated effectiveness of using only three (abstract) relations greatly reduces the computational complexity of the TIRP enumeration phase in the core KarmaLego frequent TIRP-discovery algorithm, which is highly (i.e., exponentially) sensitive to the number of temporal relations.

In general, given the optimal settings, the TD4C methods usually proved superior, with respect to the resulting classification accuracy, to the unsupervised (EWD, SAX and KB) methods. When available, the KB abstraction method was, on average, quite superior to the other unsupervised methods. The KB method’s rather good performance is somewhat surprising, since it is certainly not obvious that domain experts (clinicians, in this case) necessarily define abstractions that are useful not only for their daily use, such as for interpretation and continuous monitoring, or for therapeutic (diagnostic) purposes, but also for the classification or prediction of future outcomes, or of external variables such as gender (in the case of the diabetes domain); indeed, in the case of same ICU dataset that we used, KB abstraction proved inferior, in some cases, to simple statistical abstractions (Verduijn et al. 2007). These results suggest that use of domain abstraction knowledge must always be at least considered as an option, when available. Furthermore, similarly to our observation in the beginning of this section, if one added in additional knowledge-based interval abstractions, such as Gradient, Rate, and Trend, the resulting classification accuracy might be even better. However, KB definitions are not available in each domain, especially when confronted with a new domain. As opposed to that, the TD4C methods are expected to provide a high level of accuracy in an automatic fashion, even without any prior knowledge, since they bootstrap by using the outcome classes themselves to determine the optimal cutoff values.

In a preliminary experiment of the evaluation, we have introduced and assessed two novel representation methods for temporal features (i.e., TIRPs), which exploit the capability of the KarmaLego framework to compute the number (Horizontal Support) and the mean duration (MeanD) of multiple instances of discovered TIRPs within each time-oriented record, in addition to a Binary, or Boolean (purely existential) representation, for the purpose of classification. These representation methods were shown to have an added valued, when compared to the default Binary representation method.

Note that increasing the Epsilon value beyond 0 (the default value) is in general not recommended for purposes of classification, in particular when reducing the number of temporal relations to only three (thus already increasing flexibility). This somewhat surprising result, which had been indicated by our previous classification studies (Moskovitch and Shahar 2014), was possibly due to the effect, when increasing the Epsilon value, of decreasing the number of different discovered TIRPs (although they are more frequent), by clumping together different types TIRPs, thus reducing their classification power.

This conclusion might alleviate some potential difficulties, since determining the right Epsilon value might be quite problematic and might in general require several trials for each new dataset.

Overall, when the experiments were run using the best settings, the TD4C methods were superior to the unsupervised methods (especially when compared to EWD and SAX) and slightly better than the KB method. In general, the TD4C_Cosine version was better than the other TD4C methods, and was more stable over the various datasets.

To sum up, we conclude that the use of the TD4C discretization method, when applying temporal abstraction and TIRP-based classification, as performed within the KarmaLegoS framework, can increase the resulting classification accuracy, and is potentially useful for classification and prediction tasks in time-oriented, multivariate-data domains. The use of the TD4C method might be especially valuable in new domains, in which knowledge-based definitions do not necessarily exist.

In our future work, we intend to extend the use of TD4C-like methods to the discretization of more than a single variable (i.e., determine the cut-offs of several variables simultaneously), determining the cutoff values for each temporal variable, as part of an optimization of a combination of multiple temporal variables. Furthermore, it is possible that similar methods, oriented towards the classification performance, akin to TD4C, can be used even for the discretization of the durations of the symbolic time intervals themselves, and even of the gap periods that exist between them or that are common to them, thus redefining the meaning of temporal relations in a classification-oriented fashion. Finally, we would like to further investigate semantic considerations in time intervals mining (Shknevsky et al. 2014) and move to prediction using time intervals mining (Moskovitch et al. 2014).