Skip to main content
SpringerLink
Log in

A Bilinear Pseudo-spectral Method for Solving Two-asset European and American Pricing Options

  • Published:
Computational Economics Aims and scope Submit manuscript

A Correction to this article was published on 18 May 2023

This article has been updated

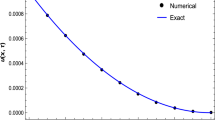
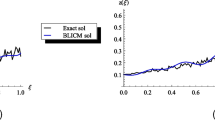
Abstract

This paper presents a bilinear Chebyshev pseudo-spectral method to compute European and American option prices under the two-asset Black–Scholes and Heston models. We expand a function and its derivatives into their Chebyshev series, so the differentiation matrices that act on the Chebyshev coefficients are sparse and better conditioned. First, the equation is spatially discretized using a bilinear pseudo-spectral method created by Chebyshev polynomials and a first–order matrix differential equation (MDE) is obtained. Then, using the Kronecker product, this equation is converted to a system of first–order ODEs. For solving the European options, by using an eigenvalue decomposition method, the arising system will be analytically solved. Therefore, the arising errors are because of spatial discretization and quadrature errors. For solving the American options, the approach is combined with the operator splitting method or penalty method to obtain the temporal discretization. By avoiding some transforms to convert the equation to a constant coefficient equation without mixed derivatives, we will obtain more accurate solutions. Also, transforming the European option into a set of separated ODEs by an eigenvalue decomposition causes to reduce the computational complexity. We also consider the hedge ratios which show the sensitivity of an option to the stock prices. Several numerical examples are included to show the accuracy and efficiency of the proposed approach. The results show that the spectral convergence can be achieved for models with smooth functions.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8

Similar content being viewed by others

Change history

References

  • Black, F., & Scholes, M. (1973). The pricing of options and corporate liabilities. Journal of Political Economy, 81(3), 637–654.

    Article  Google Scholar 

  • Černá, Dana. (2016). Numerical solution of the black-scholes equation using cubic spline wavelets. In AIP Conference Proceedings, volume 1789, page 030001. AIP Publishing LLC.

  • Chiarella, C., Griebsch, S., & Kang, B. (2014). A comparative study on time-efficient methods to price compound options in the heston model. Computers Mathematics with Applications, 67(6), 1254–1270.

    Article  Google Scholar 

  • Fasshauer, G. E., Khaliq, A. Q. M., & Voss, D. A. (2004). Using meshfree approximation for multi-asset American options. Journal of the Chinese Institute of Engineers, 27(4), 563–571.

    Article  Google Scholar 

  • Franke, Jürgen., Härdle, Wolfgang Karl., & Hafner, Christian M. (2004) Statistics of financial markets, volume 2. Springer.

  • Gaß, M., Glau, K., Mahlstedt, M., & Mair, M. (2018). Chebyshev interpolation for parametric option pricing. Finance and Stochastics, 22(3), 701–731.

    Article  Google Scholar 

  • Golbabai, A., & Nikan, O. (2020). A computational method based on the moving least-squares approach for pricing double barrier options in a time-fractional black-scholes model. Computational Economics, 55(1), 119–141.

    Article  Google Scholar 

  • Golbabai, A., Nikan, O., & Nikazad, T. (2019). Numerical analysis of time fractional Black–Scholes European option pricing model arising in financial market. Computational and Applied Mathematics, 38(4), 1–24.

    Article  Google Scholar 

  • Haentjens, T., & Hout, K. J. (2015). Adi schemes for pricing American options under the Heston model. Applied Mathematical Finance, 22(3), 207–237.

    Article  Google Scholar 

  • Heston, S. L. (1993). A closed-form solution for options with stochastic volatility with applications to bond and currency options. The review of financial studies, 6(2), 327–343.

    Article  Google Scholar 

  • Hout, K. J., & Toivanen, J. (2018). Adi schemes for valuing European options under the bates model. Applied Numerical Mathematics, 130, 143–156.

    Article  Google Scholar 

  • Hull, John C. (2022). Options futures and other derivatives. Pearson Education India.

  • Karel, IH. (2017). Numerical partial differential equations in finance explained.

  • Ikonen, S., & Toivanen, J. (2004). Operator splitting methods for American option pricing. Applied mathematics letters, 17(7), 809–814.

    Article  Google Scholar 

  • Ikonen, S., & Toivanen, J. (2009). Operator splitting methods for pricing American options under stochastic volatility. Numerische Mathematik, 113(2), 299–324.

    Article  Google Scholar 

  • Jo, J., & Kim, Y. (2013). Comparison of numerical schemes on multi-dimensional Black–Scholes equations. Bulletin of the Korean mathematical society, 50(6), 2035–2051.

    Article  Google Scholar 

  • Khan, A., Dutt, P., & Upadhyay, C. S. (2015). Nonconforming least-squares spectral element method for European options. Computers Mathematics with Applications, 70(1), 47–65.

    Article  Google Scholar 

  • Kozpınar, S., Uzunca, M., & Karasözen, B. (2020). Pricing European and American options under Heston model using discontinuous Galerkin finite elements. Mathematics and Computers in Simulation, 177, 568–587.

    Article  Google Scholar 

  • Laris, Mariano Zeron Medina., & Ruiz, Ignacio. (2018). Chebyshev methods for ultra-efficient risk calculations. arXiv preprint arXiv:1805.00898, 2018.

  • Larsson, E., Åhlander, K., & Hall, A. (2008). Multi-dimensional option pricing using radial basis functions and the generalized Fourier transform. Journal of Computational and Applied Mathematics, 222(1), 175–192.

    Article  Google Scholar 

  • Lötstedt, P., Persson, J., von Sydow, L., & Tysk, J. (2007). Space-time adaptive finite difference method for European multi-asset options. Computers Mathematics with Applications, 53(8), 1159–1180.

    Article  Google Scholar 

  • MacKenzie, Donald. (2008). An engine, not a camera: How financial models shape markets. Mit Press .

  • Margrabe, W. (1978). The value of an option to exchange one asset for another. The Journal of Finance, 33(1), 177–186.

    Article  Google Scholar 

  • Milovanović, S., & von Sydow, L. (2018). Radial basis function generated finite differences for option pricing problems. Computers Mathematics with Applications, 75(4), 1462–1481.

    Article  Google Scholar 

  • Mollapourasl, R., Fereshtian, A., & Vanmaele, M. (2019). Radial basis functions with partition of unity method for American options with stochastic volatility. Computational Economics, 53(1), 259–287.

    Article  Google Scholar 

  • Moreni, N. (2004). A variance reduction technique for American option pricing. Physica A: Statistical Mechanics and its Applications, 338(1–2), 292–295.

    Article  Google Scholar 

  • Nielsen, B. F., Skavhaug, O., & Tveito, A. (2002). Penalty and front-fixing methods for the numerical solution of American option problems. Journal of Computational Finance, 5(4), 69–98.

    Article  Google Scholar 

  • Nikan, Omid., Avazzadeh, Zakieh., & Tenreiro Machado. José A. (2021). Localized kernel-based meshless method for pricing financial options underlying fractal transmission system. Mathematical Methods in the Applied Sciences.

  • Oosterlee, C. W. (2003). On multigrid for linear complementarity problems with application to American-style options. Electronic Transactions on Numerical Analysis, 15(1), 165–185.

    Google Scholar 

  • Persson, J., & von Sydow, L. (2003). Pricing European multi-asset options using a space-time adaptive fd-method. Computing and Visualization in Science (pp. 173–83). Dept. of Information Technology: Uppsala University, Uppsala, Sweden.

    Google Scholar 

  • Putri, E. R. M., Mardianto, L., Hakam, A., Imron, C., & Susanto, H. (2021). Removing non-smoothness in solving Black–Scholes equation using a perturbation method. Physics Letters A, 402, 127367.

    Article  Google Scholar 

  • Rashidinia, J., & Khasi, M. (2019). Stable gaussian radial basis function method for solving Helmholtz equations. Computational Methods for Differential Equations, 7(1), 138–151.

    Google Scholar 

  • Rashidinia, J., Khasi, M., & Fasshauer, G. E. (2018). A stable gaussian radial basis function method for solving nonlinear unsteady convection-diffusion-reaction equations. Computers Mathematics with Applications, 75(5), 1831–1850.

    Article  Google Scholar 

  • Samadi, F., Heydari, A., & Effati, S. (2020). A numerical method based on a bilinear pseudo-spectral method to solve the convection-diffusion optimal control problems. International Journal of Computer Mathematics, 98(1), 28–46.

    Article  Google Scholar 

  • Shen, Jie., Tang, Tao., & Wang, Li-Lian. (2011). Spectral methods: algorithms, analysis and applications, volume 41. Springer Science & Business Media .

  • Teng, L., & Clevenhaus, A. (2019). Accelerated implementation of the Adi schemes for the Heston model with stochastic correlation. Journal of Computational Science, 36, 101022.

    Article  Google Scholar 

  • Ullah, M. Z. (2020). An RBF-FD sparse scheme to simulate high-dimensional Black–Scholes partial differential equations. Computers Mathematics with Applications, 79(2), 426–439.

    Article  Google Scholar 

  • Van Loan, C. F. (2000). The ubiquitous Kronecker product. Journal of computational and applied mathematics, 123(1–2), 85–100.

    Article  Google Scholar 

  • Xie, F., He, Z., & Wang, X. (2019). An importance sampling-based smoothing approach for quasi-monte Carlo simulation of discrete barrier options. European Journal of Operational Research, 274(2), 759–772.

    Article  Google Scholar 

  • Zeron, Mariano., & Ruiz, Ignacio. (2018). Dynamic initial margin via chebyshev spectral decomposition. Technical report, Technical report, Working paper (24 August).

  • Zhang, L., Lai, Y., Zhang, S., & Li, L. (2019). Efficient control variate methods with applications to exotic options pricing under subordinated Brownian motion models. The North American Journal of Economics and Finance, 47, 602–621.

    Article  Google Scholar 

  • Zhang, K., Wang, S., Yang, X., & Teol, K. L. (2009). A power penalty approach to numerical solutions of two-asset American options. Numerical Mathematics Theory Methods and Applications, 2, 202–223.

    Google Scholar 

  • Zhu, W., & Kopriva, D. A. (2009). A spectral element approximation to price European options. II. the Black-Scholes model with two underlying assets. Journal of Scientific Computing, 39, 323–39.

    Article  Google Scholar 

  • Zvan, R., Forsyth, P. A., & Vetzal, K. R. (1998). Penalty methods for American options with stochastic volatility. Journal of Computational and Applied Mathematics, 91(2), 199–218.

    Article  Google Scholar 

Download references

Funding

The authors received no financial support for this article.

Author information

Authors and Affiliations

  1. School of Mathematics, Iran University of Science and Technology, Tehran, Iran

    M. Khasi & J. Rashidinia

Authors
  1. M. Khasi
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. J. Rashidinia
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to M. Khasi.

Ethics declarations

Conflicts of interest

The authors declared no potential conflicts of interest with respect to the research of this article.

Ethical Approval

This manuscript does not contain any studies with human participants or animals performed by any of the authors.

Consent to participate

Informed consent was obtained from all individual participants included in the study.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

The original online version of this article was revised due to the symbol ≥ was updated in the equation under the heading “4.1 Solving the American option”.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Khasi, M., Rashidinia, J. A Bilinear Pseudo-spectral Method for Solving Two-asset European and American Pricing Options. Comput Econ 63, 893–918 (2024). https://doi.org/10.1007/s10614-023-10364-9

Download citation

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10614-023-10364-9

Keywords

Search

Navigation