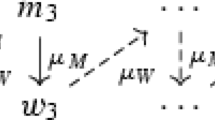Realizable Utility Maximization as a Mechanism for the Stability of Competitive General Equilibrium in a Scarf Economy

Abstract

A competitive general equilibrium (CGE) is a Pareto-optimal allocation, but it is not always stable under the mechanism of the tâtonnement process. How to drive an economy to the CGE and maintain its stability remains to be an issue with a high intellectual interest. In this article, using the celebrated counterexample of the Scarf economy, we first provide an intuitive and explicit explanation to analyze why the CGE is unstable under the tâtonnement process. Then a novel mechanism, called the realizable utility maximization mechanism (RUMM), is proposed in which the price of a product is adjusted not according to the excess demand as in the standard tâtonnement process, but according to the potential utility of the individuals owning the product. It is found that the RUMM can maintain the stability of the CGE even in the Scarf economy, and can shed light on the role of social learning in stabilizing the Scarf economy as we have learned from the literature of agent-based non-tâtonnement models.

Appendices

Appendix 1: Realizable Utility Function

Appendix 1 gives some details on the derivation of the realizable utility function, as demonstrated in Fig. 6.

1.1 Flatness

To see the flatness of $A_1$’s RU curve appearing in Fig. 6a, first notice that when $(p_1, p_2, p_3) =(x, 3,4)$, by Table 2, the the optimal bundle for $A_2$ is always $(0, \frac{3}{7}, \frac{3}{7})$, which means that $A_2$’s supply for $C_2$, $\frac{4}{7}$, is independent of x. On the other hand, the demand for $C_2$ by $A_1$ is $\frac{x}{x+3}$; clearly, $\frac{x}{x+3} \ge \frac{4}{7}$ when $x \ge 4$. In “Trading Tables” section in Appendix, we also prepare a sequence of the trading tables by allowing $p_1$ to vary from 2, to 3 (Table 5), 3.5 (Table 6), 4 (Table 7), and 5 (Table 8). By inspecting Tables 7 and 8, one can easily find that indeed the realizable utility of $A_1$ remains unchanged when $p_1$ is further increased from 4 to 5. As one can see from Table 10, in the final stage, $A_1$ still has a short of $\frac{3}{56}$ for $C_2$. With this shortage, his realizable utility remains to be $\frac{4}{7}$ = $min(\frac{5}{8}, \frac{4}{7})$, rather than $\frac{5}{8}$. The consumption complementarity with a shortage in one pertinent good ($C_2$ in this case) causes the realizable utility get flat even when $p_1 > 4$.

To see the flatness of $A_2$’s RU curve appearing in Fig. 6a, notice that $A_2$ can get $C_3$ through the route $C_2 \rightarrow C_1 \rightarrow C_3$ (getting $C_1$ first and using it as a medium to get $C_3$ at a later stage). Based on the given prices, the amount of $C_3$ that $A_2$ can acquire is just

$$\begin{aligned} C_3= \frac{4}{7} \times \frac{3}{x} \times \frac{x}{4} =\frac{3}{7}. \end{aligned}$$

Therefore, $A_2$ can acquire his optimal bundle regardless of x if $A_2$ can always sell what he wants to sell. This salability assumption depends on the demand for $C_2$ from $A_1$ and the supply of $C_3$ from $A_3$. The former is $\frac{p_1}{p_1+p_2}$, and the latter is $\frac{p_1}{p_1+p_3}.$ As we can see when $p_1$ is low, there will be no sufficient demand for $C_2$, and there will be very limited supply of $C_3$, which together indicates that $A_2$ can have difficulties getting sufficient amount of $C_3$ through the ‘medium’ $C_1$. Nevertheless, when $p_1$ is increasing, the trading easiness at both ends are enhanced, and hence the realizable utility of $A_2$ is increasing. However, this monotonicity has a limit too, which is at $p_1=3$, and can be seen from Table 6. At $p_1=3$, $A_2$ can first sell $\frac{1}{2}$ units of $C_2$ to $A_1$ to get $\frac{1}{2}$ units of $C_1$, then use this quantity of $C_1$ in exchange for $\frac{3}{8}$ units of $C_3$ from $A_3$. From Table 6, we can see that after this transaction $A_2$ is still in short of $\frac{3}{56}$ units of $C_3$, which he can acquire it by using his ‘residual’ units in $C_2$, $\frac{1}{14}$. The $\frac{3}{56}$ units of $C_3$ is futile for $A_3$ since the accompanied consumption from $C_1$ is no longer affordable. Hence, $A_2$’s optimal bundle ($C_2=C_3=\frac{3}{7}$) can be met when $p_1=3$. When $p_{1}$ is increased further up to 3.5, we basically have the same situation, except that after satisfying the demand for $C_3$ from $A_2$, $A_3$ can still have $\frac{4}{105}$ units of $C_3$ in idleness (see Table 8). When $p_{1}$ climbs to 4, $A_2$ no longer needs to do the residual trade with $A_3$; $A_2$ can sell all what he can offer to $A_1$, and he can then use the obtained $C_1$ to get enough $C_3$ from $A_3$ (See Table 9. Again, his realizable utility remain unchanged at $U_2= min(\frac{3}{7}, \frac{3}{7})= \frac{3}{7}.$

1.2 Trading Tables

In this appendix, we prepare a sequence of trading tables by allowing $p_1$ to vary from 2, to 3 (Table 6), 3.5 (Table 8), 4 (Table 9), and 5 (Table 10), while keeping $p_2=3$ and $p_3=4$. These tables are provided to facilitate the narrative analysis in the main text of Sect. 4.1.2. Each of the tables is generated in the same way as we described in Table 3 in Sect. 4.1. To derive them, one also need to refer to the optimal consumption table, such as the accompanied Table 2 seen in Sect. 4.1, under the respective set of prices. They are provided in Tables 5 ($p_1=3$), 7 ($p_1=3.5$), 11 ($p_1=4$), and 12 ($p_1=5$), respectively. Therefore, we do not intend to provide additional information here. For the use of these tables, please refer to the main text in Sect. 4.

Table 5 Demand table: $(p_1,p_2,p_3)=(3,3,4)$

Table 6 Trading table: $(p_1,p_2,p_3)= (3,3,4)$

Table 7 Demand table: $(p_1,p_2,p_3)=(3.5,3,4)$

Table 8 Trading table: $(p_1,p_2,p_3)= (3.5,3,4)$

Table 9 Trading table: $(p_1,p_2,p_3)= (4,3,4)$

Table 10 Trading table: $(p_1,p_2,p_3)= (5,3,4)$

Table 11 Demand table: $(p_1,p_2,p_3)=(4,3,4)$

Table 12 Demand table: $(p_1,p_2,p_3)=(5,3,4)$

Appendix 2: Proof of the RUMM Theorem

1.1 Proof of the RUMM Theorem 1

Proof

To facilitate the proof, it will be useful to explicitly acknowledge two lemmas. Lemma 1 is that a complete trade will not alter the excess market demand. The excess market demand for the three commodities ($f_i, i=1,2,3$), as shown in the last row of Table 1, will not be altered by a complete trade, i.e., they remain unchanged throughout the entire trading process, even though their distribution among market participants may vary with the trading process, as demonstrated in Table 3. This lemma is easily shown since a trading process is complete in the sense that all feasible trading opportunities have been exploited, and the excess market demand refers to those demands which are not feasible to satisfy given the current price setting; hence, obviously, a complete trade will not alter the excess market demand. Lemma 1, therefore, implies that at the state of the complete trade, in Regime I ($H\rightarrow L\rightarrow M \rightarrow H$), say $p_1< p_2 < p_3$, the excess market demand for the low-priced commodity ($C_1$) is positive, that for middle-priced commodity ($C_2$) is negative and that for high-priced commodity ($C_3$) is positive, and, also in Regime II ($H\rightarrow M\rightarrow L \rightarrow H$), say $p_1> p_2 > p_3$, the excess market demand for the low-priced commodity ($C_3$) is negative, that for middle-priced commodity ($C_2$) is positive and that for high-priced commodity ($C_1$) is negative.

Lemma 2 says that a positive excess market demand can only be attributed to the agent who demands this commodity but does not produce it, i.e., the consumer in the usual sense. The supplier cannot contribute to the excess market demand because his own demand has to be satisfied first before he can trade the rest that he owns, as the constrained optimization problem indicates so.¹⁶

With the above two lemmas, we can prove Theorem 1. We first prove the claims under Regime I (Theorem 1(i)), and then proceed to Regime II (Theorem 1(ii)).

(i) In Regime I, ‘$H\rightarrow L\rightarrow M \rightarrow H$’, say, $p_1< p_2 < p_3$, by Lemma 1, upon the state of the complete trade, there is an excess demand for $C_1$ and an excess supply for $C_2$. The latter implies that $A_1$’s demand for $C_2$ is fulfilled, and the former, by Lemma 2, also implies $A_1$’s own demand for $C_1$ is fulfilled; altogether, this means, upon the state of the complete trade, $A_1$ has an endowment exactly meeting his planned consumption: $e_1=\left(\frac{p_{1}} {p_1+p_2}, \frac{p_{1}} {p_1+p_2}, 0 \right)$ and $A_1$’s realizable utility is $U_1=\frac{p_{1}} {p_1+p_2}$.

Given that $C_1$ is in short, Lemma 2 says that $A_3$’s unsatisfied demand for $C_1$ is $\frac{(p_3-p_2)p_1} {(p_3+p_1)(p_1+p_2)}$. From Table 1, we already know $A_3$’s net demand for $C_1$, $d_3^1= \frac{p_3} {p_3+p_1}$. Hence, by subtracting the former from the latter, we can figure out the satisfied demand and hence the endowment of $A_3$ for $C_1$ upon the complete trade is $e_3^1=\frac{p_2} {p_1+p_2}$. Now, summing together the $C_1$ hold by $A_1$ ($e_1^1$) and the $C_1$ hold by $A_3$ ($e_3^1$), we have no $C_1$ left for $A_2$, which means $e_2^1=0$. Similarly, because $C_3$ is in short, by Lemma 2, $A_2$’s unfulfilled demand for $C_3$ is $\frac{(p_2-p_1)p_3}{(p_2+p_3)(p_3+p_1)}$; from Table 1, $d_2^3=\frac{p_2}{p_2+p_3}$. Hence, by subtracting the former from the latter, we figure out the satisfied demand of $A_2$ for $C_3$ and hence the final endowment is $e_2^3=\frac{p_1}{p_3+p_1}$. Given $e_2^1$ and $e_2^3$, $e_2^2=1-\frac{p_{3}p_{1}}{p_{2}(p_3+p_1)}$ is derived from $A_2$’s budget constraint. Hence, $e_2=(0,1-\frac{p_{3}p_{1}}{p_{2}(p_3+p_1)},\frac{p_1}{p_3+p_1})$ and $A_2$’s realizable utility is $U_2=\frac{p_1}{p_3+p_1}.$

Finally, $C_2$ has an excess supply, given $e_1^2$ and $e_2^2$, one can obtain $e_3^2=\frac{p_1^2(p_3-p_2)}{p_2(p_1+p_2)(p_3+p_1)}$; given $e_3^1$ and $e_3^2$, $e_3^3=\frac{p_3}{p_3+p_1}$ is derived from $A_3$’s budget constraint. Hence, $e_3=(\frac{p_2}{p_1+p_2}$, $\frac{p_1^2(p_3-p_2)}{p_2(p_1+p_2)(p_3+p_1)}$,$\frac{p_3}{p_3+p_1}$) and $A_3$’s realizable utility is $U_3=\frac{p_2}{p_1+p_2}$

To show that the above results generally hold for all price triples under Regime I, one simply replaces the subscript 1, 2 and 3 above with L, M and H, respectively.

(ii) In Regime II, ‘$H\rightarrow M\rightarrow L \rightarrow H$’, say $p_1> p_2 > p_3,$ by Table 1 and Lemma 1, $C_2$ is in short at the final state. By Lemma 2, we know that $A_2$’s own demand for $C_2$ is fulfilled, so $e_2^2= \frac{p_2}{p_2+p_3}$, and in the meantime the unfulfilled demand of $A_1$ for $C_2$ is $\frac{(p_1-p_3)p_2}{(p_1+p_2)(p_2+p_3)}$. From Table 1, $A_1$’s net demand for $C_2$ is $d_1^2= \frac{p_1}{p_1+p_2}$. Hence, by subtracting the former from the latter, the satisfied demand and the final endowment of $A_1$ for $C_2$ is $e_1^2=\frac{p_3}{p_2+p_3}$. Summing together the $C_2$ hold by $A_1$ ($e_1^2$) and $A_2$ ($e_2^2$), we have no $C_2$ left for $A_3$, which means $e_3^2=0$.

Since Table 1 shows that both $C_1$ and $C_3$ has an excess supply, both the demand of $A_3$ for $C_1$ and the demand of $A_2$ for $C_3$ are fulfilled, which implies that $e_3^1= d_3^1= \frac{p_3}{p_3+p_1},$ and $e_2^3= d_2^3 = \frac{p_2}{p_2+p_3}$. With the derived $e_3^1$ and $e_3^2$, $e_3^3=\frac{p_1}{p_3+p_1}$ follows from $A_3$’s budget constraint. Hence, $e_3=(\frac{p_3}{p_3+p_1},0,\frac{p_3}{p_3+p_1})$ and $A_3$’s realizable utility is $U_3=\frac{p_3}{p_3+p_1}.$ Also with derived $e_2^2$ and $e_2^3$, $e_2^1=0$ follows from $A_2$’s budget constraint. Hence, $e_2=(0,\frac{p_2}{p_2+p_3},\frac{p_2}{p_2+p_3})$ and $A_2$’s realizable utility is $U_2=\frac{p_2}{p_2+p_3}.$ Finally, with $e_2^1$ and $e_3^1$ as well as $e_2^3$ and $e_3^3$, one can figure out that $e_1^1=\frac{p_1}{p_3+p_1}$ and $e_1^3=\frac{p_{3}(p_1-p_2)}{(p_2+p_3)(p_3+p_1)}$. Hence, $e_1=(\frac{p_1}{p_3+p_1}, \frac{p_3}{p_2+p_3}, \frac{p_{3}(p_1-p_2)}{(p_2+p_3)(p_3+p_1)})$ and $A_1$’s realizable utility is $U_1=\frac{p_3}{p_2+p_3}.$

To show that the above results generally hold for all price triples under Regime II, one simply replaces the subscript 1, 2 and 3 above with H, M and L, respectively. $\square$

1.2 Proof of the RUMM Theorem 2

Fig. 7

Three “limiting” regimes

In “Proof of the RUMM Theorem 2” section in Appendix, we prove the convergence theorem of the RUMM. To facilitate our proof, we begin by introducing a few more regimes. They are required to deal with price equalities (see footnote 3). Earlier, we assumed that the three prices are unequal, but either at initialization or during the price adjustment process, equalities of prices can happen. In addition to the two regimes given in Fig. 2, three more regimes are added to handle price inequalities (Fig. 7). The three correspond to the case that the two lower prices are equal (Regime III), that the two higher prices are equal (Regime IV), and that all three are equal (Regime V). For both Regime III and IV, we give up the notation “L”, and for Regime V, we only keep the notation “H”.¹⁷ In this way, we have two prices labelled as M or H or three prices labelled as H. To distinguish them, we number them in the subscript clockwise; hence, as shown in Fig. 7, $M_1$ and $M_2$, $H_1$ and $H_2$, and $H_1$, $H_2$ and $H_3$. Accordingly, we also distinguish the agents who are endowed with the corresponding commodity by attaching the codes of the regime and the commodity to the subscript of the agent, such as $A_{III-M_1}$ and $A_{III-M_2}$, $A_{IV-H_1}$ and $A_{IV-H_2}$, and $A_{V-H_1}$, $A_{V-H_2}$, and $A_{V-H_3}$. Recall that as in Fig. 2 each arrow shows the consumer–supplier relation; the pointing ring refers to the consumer, and the pointed ring refers to the supplier. So, for example, in Regime III, $A_{III-M_1}$ produces the commodity consumed by $A_{III-H}$, and $A_{III-M_2}$ demands the commodity produced by $A_{III-H}$. Later on, when the context is clear, we shall remove the regime code and only keep the commodity code, such as simply $A_{M_1}$ and $A_{M_2}$, when Regime III as the background is clear.

Corollary 1

In the 3-agent 3-commodity Scarf economy with the initial price $p=(p_1, p_2, p_3),$ as defined in Sect. 2.1, the final endowments of the three types of agents and their realizable utilities can be determined with respect to the three price regimes as summarized in Table 13.

Proof

Corollary 1 is a result of Theorem 1, since both Regime III and Regime IV can be regarded as the ‘limiting case’ of either Regime I or Regime II by taking the limit of a price sequence of $p_{L}$ to $p_{M}$, shortly denoted by $p_L \nearrow p_M$, and further up to $p_{H}$, denoted by $p_L \nearrow p_H$. Furthermore, Regime IV can also be considered as the limiting case of Regimes I or II by taking the limit of a sequence of price of $p_M$ to $p_H$, denoted by $p_M \nearrow p_H$. Depending on the regime from which the aforementioned sequence is taken, the type of agents between two different regimes has the following correspondences.

$$\begin{aligned}&\lim _{ p_L \nearrow p_M} \{A_{\text {I}-L}, A_{\text {I}-M}, A_{\text {I}-H} \} \rightarrow \{A_{\text {III}-M_1}, A_{\text {III}-M_2}, A_{\text {III}-H} \} \end{aligned}$$

(3a)

$$\begin{aligned}&\lim _{ p_L \nearrow p_M} \{A_{\text {II}-L}, A_{\text {II}-M}, A_{\text {II}-H} \} \rightarrow \{A_{\text {III}-M_2}, A_{\text {III}-M_1}, A_{\text {III}-H} \} \end{aligned}$$

(3b)

$$\begin{aligned}&\lim _{ p_M \nearrow p_H} \{A_{\text {I}-L}, A_{\text {I}-M}, A_{\text {I}-H} \} \rightarrow \{A_{\text {IV}-M}, A_{\text {IV}-H_1}, A_{\text {IV}-H_2} \} \end{aligned}$$

(3c)

$$\begin{aligned}&\lim _{ p_M \nearrow p_H} \{A_{\text {II}-L}, A_{\text {II}-M}, A_{\text {II}-H} \} \rightarrow \{A_{\text {IV}-M}, A_{\text {IV}-H_2}, A_{\text {IV}-H_1} \} \end{aligned}$$

(3d)

With the correspondences above, one can derive the final endowment, i.e., the endowment upon the complete trade, of the three types of agents using information in Table 4. Hence, by either substituting the symbol L and M in the top panel of Table 4 with $M_1$ and $M_2$ or M and L in the bottom panel with them, one can obtain the final endowment of the agents under Regime III, as shown in the first panel of Table 13. Similarly, using the correspondence of Eqs. (3c) and (3d), one can derive the middle panel (Regime IV) of Table 13 from Table 4. Finally, we know that the equality of the three prices characterizes the competitive equilibrium, and the derivation of the final endowment under Regime V is already known from Sect. 2, Table 1. Once the final endowment is obtained, deriving the realizable utility, as shown in the last column of Table 13, is straightforward. $\square$

Table 13 Final endowment and realizable utility under Regime III, IV and V

With the additional three regimes, we can completely keep track of the price adjustment process. A price adjustment process can be viewed as a path walking in between these regimes or, alternatively, a sequence of transitions among different regimes. If these transitions follow particular rules then the entire price adjustment process can be described by a finite state automaton which identifies each regime with a state, i.e., in this case, a five-state automaton. Figure 8 is an illustration of such automaton, which will be used throughout the rest of the appendix.

On the other hand, Tables 4 and 13 together enable us to track the realizable utility of each agent and hence inform us of the gradient (marginal utility) $\frac{\partial U_i}{\partial p_i}$of each agent upon each set of prices during the entire price adjustment process. The gradient will show us the incentive of an agent to adjust the price had the agent been given a chance to do so. An example has been demonstrated in Sect. 4.1.2 (Fig. 6). A formal analysis with Fig. 8 and hence the proof of Theorem 2 is provided below.

Proof

(Theorem 2) Basically, we shall show the price adjustment process can be characterized by the five-state automaton as shown in Figure 8. To do so, we need to show how each agent, if chosen to adjust his/her price, will do so by following the realizable utility maximization principle. This is essentially to analyze the price adjustment behavior of each of the three types of agents under each regime, in other words, a total of $3\times 5$ cases. However, as we shall see, the analysis of each case is just based on Theorem 1, Corollary 1, the benevolence principle, and the gradient method. Therefore, below we shall show the cases under Regime I only.

Consider an adjustment process starting from Regime I with $p_L(0)$, $p_M(0)$ and $p_H(0)$, set by agents $A_L(0)$, $A_M(0)$ and $A_H(0)$, respectively. Assume $A_{L}(0)$ be randomly picked (Pseudocode 1, Section 1, line 8) to kick off the adjustment process. By Theorem 1, the realizable utility of the agent $A_L(0)$ or, a little cumbersome, $A_{\text {I}-L}$, is

$$\begin{aligned} U_{\text {I-L}}=\frac{p_{L}}{p_L+p_M}. \end{aligned}$$

Since

$$\begin{aligned} \frac{\partial U_{\text {I}-L}}{\partial p_L} = \frac{p_M}{(p_L+p_M)^2}>0, \end{aligned}$$

(4)

$A_{L}(0)$ has an incentive to increase the price $p_L(0)$ up to $p_M(0).$ Up to that point, the economy switch to Regime III, and the role of agent $A_{\text {I}-L}$ becomes $A_{\text {III}-M_1}$, and his/her utility, by Corollary 1, is just a constant of $\frac{1}{2}$. If $A_{\text {III}-M_1}$ continues to increase his price, the economy will switch to Regime II and his status will switch to $A_{\text {II}-M}.$ By Theorem 1,

$$\begin{aligned} U_{\text {II}-M}=\frac{p_{M}}{p_L+p_M}=\frac{p_{M}}{p_M(0)+p_M} > \frac{1}{2}, \end{aligned}$$

and

$$\begin{aligned} \frac{\partial U_{\text {II}-M}}{\partial p_M}=\frac{p_{M}(0)}{(p_M(0)+p_M)^2}>0. \end{aligned}$$

(5)

Hence, agent $A_L(0)$ will continue to increase his/her price. When $p_L(0)$ is increased up to $p_H(0)$, the economy switch to Regime IV, and $A_{L}(0)$ becomes $A_{H_2}$. By Corollary 1,

$$\begin{aligned} U_{\text {IV}-H_2}=\frac{p_{M}}{p_H+p_M}=\frac{p_{M}(0)}{p_H(0)+p_M(0)}. \end{aligned}$$

If agent $A_L(0)$ continues to increase his price, the economy will switch back to Regime I and $A_L(0)$ becomes $A_H$, according to Theorem 1,

$$\begin{aligned} U_{\text {I}-H}=\frac{p_{M}}{p_L+p_M}=\frac{p_{H}(0)}{p_M(0)+p_H(0)}, \end{aligned}$$

the same as $U_{\text {IV}-H_2}$. In the meantime, the status of $A_H(0)$ changes to $A_{\text {I}-M}$; by Theorem 1,

$$\begin{aligned} U_{\text {I}-M}=\frac{p_{L}}{p_L+p_H}=\frac{p_{M}(0)}{p_M(0)+p_H}, \end{aligned}$$

and

$$\begin{aligned} \frac{\partial U_{\text {I}-M}}{\partial p_H}=\frac{-p_{M}(0)}{(p_M(0)+p_H)^2}<0. \end{aligned}$$

(6)

By the benevolence principle the agent will not adjust his price if both $\frac{\partial U_i}{\partial p_i}=0$ and $\frac{\partial U_j}{\partial p_i}<0;$ hence, the adjustment process ends at Regime IV.

The entire price adjustment process above is illustrated by the directional link from node (regime) I to node (regime) IV in Fig. 8, and a label L side with the link denotes that this transition is driven by the utility-maximizing agent $A_{L}$ in Regime I (or $A_{\text {I}-L}$). From the analysis above, we can also notice that Regime III can switch to Regime IV driven by the agent $A_{\text {III}-M_1}$, and Regime II can switch to Regime IV driven by the agent $A_{\text {II}-M}$. These transitions are, therefore, illustrated in Figure 8 in the same manner.

Fig. 8

The finite state automaton of price adjustment processes

Now, what would it happen if the random pick goes to $A_M(0)$? By Theorem 1, in Regime I, his/her realizable utility is

$$\begin{aligned} U_{\text {I}-M}=\frac{p_{L}}{p_L+p_H}=\frac{p_{L}(0)}{p_L(0)+p_H(0)}; \end{aligned}$$

hence,

$$\begin{aligned} \frac{\partial U_{\text {I}-M}}{\partial p_M}=0. \end{aligned}$$

(7)

This shows that $A_M(0)$ has no incentive to adjust his price within Regime I. Despite so, if $A_M(0)$ reduces $p_M(0)$ down to $p_L(0)$, the state of the economy will switch to Regime III and $A_M(0)$ becomes $A_{\text {III}-M_2}.$ By Corollary 1,

$$\begin{aligned} U_{\text {III}-M_2}=\frac{p_{M}}{p_M+p_H}=\frac{p_{L}(0)}{p_L(0)+p_H(0)}, \end{aligned}$$

which is the same as the current utility $U_{\text {I}-M}$.

If $A_M(0)$ decreases $p_M(0)$ further down to be lower than $p_L(0)$, the state of the economy will switch to Regime II and $A_M(0)$ becomes $A_{\text {II}-L};$ by Theorem 1,

$$\begin{aligned} U_{\text {II}-L}=\frac{p_{L}}{p_L+p_H}=\frac{p_{L}}{p_L+p_H(0)}, \end{aligned}$$

which is an increasing function of $p_L$; this suggests that $A_M(0)$ will actually not try any price below $p_L(0)$. Hence, all the way down through Regime III to Regime II will gain $A_M(0)$ nothing. What is about the other direction?

If $A_M(0)$ adjusts $p_M(0)$ up to $p_H(0)$, the state of the economy will switch to Regime IV, and $A_M(0)$ becomes $A_{\text {IV}-H_1}$. Corollary 1 shows

$$\begin{aligned} U_{\text {IV}-H_1}=\frac{p_{M}}{p_M+p_H}=\frac{p_{L}(0)}{p_L(0)+p_H(0)}, \end{aligned}$$

which is again the same as the current utility $U_{\text {I}-M}$. If $p_{M}(0)$ is further increased beyond $p_H(0)$, the state of the economy will switch to Regime II, and $A_M(0)$ becomes $A_{H}$. By Theorem 1,

$$\begin{aligned} U_{\text {II}-H}=\frac{p_{L}}{p_L+p_M}=\frac{p_{L}(0)}{p_L(0)+p_M(0)} = U_{\text {I}-M}. \end{aligned}$$

Hence, had agent $A_M$ be picked to adjust the price, there will be no change made, and the state of the economy remains to be Regime I, which is illustrated in Fig. 8 by the link from node I to itself, with a label M aside. By the same analysis, we can show that agent $A_H$ also has no incentive to adjust $p_H(0)$, as indicated by the same link in Fig. 8.

We now have shown that if the initial state of the prices is at Regime I, it will transit to Regime IV by the actions taken by $A_L(0)$. Notice that in Fig. 8 each node gives out three links, each with their own arrowhead indicating the terminal regime. We have just shown this for Regime I. The same technique can be applied to all other initial states in other regimes, and the details are not given here.¹⁸

In this directional graph, every node has at least one route to node V but node V has no link pointing to other nodes. Hence, the regime transition driven by agents’ price adjustments eventually visit and stay at the Regime V. Hence, Regime V, the competitive equilibrium, is the terminal state of the price adjustment process. Also, we have seen that during the transition process agents either keep the price intact or adjust it up; hence the price adjustment process is upward. Furthermore, in all regimes the agents with the highest prices always keep his/her price intact; therefore, the prices converge upward to the highest of three initial prices. $\square$