Observation Driven Long Run Equilibria

Abstract

In this paper the Fractional Vector Error Correction Model (FVECM) is extended by allowing three of its parameters to vary with time: the equilibrium relationship parameter $\beta$, the variance $\sigma ^{2}$ and the cointegration degree parameter $b$. These parameters are independently updated based on the Generalized Autoregressive Score (GAS) framework. In this way three new FVECM–GAS models are created, and also the concept of ‘time-varying cointegration’ is introduced. Data from these models are simulated, and the models are compared with their fixed parameter counterparts. We show that the FVECM–GAS models perform better in the cases shown here, and thus extend the FVECM model in a useful way. We also note that an approach with fixed parameters may lead to negligence of the cointegration relationship, providing another source of errors.

1 Introduction

In general (fractional) cointegration models the equilibrium vector, denoted by $\beta$, is assumed to be constant. This means that the equilibrium relation between the variables is assumed to be constant over time. In this paper we consider the relaxation of the assumption of a constant equilibrium. Consider the prices of two identical goods in two different countries. These price series may well be related via an equilibrium relationship, but this equilibrium relationship may be subject to structural changes over time, e.g. changes in import levies or changes in the cost of transport. The question rises whether common cointegration models deal with these datasets in an appropriate way.

Another question may rise, namely what the phrase ‘relaxation of the assumption of a constant equilibrium’ means. This relaxation will lead to a time-varying equilibrium. The phrase ‘time-varying equilibrium’ may seem oxymoronic at first sight. To illustrate our desired setup, consider a large sample $S$ consisting of $N$ data points of the two-dimensional price vector introduced above. We cut the sample in two smaller samples: our first sample $S^{1}$ contains the first $n_{1}$ data points, and the other $n_{2} = N - n_{1}$ data points are in the second sample $S^{2}$. For both samples we estimate an ordinary VECM model. It may well be that we find different equilibriums for the two samples, say $\beta ^{1}$ and $\beta ^{2}$. By instead estimating only one VECM for the entire sample $S$, we may then lose important information, namely that the equilibriums for the two periods are not the same.

One can of course continue this selection of subsamples, but then questions arise: How much subsamples do we need to consider? It could be that two different equilibriums describe the dataset well, but maybe more subsamples need to be considered. And secondly, how do we determine the bounds of these subsamples? If clear structural changes have occurred somewhere in the large sample, such as an increase in import levies, one may set the cut-off point there. But if these structural changes are absent, the decision may be very difficult. And even if clear structural changes are seen, one cannot be sure that these are the only sources of a change in the equilibrium.

These notions force us to think about a model in which the equilibrium is allowed to change over time. We need to be very cautious when we use the word ‘equilibrium’. Because as we allow for updates of the equilibrium, we need to ensure that the equilibrium remains to exist. Would the change of the equilibrium be very large each period, we could of course no longer speak about a proper equilibrium. We therefore need to ensure that sufficient autocorrelation in the equilibrium series $\beta$ is present. The name that we will use for such an equilibrium, is ‘time-varying equilibrium’. So in the example above the time-varying equilibrium would be the entire series $(\beta ^{1},\dots ,\beta ^{1},\beta ^{2},\dots ,\beta ^{2})$ where $\beta ^{i}$ appears $n_{i}$ times for $i=1,2$, provided of course that enough autocorrelation is present in the series.

In order to find a suitable framework for updating $\beta$, let us consider the following three requirements. We need a framework allowing the equilibrium to change at every time $t \in \{1,2,\dots ,T\}$. Secondly, note that the size of the change in $\beta$ needs to be unrestricted as well. Finally, the development of $\beta$ needs to be—at least partly—data driven. With these three requirements, we express that both the epochs at which $\beta$ changes and also the magnitudes of these changes are unknown. The data are the only source for this information. To meet these three requirements, we construct a Fractional Vector Error Correction model (FVECM) where the vector $\beta$ is updated using the Generalized Autoregressive Score (GAS) framework from Creal et al. (2013). In the GAS framework, a parameter set is updated based on the log-likelihood value of the residuals from the previous period. This framework is very suitable in our case, since it meets all three requirements considered above.

Inspired by this approach, we consider two more FVECM–GAS models. In one model the variance $\sigma ^{2}$ is chosen to be time-varying, in the other model the cointegration degree parameter $b$ is chosen. In all cases all other parameters are assumed to be constant. It will be clear that in both cases, speaking about a time-varying equilibrium is not needed. In these two models the equilibrium will be constant, as is the case in the common FVECM model. To capture all three FVECM–GAS models in one concept, we will use the phrase ‘time-varying cointegration’ when talking about these FVECM–GAS models.

The paper is organized as follows. First in Sect. 2 we introduce the three FVECM–GAS models, after which data from these models are simulated in Sect. 3. The resulting data are evaluated, and their properties are shortly discussed. In Sect. 4 we consider how well the FVECM–GAS model can be estimated using maximum likelihood, and what the consequences will be if an incorrect model is estimated instead. Section 5 puts the models to the test on a real-world dataset, and finally Sect. 6 concludes.

2 Theoretical Setup

2.1 FVECM

A key element of the model we want to develop, is the Fractional Vector Error Correction Model (FVECM). To illustrate the concept ‘cointegration’ better, we start by considering the standard VECM model. Cointegration is an important tool in econometrics introduced by Granger (1981). The $p$-vector time series $X_{t}$ is cointegrated if $X_{t}$ is integrated of order $d$ and if there exists a full rank $p \times r$ matrix $\gamma$ such that $\gamma ' X_{t}$ is integrated of order $d-b$, with $b>0$. If this is the case, then $r$ is called the cointegration rank and $\gamma$ is the matrix with cointegration coefficients. A canonical model for standard cointegrated time series with $d=b=1$ is given by Engle and Granger (1987):

$$\begin{aligned} \Delta X_{t} = \alpha \gamma ' X_{t-1} + \varepsilon _{t}, \end{aligned}$$

(2.1)

for $t=1,\dots ,T$ with $\{\varepsilon _{t}\}_{t=1}^{T}$ independent and identically distributed (i.i.d.). Since the left hand side $\Delta X_{t}$ is stable (by definition), the right hand side will be stable as well. If the model is correctly specified, the term $\gamma ' X_{t-1}$ thus captures an equilibrium relationship between the different variables in $X_{t}$. This means that $\gamma ' X_{t-1}$ is stable, whereas $X_{t-1}$ itself is unstable.

Later we will we employ Maximum Likelihood (ML) estimation to estimate the parameters in the model. ML estimation of the standard VECM model is easy. Defining

$$\begin{aligned} y_{t} = \Delta X_{t}, \; \; \text { and } \; \; Y_{t} = (y_{1},y_{2},\dots ,y_{t}), \end{aligned}$$

and writing $\theta$ for the entire parameter vector, the log-likelihood function $L_{T}(\theta |Y_{T})$ of the entire sample $Y_{T}$ can be decomposed as follows:

$$\begin{aligned} \log L_{T}(\theta | Y_{T})&= \log p(y_{1}| \theta ) + \sum _{t=2}^{T} \; \log p(y_{t} | Y_{t-1},\theta ),\\ \text {since } \; \; L_{T}(\theta | Y_{T})&= p(Y_{T} | \theta ) = p(y_{1} | \theta ) \prod _{t=2}^{T} \; p(y_{t} | Y_{t-1} ,\theta ). \end{aligned}$$

Now we consider $p(y_{t} | Y_{t-1},\theta )$. The essential notion here is that knowledge of $Y_{t-1} = (\Delta X_{1},\Delta X_{2},\dots ,\Delta X_{t-1})$ implies knowledge of $X_{t-1}$. Since $\Delta X_{1} = X_{1}$ by definition, adding all differences up to $t-1$ implies we know $X_{t-1}$, i.e. $X_{t-1} = \sum _{1\le k < t} \Delta X_{k}$. So, $p(y_{t} | Y_{t-1},\theta ) = p(y_{t} | Y_{t-1},X_{t-1},\theta )$. In Eq. 2.1 we can see that only the information about $X_{t-1}$ is relevant in our case, so we can simplify and write $p(y_{t} | X_{t-1},\theta )$ instead of $p(y_{t} | Y_{t-1},X_{t-1},\theta )$ without losing important information.

We now assume a normal distribution for the error terms, i.e. $\varepsilon _{t} \sim N(0,\sigma ^{2})$ for $t=1,2,\dots ,T$. By definition $y_{t} = \alpha \gamma ' X_{t-1} + \varepsilon _{t}$, so the stochastic variable $(y_{t}-\alpha \beta ' X_{t-1} | X_{t-1},\theta )$ has the same distribution as the error term. Consequently, the stochastic variable $(y_{t}| X_{t-1},\theta )$ is normally distributed with mean $\mu _{t} = \alpha \gamma ' X_{t-1}$ and variance $\sigma ^{2}$. Leaving out the term $\log p(y_{1} | \theta )$ since it is non-stochastic, we thus find

$$\begin{aligned}&\log L_{T}(\theta | Y_{T}) = \sum _{t=2}^{T} -\frac{1}{2} \Bigl ( 2 \log 2 \pi + 2 \log \left| V \right| + \varepsilon _{t}' V^{-1} \varepsilon _{t} \Bigr ), \end{aligned}$$

since $\varepsilon _{t} = y_{t} - \alpha \gamma ' X_{t-1}$ by definition. Here, $V = \sigma ^{2} \cdot I_{2}$. As one can see, it is easy to construct the log-likelihood of $Y_{T} = (\Delta X_{1},\Delta X_{2},\dots ,\Delta X_{T})$ once we have assumed a normal distribution for the errors.

In the standard cointegration approach, deviations from the equilibrium are assumed to be $I(0)$. Since this assumption may often be too restrictive, in the remainder we will focus on ‘fractional cointegration’, see Johansen (2008, 2009), Johansen and Nielsen (2012), Łasak (2008, 2010). With fractional cointegration, deviations from the equilibrium can be fractionally integrated, i.e. they can be $I(d)$ for any positive $d$. These time series can be modelled via the FVECM model as presented in Granger (1986):

$$\begin{aligned} \Delta ^{d} X_{t} = \alpha \gamma ' (\Delta ^{d-b} - \Delta ^{d}) X_{t} + \varepsilon _{t}, \end{aligned}$$

(2.2)

for $t=1,\dots ,T$ with $\{\varepsilon _{t}\}_{t=1}^{T}$ i.i.d. Since the deviations are fractionally integrated, their autocorrelation function decays slower than in the standard VECM case, implying a slower rate of convergence to the equilibrium. A FVECM model is thus more general, and is able to better fit many cointegrated time series.

It is again easy to use ML estimation. Note that at time $t$ the term $(\Delta ^{d-b} - \Delta ^{d}) X_{t}$ contains history only and is known when we condition on $Y_{t-1} := (\Delta ^{d} X_{1},\Delta ^{d} X_{2},\dots ,\Delta ^{d} X_{t-1})$. This is true because one can easily perform the operation $\Delta ^{-d}$ on these elements since $d$ is a constant parameter, yielding $(X_{1}, X_{2},\dots , X_{t-1})$. From these data the term $(\Delta ^{d-b} - \Delta ^{d}) X_{t}$ can be calculated, because the present value $X_{t}$ is not contained in this term.¹ As we have seen above, conditioning on $Y_{t-1}$ is similar to conditioning on $(\Delta ^{d-b} - \Delta ^{d}) X_{t}$ in the FVECM model. If we again assume a normal distribution for the errors with mean zero and variance $\sigma ^{2}$, we thus know that $(\Delta ^{d} X_{t} | Y_{t-1})$ has a normal distribution as well with mean $\mu _{t} = \alpha \gamma ' (\Delta ^{d-b} - \Delta ^{d}) X_{t}$ and variance $\sigma ^{2}$. So also for the FVECM model, the log-likelihood is easily found. It is given by

$$\begin{aligned} \log L_{T}(\theta | Y_{T}) = \sum _{t=2}^{T} -\frac{1}{2} \Bigl ( 2 \log 2 \pi + 2 \log \left| V \right| + \varepsilon _{t}' V^{-1} \varepsilon _{t} \Bigr ), \end{aligned}$$

since now $\varepsilon _{t} = \Delta X_{t} - \alpha \beta ' (\Delta ^{d-b} - \Delta ^{d}) X_{t}$ by definition. ML estimation can again be used to find the desired parameter estimates.

2.2 GAS

GAS, the second ingredient for the FVECM–GAS model, is an acronym for Generalized Autoregressive Score, a parameter updating scheme based on the ‘score’, i.e. the derivative of the log-likelihood. It has been developed by Creal et al. (2013), see also Blasques et al. (2014a, b). Suppose we have data $Y_{t} = \{y_{1},\dots ,y_{t}\}$ for $t=1,\dots ,T$, and their distribution given by $y_{t} \sim p(y_{t} | Y_{t-1},f_{t} , \theta )$ for $t=1,\dots ,T$. Here $\theta$ is a vector containing the fixed parameters, and our goal is to update the $1$-dimensional parameter set $f_{t}$ based on the past log-likelihood value. The updating scheme for $t=1,\dots ,T-1$ is given by

$$\begin{aligned} f_{t+1} = \omega _{1} + \omega _{2} f_{t} + \omega _{3} s_{t}, \end{aligned}$$

where the ‘innovation’ $s_{t}$ is given by $s_{t} = S_{t} \cdot \nabla _{t}$ which is calculated from

$$\begin{aligned} \nabla _{t}&= \frac{\partial \log p(y_{t} | Y_{t-1},f_{t} , \theta )}{\partial f_{t}} \; \; \text { and } \; \; S_{t} = -\mathbb {E}_{t-1} \left[ \frac{\partial ^{2} \log p(y_{t} | Y_{t-1},f_{t} , \theta )}{\partial ^{2} f_{t}} \right] ^{-1}, \end{aligned}$$

or $S_{t} = 1$ if the second order derivative is not easily found. For $\omega$ we do not set parameter restrictions on beforehand, since we cannot determine in advance what the conditions will be for a stable process $\{f_{t}\}_{t=1}^{T}$ as long as $s_{t}$ is unknown. One can see that the next parameter value $f_{t+1}$ is influenced by a constant, by the present value $f_{t}$ and by a third term $s_{t}$, the value of the scaled score. If the model at time $t$ is well estimated, the score will be close to 0, implying that $f_{t}$ will not be changed much via the term $s_{t}$. If the model is not well estimated, the error may end up somewhere in the tails of the distribution. The high absolute value of $s_{t}$ will then lead to a large change in the parameter value of $f_{t}$.

The main benefit of the GAS model is that it satisfies our three requirements. One can easily see that the models allows for a change in the parameter at every epoch $t \in \{1,2,\dots ,T\}$. Also the size of a change in the parameter value is not restricted, which is an immediate consequence of the setup of the GAS model and the fact that $\omega$ is not restricted. Lastly, the model is clearly data driven. The data influence the log-likelihood which in turn influences the parameter update via $s_{t}$. These three requirements are fulfilled and state that both the size and moment of a change in the parameter $f_{t}$ is unknown to us, and that the only source of information is found in the data.

When simulating a dataset from a GAS model, the entire data set is not known in advance so we proceed recursively:

• 1. Initialize $y_{1}$ and $f_{1}$ and set $t=1$;

• 2. Calculate $f_{t+1}$ from $\nabla _{t}$ and $S_{t}$;

• 3. Simulate $y_{t+1}$ from $p(y_{t+1} | Y_{t},f_{t+1} , \theta )$;

• 4. Stop if $t=T-1$, else $t \rightarrow t+1$ and return to 2;

Using this procedure, we will simulate data from the FVECM–GAS models introduced below. When later estimating a GAS model, the maximization algorithm will proceed by maximizing the log-likelihood as described below:

• 1. Choose a parameter set $\theta$ (which includes the vector $\omega$), and set $t=1$;

• 2. Calculate the log-likelihood for time $t$ and calculate $f_{t+1}$;

• 3. If $t=T$ go to step 4, else $t \rightarrow t+1$ and return to 2;

• 4. Stop if $\log L_{T}(\theta | Y_{T})$ satisfies a maximum criterion, else return to 1 with a different $\theta$;

The algorithm we will use to find the optimal parameter set $\theta$ is ‘MaxBFGS’ from the programming language ‘Ox’, see Doornik (2007).

2.3 FVECM–GAS

As one can see, the GAS framework is very general. Having chosen a model and an error distribution, one can select a parameter set $f_{t}$ to be updated after which the model can be readily deployed. In this Section we combine the GAS framework with the FVECM model introduced above. To ease the exposition we consider a multivariate cointegrated system using the following triangular representation (see Łasak and Velasco 2015):

$$\begin{aligned} X_{t}=\left( \begin{array}{cc} I_{r} &{}\quad \beta \\ 0 &{}\quad I_{p-r} \end{array} \right) \left( \begin{array}{c} \Delta ^{b-d}\varepsilon _{0t} \\ \Delta ^{-d}\varepsilon _{1t}\\ \end{array} \right) ,\text { }t=1,\ldots ,T, \end{aligned}$$

which implies the FVECM (2.2) with $\alpha =\left( \begin{array}{c} -I_{r} \\ 0 \end{array} \right) , \gamma ^{\prime }=\left( I_{r}\ -\beta \right) \text {and } \varepsilon _{t}=(\varepsilon _{0t}',\varepsilon _{1t}')'.$

We restrict our attention to the case when $r=p-1,$ i.e. our cointegrated system is driven by a single common trend. Such situation is common in many areas of economics and finance. For example an obvious benchmark for p government bond yields y has $p-1$ cointegrating combinations, given by term spreads relative to some reference yield, e.g. $\hbox {y}_{{2}}-\hbox {y}_{{1}}, \hbox {y}_{{3}}-\mathrm{y} _{1}, \dots , \hbox {y}_{{p}}-\hbox {y}_{{1}}$, i.e. in the yield curve framework, there is only one driver of the long-run equilibria, which is the short term (instantaneous) interest rate, see Diebold (2016).

Another example would be prices of the same commodity (or stock) on different markets. A characterisation of competitive market behaviour requires all firms to set prices such that they follow a single stochastic trend, see Burke and Hunter (2007).

Moreover, the natural cointegrating combinations are almost always spreads or ratios (which of course are spreads in logs). For example, log consumption and log income may or may not be cointegrated, but if they are, then the obvious benchmark cointegrating combination is ($lnC-lnY$).

In Sect. 2.3.1 we consider the case $f_{t} = \beta _{t}$, then in Sect. 2.3.2 we focus on the case $f_{t} = \sigma ^{2}_{t}$ and finally in Sect. 2.3.3 we take $f_{t} = b_{t}$.

2.3.1 Time-Varying Beta

The FVECM and the GAS framework are now combined in order to make $\beta$ time-varying by the score-based updating scheme. In the 2-dimensional case of our interest, the vector $\beta = (\beta _{1},\beta _{2})$ is normalized by setting $\beta _{1}=1$. In order to find $\nabla _{t}$ and $S_{t}$ we thus only need to calculate the first and second derivative of the log-likelihood with respect to $\beta _{2}$. In other words, we can simplify our analysis by redefining $f_{t} = \beta _{t,2}$. Assuming $\varepsilon _{t} \sim N(0,\sigma ^{2})$ for $t=1,2,\dots ,T$, we find that $(\Delta ^{d} X_{t} | Y_{t-1},\theta )$ also has a normal distribution, namely $N(\mu _{t},\sigma ^{2})$ for $t=1,\dots ,T$, with $\mu _{t} = \alpha \beta _{t}' (\Delta ^{d-b} - \Delta ^{d}) X_{t}$. The log-likelihood is thus easily found as

$$\begin{aligned} \log L_{T}(\theta | Y_{T}) = \sum _{t=2}^{T} -\frac{1}{2} \Bigl ( 2 \log 2 \pi + 2 \log \left| V \right| + \varepsilon _{t}' V^{-1} \varepsilon _{t} \Bigr ), \end{aligned}$$

with $\varepsilon _{t} = \Delta ^{d} X_{t} - \mu _{t}$ and $V= \sigma ^{2} \cdot I_{2}$. We thus still employ the log-likelihood function from the FVECM case but now the error term is different since it includes the time-varying component $\beta _{t}$. Of course, at each fixed moment $t$ this is just a fixed value, so our analysis is almost unchanged. In order to find the GAS-term $s_{t}$ we derive the summand once and twice with respect to $\beta _{t}$, yielding

$$\begin{aligned} \nabla _{t}&= - \left[ \alpha V^{-1} \left( (\Delta ^{d} X_{t} + 2 \beta _{t,2} \alpha ) (\Delta ^{d-b} - \Delta ^{d}) X_{t,2} \right. \right. \\&\quad \left. \left. -\, \alpha (\Delta ^{d-b} - \Delta ^{d}) X_{t,1} \right) (\Delta ^{d-b} - \Delta ^{d}) X_{t,2} \right] ,\\ S_{t}&= -\,\mathbb {E}_{t} \left[ - \alpha ' V^{-1} \alpha (\Delta ^{d-b} - \Delta ^{d}) X_{t,2}^{2} \right] ^{-1} = \left[ \alpha ' V^{-1} \alpha (\Delta ^{d-b} - \Delta ^{d}) X_{t,2}^{2} \right] ^{-1}. \end{aligned}$$

With $s_{t} = S_{t} \cdot \nabla _{t}$ we can now construct the the FVECM–GAS model for updating $\beta _{t}$:

$$\begin{aligned} \Delta ^{d} X_{t}&= \alpha \beta _{t}' (\Delta ^{d-b} - \Delta ^{d}) X_{t} + \varepsilon _{t},\\ \beta _{t+1,2}&= \omega _{1} + \omega _{2} \beta _{t,2} + \omega _{3} s_{t}. \end{aligned}$$

for $t = 1,\dots ,T$ and $\beta _{1,2} = \beta _{init}$ for some (possibly stochastic) initialization $\beta _{init}$.

An interpretation for the time-varying $\beta$ coefficient can be given by taking a closer look at the equilibrium relationship between the variables. Consider the following example, where prices of a certain good in two different locations $A$ and $B$ are observed. The equilibrium price relation at some point in time is given by $p_{A} = \beta \cdot p_{B}$, for some $\beta > 0$. If these locations are very close, one can expect $\beta = 1$ since people’s choice of the cheaper product will equate the two prices. Now suppose instead that the locations are far apart, e.g. they are in two different countries. The good is produced in country $A$ and sold both in country $A$ and $B$, probably implying $\beta < 1$. Assume that $\beta = 0.8$. This $\beta$ may be the result of many factors, mainly economic and geographic. If country $B$ decreases its import levies, $\beta$ may decrease towards 0.6. Or if cheaper transport is available due to new ways of transport or due to decreasing fuel prices, $\beta$ may increase towards 0.9.

Of course, more examples can be given where equilibrium relationships between variables are possibly changing over time. If this is not recognized and instead a FVECM with constant $\beta$ is estimated, one may conclude that the variables are not cointegrated since too many deviations from the ‘presumed equilibrium’ are encountered. In fact, this may just be the result of misspecification instead of absence of cointegration. We will encounter such a case in Fig. 5 in Sect. 3.1.2. As is commonly known, interference based on misspecified models can be harmful. If then also the variables are in fact cointegrated, the double misspecification may lead to considerably erroneous results.

As stated earlier, we have to think carefully about the meaning and interpretation of this model. Since $\beta$ expresses an equilibrium relationship between the two variables in $X_{t}$, the model above introduces the concept of a time-varying equilibrium. However, we can only speak about a proper equilibrium, if enough correlation between the $\beta$’s is seen. If $\beta$ is changing very much each period, maybe the existence of an equilibrium is not plausible. As a consequence, it may be the case that the variables in $X_{t}$ are not cointegrated at all. Therefore, when performing simulation and estimation with this model, we need to consider the correlation in the $\beta$ series. At this moment however, we do not give explicit conditions for the existence of a time-varying equilibrium and time-varying cointegration. Instead, in Sect. 3 we will consider some simulations from this model, after which we can make a more precise statement about time-varying equilibriums and the concept of time-varying cointegration.

2.3.2 Time-Varying Variance

Another appealing option is to vary the variance. We choose $f_{t} = \sigma ^{2}_{t}$ and to ensure a positive variance, we now assume $\varepsilon _{t} \sim N(0,e^{\sigma _{t}^{2}})$. So in fact we make the log-variance of the error terms time-varying. We then find that at each moment in time $t$, $(\Delta ^{d} X_{t} | Y_{t-1},\theta ) \sim N(\mu _{t},e^{\sigma _{t}^{2}})$ for $t=1,\dots ,T$, with $\mu _{t} = \alpha \beta ' (\Delta ^{d-b} - \Delta ^{d}) X_{t}$. The log-likelihood then yields

$$\begin{aligned} \log L_{T}(\theta | Y_{T}) = \sum _{t=2}^{T} -\frac{1}{2} \Bigl ( 2 \log 2 \pi + 2 \log \left| V \right| + \varepsilon _{t}' V^{-1} \varepsilon _{t} \Bigr ), \end{aligned}$$

with $V = e^{\sigma _{t}^{2}} \cdot I_{2}$. Deriving the summand at time $t$ log-likelihood twice with respect to $\sigma _{t}^{2}$, we arrive at the following FVECM–GAS model:

$$\begin{aligned} \Delta ^{d} X_{t}&= \alpha \beta ' (\Delta ^{d-b} - \Delta ^{d}) X_{t} + \varepsilon _{t},\\ \sigma ^{2}_{t+1}&= \omega _{1} + \omega _{2} \sigma ^{2}_{t} + \omega _{3} s_{t}. \end{aligned}$$

with $\nabla _{t} = - 1 + (1/2) e^{-\sigma _{t}^{2}} \cdot \varepsilon _{t}' \varepsilon _{t}$ and $S_{t} = \left( (1/2) e^{-\sigma _{t}^{2}} \cdot \varepsilon _{t}' \varepsilon _{t} \right) ^{-1}$ for $t = 1,\dots ,T$ and $\sigma ^{2}_{1} = \sigma ^{2}_{init}$ for some (possibly stochastic) initialization $\sigma ^{2}_{init}$.

In the model introduced here, we do not have a time-varying equilibrium. The equilibrium in this case is constant just as in the ordinary FVECM case. So, what can be the benefit of such a model? Often, in economic time series, clusters of volatility² are present. Especially when a crisis occurs, periods with high volatility are seen. Afterwards, the volatility may slowly decay towards pre-crisis levels. Also structural changes such as increasing market regulation or decreasing liquidity may lead to a downward pattern in volatility. In both cases the magnitude of the shocks $\varepsilon _{t}$ will change throughout time. If this is not well modelled, one may overlook the presence of cointegration, or have difficulties in trying to estimate the correct parameters. In such cases, the model introduced here may provide a better specification.

2.3.3 Time-Varying b

In the final case we consider the parameter $b$, representing the cointegration degree. Since $b$ needs to be restricted to non-negative values, we again slightly adapt the original model and restate it as:

$$\begin{aligned} \Delta ^{d} X_{t}&= \alpha \beta ' \left( \Delta ^{d-e^{b_{t}}} - \Delta ^{d}\right) X_{t} + \varepsilon _{t},\\ b_{t+1}&= \omega _{1} + \omega _{2} b_{t} + \omega _{3} s_{t},\\ s_{t}&= S_{t} \cdot \nabla _{t}. \end{aligned}$$

for $t = 1,\dots ,T$ and $b_{1} = b_{init}$ for some (possibly stochastic) initialization $b_{init}$. Now we know that at each moment in time $t$, $(\Delta ^{d} X_{t} | Y_{t-1},\theta ) \sim N(\mu _{t},\sigma ^{2})$ for $t=1,\dots ,T$, with $\mu _{t} = \alpha \beta ' (\Delta ^{d-e^{b_{t}}} - \Delta ^{d}) X_{t}$. The log-likelihood in this case is

$$\begin{aligned} \log L_{T}(\theta | Y_{T}) = \sum _{t=2}^{T} -\frac{1}{2} \Bigl ( 2 \log 2 \pi + 2 \log \left| V \right| + \varepsilon _{t}' V^{-1} \varepsilon _{t} \Bigr ), \end{aligned}$$

but now with $\varepsilon _{t} = \Delta ^{d} X_{t} - \alpha \beta ' (\Delta ^{d-e^{b_{t}}} - \Delta ^{d}) X_{t}$ and $V= \sigma ^{2} \cdot I_{2}$. We derive the summand with respect to $b$ once and twice, yielding

$$\begin{aligned} \nabla _{t}&= - V^{-1} \left( \Delta ^{d} X_{t} - \alpha \beta ' (\Delta ^{d-e^{b_{t}}} - \Delta ^{d}) X_{t} \right) \cdot \alpha \beta ' \left( \bar{\Delta }^{d-e^{b_{t}}} X_{t} \right) e^{b_{t}}. \end{aligned}$$

Here, $\bar{\Delta } = \frac{d}{d k} \Delta ^{k}$ i.e. the derivative of the difference operator with respect to the difference degree. For $S_{t}$ we take the identity matrix since deriving the log-likelihood twice with respect to $b$ is cumbersome due to the $e^{b}$ term involved. If the model at some point is correctly specified, we know that $\beta ' X_{t}$ is an $I(d-e^{b})$ time series. The parameter $b$ therefore influences the degree to which $\beta ' X_{t}$ is integrated. Restated, $b$ influences the memory in the series $\beta ' X_{t}$, i.e. $b$ determines at which speed the variables in $\beta ' X_{t}$ converge to their equilibriums.

In this model we again do not have a time-varying equilibrium. Only the speed of convergence towards the equilibrium is varied. Data resulting from this model will be indicated as ‘time-varying cointegrated’. The fact that $b$ is time-varying may have large implications for the cointegration relationship. Suppose that $b$ is very small for some time, then $e^{b}$ will be almost zero, implying that the variables in $X$ are not cointegrated at all for some period. Therefore, we need to carefully investigate how $b$ evolves, to ensure that the model remains a cointegration model.

One possible interpretation (among others) is that $b$ relates to atomicity in a market. Let us take up the example of a good with prices $p_{A}$ and $p_{B}$ in country $A$ and $B$ respectively. The relationship between the prices is expressed as $p_{A} = \beta \cdot p_{B}$. Take for ease $\beta =1$ and $d=0.9$. If many economic actors are available in the market and trading is inexpensive, deviations from the equilibrium will be noticed early and prices will quickly return to their equilibrium. This is reflected by $e^{b} \approx d$. In case some actors have quit the market or if trading—due to some barriers—is more difficult, return to the equilibrium may take more time. The latter can be captured by for example $b=\log (0.3)$.

More examples with varying parameters $\beta$, $\sigma ^{2}$ and $b$ can be given. The benefit from these models not only needs to be illustrated by examples, but has to result from putting the model to the test on a simulated or real-world dataset. In the next Section we therefore simulate datasets from all three models, and explore their benefits in more detail.

3 Simulating Data

In this Section, we simulate and describe a few two dimesional systems using the three FVECM–GAS models introduced above. Hereby we illustrate which datasets can be generated by the model, but it also allows us to evaluate the usefulness of the FVECM–GAS models. We focus on the vector $\omega$, although less on $\omega _{1}$ since this parameter only affects the level. By choosing many different values for $\omega _{2}$ and $\omega _{3}$, the capabilities and benefits of the models will be best shown. Below we only state the chosen values for $\omega$. The entire parameterization can be found in the Appendix (Sect. 7).

As we will see, many different paths for $\beta$, $\sigma ^{2}$ and $b$ can be created with the FVECM–GAS model. Therefore we will each time perform the Johansen ‘maximum eigenvalue’ test for cointegration on the simulated data with $\alpha = 5\%$, to see whether they are cointegrated. Here of course we mean cointegrated in the ordinary meaning of the word, so not time-varying cointegration.

3.1 Time-Varying Beta

3.1.1 Deterministic

The GAS-VECM model can capture simple linear and hyperbolic patterns of the series $\beta := \{\beta _{1},\dots ,\beta _{T}\}$ by choosing $\omega _{3} = 0$. In that case the model for $\beta$ is reduced to a simple AR model without disturbances. An example is given in Fig. 1, for $\omega = (0.1, 0.89 , 0)$.

Fig. 1

Simulated series from the FVECM–GAS model with beta hyperbolically decaying towards the value 10/11

Every period, $\beta$ is reduced by a small amount, and hyperbolically decays towards $0.1/(1-0.89) = 10/11 \approx 0.909$. This model can thus account for deterministic development of $\beta$, both in a linear and hyperbolic fashion. By the Johansen test, the variables $y_{1}$ and $y_{2}$ are cointegrated with rank 1. Depending on the choice of $\omega$ one either has a linear or a hyperbolic pattern of $\beta$. In the first case $\beta$ will not converge if $\omega _{1} \ne 0$. Instead, the series will follow an unrealistic path, since for $T \rightarrow \infty$ the parameter $\beta$ will diverge to either $\infty$ or $-\infty$. The hyperbolic path may be more realistic. It expresses fast convergence to a certain fixed value of $\beta$, but with diminishing convergence speed over time. Such a pattern may for example be seen when a government decides to gradually change import levies. Say a company in country $A$ exports products at a cost of $y_{1}$ to country $B$, where due to import levies the product is sold for $y_{2}$. Now the government of country $B$ decides to lower the import levies by 1% per period. We may then find a pattern similar to the pattern in Fig. 1.

For completeness we also consider the case $\omega _{2} < 0$. In that case we get an oscillating pattern for $\beta$ which is difficult to interpret. The result for $\omega = (1.7, -0.89, 0)$ is given below (Fig. 2).

Fig. 2

Simulated beta series from the FVECM–GAS model with beta oscillating around 0.9

Fig. 3

Simulated series from the FVECM–GAS model with ‘quasi-linear’ evolution of beta

The resulting $y_{1}$ and $y_{2}$ series are cointegrated according to the Johansen test, but it is difficult to find a reasonable interpretation for this pattern. Here $\beta$ is hyperbolically decaying but also alternating between positive and negative values. In fact two paths are combined, one where $\beta$ is hyperbolically decaying towards 0.9, and a second path where $\beta$ is hyperbolically increasing towards 0.9. The first path occurs at all odd numbers, the second at all even numbers. Due to the fast convergence, the resulting effect on the $y$ series is not large. The result is similar to the case where $y_{1}$ and $y_{2}$ are simulated from a normal FVECM with $\beta =0.9$.

3.1.2 Stochastic

Of course, the main benefit of the FVECM–GAS model is seen when $\omega _{3} \ne 0$. In that case the vector $\beta$ is influenced by, or in fact interacts with the time series, which allows for much more freedom for the development of $\beta$. First we consider cases with $\omega _{2}$ equal to 1. In Fig. 3 the simulated series for $\omega = (0, 1 , 0.002)$ is shown. It is interesting to see that even if $\omega _{3} \ne 0$, a development of $\beta$ can be seen that is almost linear. One can of course question the benefit of the GAS-component in the model: If the path is quasi-linear, why not use a deterministic model instead? This question can be answered by focusing on the benefits of this stochastic model. A first advantage of this approach is that the decrease is not fixed as in the deterministic case, but is implied by the evolution of the series $y_{1}$ and $y_{2}$. The speed of the decrease can easily change if the data imply this via the update of $\beta$. A second advantage is that the decrease is not explicitly modelled. Without changing $\omega$, the vector $\beta$ can remain constant for some time or can increase again if this is implied by the update $s_{t}$. So we clearly see that the FVECM–GAS model can deal with almost linear paths, but still has some important advantages over a non-stochastic model. By the Johansen test, the resulting variables are cointegrated with rank 1.

We now focus on the flexibility of the model, while still keeping $\omega _{2}$ equal to 1. If we increase $\omega _{3}$ the effect of the update is seen more clearly. In Fig. 4 a simulation is shown for $\omega = (0, 1 , 0.005)$. Even though the parameters in $\omega$ are constant over time, a clear ‘break’ in the path of $\beta$ is seen. The model is thus also very useful to model a sudden change in the cointegration parameter $\beta$. Although a break is seen, the variables in $y$ are still cointegrated according to the Johansen test. This may not be very surprising, since $\omega _{3}$ is still quite small, and since $\omega _{2}$ is equal to 1. The latter implies a very high correlation between the succeeding $\beta$’s.

Fig. 4

Simulated series from the FVECM–GAS model showing a break in the path of beta

Fig. 5

Simulated series from the FVECM–GAS model showing multiple breaks in the path of beta

Fig. 6

Simulated series from the FVECM–GAS model showing a seasonal pattern for beta

Should we however increase $\omega _{3}$ even more, we arrive at a dataset that is not cointegrated according to the Johansen test. An example with $\omega = (0,1,0.03)$ is given in Fig. 5. In this case many jumps in $\beta$ are seen. Due to these jumps, the Johansen test indicates that there is no common trend in these two time series. Now we arrive at a case where we can no longer speak about ‘cointegration’ in the classical meaning of the word, but only about ‘time-varying cointegration’. As one can see, the model can be very useful whenever many structural breaks are present in a market.

If we choose $\omega _{3}$ even larger, we find that $\beta$ diverges to very large values. We therefore now focus on cases with $\omega _{2} \ne 1$. By choosing $\omega = (0.3, 0.7, 0.035)$ we find some sort of alternating pattern as shown in Fig. 6. This can be useful to model seasonal trends. By choosing $\omega _{1}$ larger and $\omega _{2}$ smaller, the period of the seasonal trend becomes shorter. By choosing $\omega _{3}$ larger in absolute sense, the amplitude of the wave increases. In this way the model is capable to deal with various seasonal trends in the $\beta$ parameter. For this example, the series in $y_{1}$ and $y_{2}$ are cointegrated according to the Johansen test, which could be expected by the fact that the $\beta$ is clearly centered around $\pm 0.8$.

3.2 Time-Varying Variance

We now turn to some examples for the case with constant $\beta$, and time-varying (log-)variance $\sigma _{2}$ instead. Note first that the examples below will be inherently different from the ones above, since the model considered here implies a multiplicative trend for the variance, since $e^{\sigma _{t+1}^{2}} = e^{\omega _{1} + \omega _{2} \sigma ^{2}_{t} + \omega _{3} s_{t}} = e^{\omega _{1}} \cdot e^{\omega _{2} \sigma ^{2}_{t}} \cdot e^{\omega _{3} s_{t}}$. The meaning of the vector $\omega$ and its effect on the time-varying parameter will thus be different than in the additive model considered for $\beta$.

3.2.1 Deterministic

Since the model is now multiplicative, a linear trend is no longer possible.³ Should one take $\omega = ( -0.1,1,0)$ the evolution of the log-variance will indeed be linear, but the evolution of the variance will be hyperbolically decaying. If one assumes a hyperbolic path for the log-variance, the path of the variance will be hyperbolic as well, although with different (faster) convergence speed than in the additive model. An example for $\omega = (0, 0.99, 0)$ is given in Fig. 7. One can clearly see that the high variance in the beginning leads to more extreme shocks in the $y$-series, and the reduced variance leads to a calmer trajectory afterwards. This model can be useful if for example increased regulation is encountered in a specific market, leading to less volatile patterns. Also such patterns may be seen in the aftermath of a crisis. Even though $\beta$ is constant in this model, the series $y_{1}$ and $y_{2}$ are not cointegrated according to the Johansen test. Since all other factors have not changed, this will be the result of the time-varying variance.

Of course the deterministic model can be changed by making $\omega _{2}$ larger than 1, in order to model cases where the variance is steadily increasing instead of decreasing.

Fig. 7

Simulated series from the FVECM–GAS model with hyperbolically decaying variance. Note: The second graph shows the variance $e^{\sigma _{t}^{2}}$ for $t=1,\dots ,T$, and not the log-variance. Here, $e^{\sigma _{init}^{2}}=60$

3.2.2 Stochastic

We now turn to the more interesting cases with $\omega _{3} \ne 0$. To illustrate the effect of the changing variance well, we consider the example $\omega = (0.01, 0.99,$-$\,0.0015)$ in Fig. 8.

Fig. 8

Simulated series from the FVECM–GAS model with varying variance. Note: The second graph shows the variance $e^{\sigma _{t}^{2}}$ for $t=1,\dots ,T$, and not the log-variance

In this example one can clearly recognize the sudden increase in the variance around $t = 86$. First of all this illustrates the flexibility of the FVECM–GAS, in that the model allows for structural breaks in the variance. Secondly we note that this behavior is in line with behavior seen in times of crises: a sudden increase in the variance, which then slowly decays towards pre-crisis levels. Thirdly we note that the increased variance affects both time series. Although the cointegration relationship is more difficult to recognize, the relationship still holds. This is also recognized by the Johansen test, it indicates that $y_{1}$ and $y_{2}$ are indeed cointegrated. This however does not mean that estimating an ordinary FVECM would be equally good, since acknowledging that the variance is changing is very important to prevent misspecification.

As is clear from the general outset, many more variance patters can be created with this FVECM–GAS model, and in turn many more time series can be represented by this model. For reasons of conciseness we limit our analysis to this extreme but illustrative case.

3.3 Time-Varying b

In this third part the cointegration degree parameter $b$ is varied. In this case we again have a multiplicative model as in the case with varying variance.⁴

3.3.1 Deterministic

Similar to the previous case, one can create a hyperbolic path for $e^{b}$. A hyperbolic path expresses a cointegration degree that changes at each step, and converges towards a new state. Such a pattern for $e^{b}$ may be appropriate if due to some structural change a convergence towards a (new) cointegration degree is encountered. We will not give an example of such a path here. From this deterministic model one can simulate time series that are cointegrated according to the Johansen test, but also time series that are not. The closer $b$ is to zero, the more likely it is that the Johansen will indicate that the time series are not cointegrated.

3.3.2 Stochastic

Again, let us illustrate the potential of the stochastic model with an example. In Fig. 9 we consider a realization of the case $\omega = (-\,0.001, 1, -\,0.01)$.

Fig. 9

Simulated series from the FVECM–GAS model with downward trend of $e^{b}$. Note: The second graph shows the cointegration degree parameter, i.e. $e^{b}$ for $t=1,\dots ,T$

First the value of $e^{b}$ implies that the variables are strongly cointegrated, but this $e^{b}$ parameter then slowly decays, indicating that the two time series are less cointegrated. Still, according to the Johansen test these time series are cointegrated.

Many reasons can be thought of why a decaying cointegration degree parameter is seen. If we take up the example of a competitive market, Fig. 9 may represent a case where many market actors leave the market. Less economic actors will imply less force to maintain the equilibrium, and larger deviations from the equilibrium are seen. This is reflected by a lower cointegration degree $e^{b}$.

Let us finally focus on a model where $b$ become so small that the Johansen test cannot reject the hypothesis of no cointegration. An example with $\omega = (0, 1, 0.3)$ is given in Fig. 10.

Fig. 10

Simulated series from the FVECM–GAS model with small values of $e^{b}$. Note: The second graph shows the cointegration degree parameter, i.e. $e^{b}$ for $t=1,\dots ,T$. Here, $e^{b_{init}} = e^{-4} \approx 0.018$

The cointegration degree is very small in this case and the Johansen test indicates absence of a cointegration relationship between $y_{1}$ and $y_{2}$. Still, one can see that the variables tend to commove. This is an example of how the FVECM–GAS model can add to ordinary FVECM models. This example also illustrates that the FVECM–GAS model can handle time series that are not cointegrated for some time, but whose $b$ increases afterwards. This is especially important if time series over a long horizon are considered. Due to some disturbance it may well be that the cointegration relationship is temporarily not present, but is seen again afterwards. Should one conclude that the variables are not cointegrated at all, misspecification may lead to erroneous results.

4 Estimation

Now that some simulated series from the FVECM–GAS model have been shown, we consider estimation of the parameters in the FVECM–GAS model. In the previous Section we have considered all three models, now for conciseness we only consider the model with time-varying $\beta$. However, similar results for the two other models were found.

First we estimate the correct FVECM–GAS models for some simulated series shown in the previous Section. Secondly, we consider how severe misspecification is by estimating a FVECM model (i.e. with fixed $\beta$) on the simulated series for which the true DGP has a time-varying $\beta$.

4.1 Estimation of Correct Model

It is important to check whether the FVECM–GAS with time-varying $\beta$ can be estimated well. In Table 1 an example with $N=1000$ is shown to illustrate that estimation is very well possible.

Table 1 Simulation parameters and parameter estimates for the FVECM–GAS with time-varying beta

We see that the parameters are very well estimated, and that all 95% confidence intervals contain the true parameters. This is easily seen by noticing that all the true parameters are less that 1.96 standard deviations away from the parameter estimates. Also if other parameter values are chosen for the DGP, estimation shows that no problems are encountered when estimating the FVECM–GAS model.

Once a FVECM–GAS model has been estimated, one can easily perform some specification tests. First one can test whether $\beta$ in the model is deterministic ($H_{0}$) or stochastic ($H_{1}$):

$$\begin{aligned} H_{0}: \; \; \omega _{3} = 0,\\ H_{1}: \; \; \omega _{3} \ne 0. \end{aligned}$$

This can be performed with the well-known $t$-test. In specific cases one may also decide to perform a one-sided test on $\omega _{3}$, although the interpretation depends on the specific model at hand.

Another possibility is to test whether $\beta$ is constant and deterministic ($H_{0}$) or time-varying ($H_{1}$) using the following test:

$$\begin{aligned}&H_{0}: \; \; \frac{\omega _{1}}{\beta _{init}} + \omega _{2} = 1 \; \; \wedge \; \; \omega _{3} = 0,\\&H_{1}: \; \; \text {not} \; \; H_{0} \end{aligned}$$

This test follows directly from the observation that $\beta$ is time-invariant and deterministic if and only if $\omega _{1} + \omega _{2} \cdot \beta _{init} = \beta _{init}$, and can be performed with an $F$-test both if $\beta _{init}$ is initialized deterministically or stochastically. One can extend the analysis and perform more tests with other restrictions depending on the problem at hand.

4.2 Estimation of Incorrect Model

Table 2 Parameters used for simulating from the (stochastic) FVECM–GAS with hyperbolically decaying beta and resulting from estimation of the FVECM model

In Table 2 we consider the case that the series $\beta$ converges towards 0.909 (see Fig. 1) and one can see that a 95% confidence interval of $\hat{\beta }$ contains this value. The $\alpha$-parameters are not estimated correctly, and also the $b$ and $d$ parameters are not contained in the 95% confidence bounds. So we clearly see that in this case estimating a FVECM instead of a FVECM–GAS yields very bad results.

Table 3 Parameters used for simulating from the (stochastic) FVECM–GAS with decaying beta and resulting from estimation of the FVECM model

Table 3 represents the stochastic case for which the series $\beta$ slowly moves downwards (see Fig. 3). The estimate $\hat{\beta }$ is a sort of average of the series $\beta$. Although this implies a loss of information, the other parameters are quite well estimated. Only small problems are encountered with the estimate of $d$. The parameter $b$, although with a large standard error, is underestimated. This may be due to the simplification in $\beta$, implying that the correct linear combination is estimated to be $I(0.35)$ instead of $I(0.2)$ because of more presumed deviations from the equilibrium.

Table 4 Parameters used for simulating from the (stochastic) FVECM–GAS with decaying beta and resulting from estimation of the FVECM model

We consider one final case to visualize what happens when estimating a FVECM model instead of a FVECM–GAS model. As we can see from Table 4 and Fig. 11 the FVECM model takes as estimate for the $\beta$ series some kind of average. Of course, this is a large simplification of the true model. Especially if we compare these results with the very good estimation results of the FVECM–GAS in Table 1, we can clearly see that neglecting the time-variance of $\beta$ leads to severe and unnecessary estimation problems.

Fig. 11

Evolution of beta in the FVECM–GAS model compared with its fixed FVECM estimate

5 Real-World Data

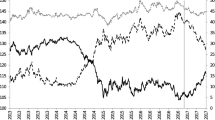
In this Section we illustrate the differences between the FVECM and the new FVECM–GAS model by estimation on a real-world dataset. The data is taken from the Climate Research Unit (CRU), one of the world’s leading institutions concerned with the study of natural and anthropogenic climate change. In this case we consider a CRU dataset⁵ with temperature anomalies for both the northern and southern hemisphere (‘NH’ and ‘SH’, respectively), as can be seen in the first graph in Fig. 12. The data range from 1850 until 2016, and are cointegrated according to the Johansen test. More about calculation of these anomalies can be found on the CRU website.

From Fig. 12 it is clear that the time series are non-stationary, and an upward trend is seen. This might reflect the presumed ‘global warming’ theories. A second important notion is that the ratio between the two temperature series is not constant, which can be seen more clearly in the second pane of Fig. 12. Intuitively, one can understand that many common factors such as the sunbeams will affect both time series, but also some idiosyncratic effects will be important. Since these two types of effects may not be always balanced, it is likely that the cointegration relationship between the anomalies for the northern and southern hemisphere will be time-varying.

Fig. 12

Temperature anomalies for the northern (NH) and southern (SH) hemisphere from 1850 until 2016, the ratio between the time series and estimation results for beta

In order to compare the different models well, Table 5 shows the results for the FVECM and the FVECM–GAS with time-varying $\beta$. This latter model is chosen since it not only provides the best results, but also complies with intuition best.

Table 5 Parameter estimates of the FVECM and FVECM–GAS model with time-varying beta, based on temperature anomaly series for the northern and southern hemisphere

It is immediately clear from the Table 5 that the FVECM model very much simplifies the path of $\beta$ that is proposed by the FVECM–GAS model. These paths are depicted in the third pane of Fig. 12. The FVECM–GAS path complies with the observation that the two time series are following a very similar path in the first part of the dataset, but show more variation and ‘divergence’ afterwards. Especially from 1990 onwards, the temperature anomaly in the northern hemisphere increases much faster than in the southern hemisphere. This is very well reflected with a steady increase in $\beta$ from 1990 until the end of the dataset in 2016. The FVECM model fails to reflect this trend. Also we note that the FVECM–GAS model is not just a reflection of the ratio between the two time-series, shown in the second pane of Fig. 12. If one of the time series is very close to 0, the ratio will be very large (in absolute sense) as can be seen around 1952 and 1970. The FVECM–GAS model easily deals with these situations where one of the time series is almost 0.

An immediate consequence of the failure to reflect the trend in $\beta$, is that the FVECM model severely understates the cointegration degree $b$. In the FVECM model $b$ is estimated close to 0, which leads to very large values for $\alpha _{1}$ and $\alpha _{2}$. The cointegration degree $b$ is much larger in the FVECM–GAS model. Here we can clearly see that if one does not account for time-variance in $\beta$, the cointegration relationship may be almost hidden.

The difference is also reflected in the values of the average log-likelihood, 1.395 and 1.351 for the FVECM–GAS and the regular FVECM respectively. The latter model fits the data worse, due to a simplification of the $\beta$ pattern and thus an understatement of the cointegration degree.

6 Conclusions

In this paper three FVECM models with time-varying parameters were introduced and compared with their fixed parameter counterparts, because of presumed shortcomings of the latter models. In order to ensure that no predetermined path for the time-varying parameters was set, the GAS framework was used for all three models. It was shown that this GAS framework allows for many different patterns: linear, hyperbolic, quasi-linear patterns, but also more flexible ones and even a pattern with a seasonal trend. All these models may be very useful and have easy, real-world interpretations and thus extend the FVECM model in a useful manner.

With simulated as well as with real-world data, the FVECM–GAS models performs well. These three models also show the weaknesses of the more common FVECM model. It may be incorrectly specified in the first place, but also we have seen examples of how variables are ‘time-varying cointegrated’, whereas this is not recognized by the Johansen test. Should one as a result choose to abandon the FVECM models, a second source of errors has arisen. In further research one can try to design a test for time-varying cointegration, in order to prevent misspecification.

Three options were given on how to adapt the FVECM model. More extensions could be thought of, for example a model with multiple time-varying parameters could be considered by choosing e.g. $f_{t} = (\beta _{t},\sigma _{t}^{2})$ or any other multidimensional parameter set. An intuitive explanation for this specific example may be that if some structural changes imply a changing $\beta$, this may be accompanied by a temporary large uncertainty, i.e. a larger variance. In the same fashion many more interpretations can be given, that of course need underpinning by economic theory. Of course also models with different error distributions could be considered.

It is important to recognize that time-varying cointegration need not be absent if the FVECM model indicates that $\beta$ is not significantly different from 0. Suppose $\beta$ evolves linearly from 1 to $-1$, the FVECM model may indicate that $\beta$ is zero, but using a FVECM–GAS approach the underlying pattern of $\beta$ may be found. We therefore hope that more extensions of the FVECM model will be made by making parameters time-varying, in order to fully make use of the (time-varying) cointegration relationships present in many real-world datasets.

Appendix

In simulating the data for Sect. 3, 220 data points were simulated of which the first 20 were used as a ‘burn-in period’. The simulation has been performed in the program ‘Ox’, see Doornik (2007), with random seed 7, i.e. with using the function ‘ranseed(7)’. The other parameters are stated below in Table 6.

Table 6 Parameters used for simulating the three FVECM–GAS models in Sect. 3

When a certain parameter is made time-varying, then the same value is used as starting value. So in the FVECM–GAS with varying $\beta$, we take $\beta _{init} = 1.000$. If a different starting value is chosen, this is stated in Sect. 3.