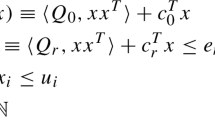Abstract
The Constraint Satisfaction Problem (CSP) framework allows users to define problems in a declarative way, quite independently from the solving process. However, when the problem is over-constrained, the answer “no solution” is generally unsatisfactory. A Max-CSP \(\mathcal{P}_m = \langle V, \textbf{D}, C \rangle\) is a triple defining a constraint problem whose solutions maximize the number of satisfied constraints. In this paper, we focus on numerical CSPs, which are defined on real variables represented as floating point intervals and which constraints are numerical relations defined in intension. Solving such a problem (i.e., exactly characterizing its solution set) is generally undecidable and thus consists in providing approximations. We propose a Branch and Bound algorithm that provides under and over approximations of a solution set that maximize the maximum number \({m_{\mathcal P}}\) of satisfied constraints. The technique is applied on three numeric applications and provides promising results.
Similar content being viewed by others
References
Benhamou, F., Goualard, F., Granvilliers, L., & Puget, J.-F. (1999). Revising hull and box consistency. In Proceedings of the 1999 international conference on logic programming, ICLP’99 (pp. 230–244). Cambridge, MA, USA: Massachusetts Institute of Technology.
Benhamou, F., Goualard, F., Languenou, E., & Christie, M. (2004). Interval constraint solving for camera control and motion planning. ACM Transactions on Computational Logic, 5(4), 732–767.
Benhamou, F., McAllester, D., & van Hentenryck, P. (1994). CLP(intervals) revisited. In International logic programming symposium, ILPS ’94 (pp. 124–138). Cambridge: MIT.
Benhamou, F., & Older, W. J. (1997). Applying interval arithmetic to real, integer and Boolean constraints. Journal of Logic Programming, 32(1), 1–24.
Borning, A., Freeman-Benson, B., & Wilson, M. (1992). Constraint hierarchies. Lisp and Symbolic Computation, 5(3), 223–270.
Byrd, R. H., Nocedal, J., & Waltz, R. A. (2006). KNITRO: An integrated package for nonlinear optimization. In Large-scale nonlinear optimization (pp. 35–59). New York: Springer.
Christie, M., & Normand, J.-M. (2005). A semantic space partitionning approach to virtual camera control. In Proceedings of the annual eurographics conference (Vol. 24, pp. 247–256).
Christie, M., Normand, J.-M., & Truchet, C. (2006). Computing inner approximations of numerical MaxCSP. In Interval analysis, constraint propagation, applications, IntCP 2006.
Collavizza, H., Delobel, F., & Rueher, M. (1999). Extending consistent domains of numeric CSP. In IJCAI ’99: Proceedings of the sixteenth international joint conference on artificial intelligence (pp. 406–413).
de Givry, S., Larrosa, J., Meseguer, P., & Schiex, T. (2003). Solving Max-SAT as weighted CSP. In Principles and practice of constraint programming, CP 2003 (pp. 363–376). New York: Springer.
Delanoue, N., Jaulin, L., & Cottenceau, B. (2004). Counting the number of connected components of a set and its application to robotics. In PARA (pp. 93–101).
Dongarra, J. (2007). Performance of various computers using standard linear equations software. Technical report CS-89-85, University of Tennessee.
Drezner, Z., & Hamacher, H. W. (Eds.) (2002). Facility location. Applications and theory. New York: Springer.
Goldberg, D. (1991). What every computer scientist should know about floating-point arithmetic. Computing Surveys, 23(1), 5–48.
Hayes, B. (2003). A lucid interval. American Scientist, 91(6), 484–488.
Hirsch, M. J., Meneses, C. N., Pardalos, P. M., & Resende, M. G. C. (2007). Global optimization by continuous grasp. Optimization Letters, 1, 201–212.
Jaulin, L., & Walter, E. (1993). Guaranteed nonlinear parameter estimation from bounded-error data via interval analysis. Mathematics and Computers in Simulation, 35(2), 123–137.
Jaulin, L., & Walter, E. (2002). Guaranteed robust nonlinear minimax estimation. IEEE Transaction on Automatic Control, 47(11), 1857–1864.
Jaulin, L., Walter, E., & Didrit, O. (1996). Guaranteed robust nonlinear parameter bounding. In CESA’96, IMACS multiconference (symposium on modelling, analysis and simulation) (pp. 1156–1161).
Lhomme, O. (1993). Consistency techniques for numeric CSPs. In IJCAI ’93: Proceedings of the thirteenth international joint conference on artificial intelligence (pp. 232–238).
Mackworth, A. K. (1977). Consistency in networks of relations. Artificial Intelligence, 8(1), 99–118.
Milanese, M., & Vicino, A. (1991). Estimation theory for nonlinear models and set membership uncertainty. Automatica, 27(2), 403–408.
Minton, S., Johnston, M. D., Philips, A. B., & Laird, P. (1992). Minimizing conflicts: A heuristic repair method for constraint satisfaction and scheduling problems. Artificial Intelligence, 58(1–3), 161–205.
Moore, R. E. (1966). Interval analysis. Englewood Cliffs: Prentice-Hall.
Murtagh, B. A., & Saunders, M. A. (1998). Minos 5.5 user’s guide. Technical report, Systems Optimization Laboratory, Department of Operations Research, Stanford University.
Neumaier, A. (1990). Interval methods for systems of equations. Cambridge: Cambridge University Press.
Normand, J.-M. (2008). Placement de caméra en environnements virtuels. PhD thesis, Université de Nantes.
Petit, T., Régin, J.-C., & Bessière, C. (2002). Range-based algorithm for Max-CSP. In Principles and practice of constraint programming, CP 2002 (pp. 280–294). New York: Springer.
Wallace, R. J. (1996). Analysis of heuristic methods for partial constraint satisfaction problems. In Principles and practice of constraint programming, CP 1996 (pp. 482–496). New York: Springer.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Normand, JM., Goldsztejn, A., Christie, M. et al. A branch and bound algorithm for numerical Max-CSP. Constraints 15, 213–237 (2010). https://doi.org/10.1007/s10601-009-9084-1
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10601-009-9084-1