Skip to main content
SpringerLink
Log in

Numerical Assessment of the Informational Influence of Election Campaigns on the Electorate

  • Published:
Computational Mathematics and Modeling Aims and scope Submit manuscript

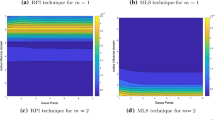
A numerical scheme is developed for the assessment of the informational influence of election campaigns on the electorate. It relies on the determination of the probability density function of stochastic dynamic system states that requires a numerical solution of the Fokker–Planck–Kolmogorov equation reduced to a system of ordinary differential equations in the projection form of the Galerkin method. The approximation of the probability density function in state variables is specified on a triangulation in the system of Gaussian basis functions assuming time-dependent expansion coefficients. Convergence of the proposed numerical scheme is examined in the context of the convergence of the mean-square approximation of a function on a simplex. Some features of the algorithmic implementation of the solution are considered and comparative modeling results are reported for test problems.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. I. S. Polyanskii, K. O. Loginov, N. I. Il’in, and A. S. Velikikh, “Mathematical model of assessing the informational influence of election campaigns in social media on the electorate,” Matem. Modelirovanie, 34, No. 1 (2022).

  2. A. P. Petrov, A. I. Maslov, and N. A. Tsaplin, “Modeling the choice of positions by individuals in an informational confrontation in a society,” Matem. Modelirovanie, 27, No. 12, 137–148 (2015).

    MATH  Google Scholar 

  3. A. P. Mikhailov, A. P. Petrov, G. B. Pronchev, and O. G. Proncheva, “Modeling the decline of social attention to a one-time past political event,” Doklady AN, 480, No. 4, 397–400 (2018); DOI: https://doi.org/10.7868/S0869565218160028.

    Article  Google Scholar 

  4. A. P. Petrov and O. G. Proncheva, “Modeling the choice of positions by individuals in an informational confrontation with a two-item agenda,” Matem. Modelirovanie, 31, No. 7, 91–108 (2019).

    Article  Google Scholar 

  5. A. P. Mikhailov, A. P. Petrov, and O. G. Proncheva, “A model of the propagation of information in a society,” Matem. Modelirovanie, 26, No. 3, 65–74 (2014).

    Google Scholar 

  6. A. S. Il’inskii, I. S. Polyanskii, and D. E. Stepanov, “Convergence of the barycentric method for inner Dirichlet and Neumann problems in ℝ2 for the Helmholtz equation,” Vestnik Udmurt. Univ., Math., Mechan., Computer Sci., 31, No. 1, 3–18 (2021).

  7. I. S. Polyanskii, “Barycentric method in optimal control of the reflector surface shapre in a mirror antenna,” Matem. Modelirovanie, 29, No. 11, 140–150 (2017).

    Google Scholar 

  8. P. C. Kainen, V. Kurkova, and M. Sanguineti, “Estimates of approximation rates by Gaussian radial-basis functions,” CANNGA 2007, Adaptive and Natural Computing Algorithms, pp. 11–18; DOI: 10.1007/978-3-540-71629-7 2.

  9. I. K. Daugavet, Theory of Approximate Methods. Linear Equations, 2nd edition, BKhV-Peterburg, St. Peterburg (2006).

  10. N. N. Kalitkin, Numerical Methods [in Russian], Nauka, Moscow (1978).

    Google Scholar 

  11. I. S. Gradshtein and I. M. Ryzhik, Tables of Integrals, Sums, Series, and Products [in Russian], 4th edition, Fizmatlit, Moscow (1963).

    Google Scholar 

  12. G. E. Andrew and B. C. Berndt, Ramanujan’s Lost Notebook, Part V, Springer, New York (2013).

  13. R. Strichartz, A Guide to Distribution Theory and Fourier Transforms, World Scientific (2003).

    Book  Google Scholar 

  14. V. A. Emelichev, M. M. Kovalev, and M. K. Kravtsov, Polyhdera, Graphs, Optimization (Combinatoril Theory of Polyhedra) [in Russian], Nauka, Moscow (1981).

    Google Scholar 

  15. I. S. Polyanskii, D. E. Stepaov, D. K. Ketukh, and V. A. Shevchenko, “Electrodynamic analysis of mirror antennas in the barycentric approximation,” Fizika Volnovykh Protsessove i Radiotekhnicheskie Sistemy, 23, No. 4, 36–47 (2020).

    Google Scholar 

  16. T. H. Cormen, C. E. Leiserson, R. L. Rivest, and C. Stein, Introduction to Algorithms: Design and Analysis [Russian translation], Vilyams Publ. House, Moscow (2010).

    MATH  Google Scholar 

  17. I. S. Polyanskii, N. S. Arkhipov, and S. Yu. Misyuri, “Solution of the optimal control problem for an adaptive multibeam mirror antenat,” Avtomat. Telemekh., No. 1, 83–100 (2019).

    Google Scholar 

  18. J. R. Dormand and P. J. Prince, “A family of embedded Runbe–Kutta formulae,” J. Comp. Appl. Math., 6, No. 1, 19–16 (1980); DOI: https://doi.org/10.1016/0771-050X(80)90013-3.

Download references

Author information

Authors and Affiliations

  1. Faculty of Computational Mathematics and Cybernetics, Lomonosov Moscow State University, Moscow, Russia

    A. S. Il’inskii

  2. Academy of Russian Federal Defense Forces, Moscow, Russia

    I. S. Polyanskii

  3. Administration for Information and Telecommunication Support, Service for Special Communication and Information, Russian Federal Defense Forces, Moscow, Russia

    K. O. Loginov

  4. “Evrika” Stock Company, St. Petersburg, Russia

    N. S. Arkhipov

Authors
  1. A. S. Il’inskii
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. I. S. Polyanskii
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. K. O. Loginov
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. N. S. Arkhipov
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to A. S. Il’inskii.

Additional information

Translated from Problemy Dinamicheskogo Upravleniya, Issue 68, 2021, pp. 15–28.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Il’inskii, A.S., Polyanskii, I.S., Loginov, K.O. et al. Numerical Assessment of the Informational Influence of Election Campaigns on the Electorate. Comput Math Model 32, 399–412 (2021). https://doi.org/10.1007/s10598-022-09542-5

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10598-022-09542-5

Keywords

Search

Navigation