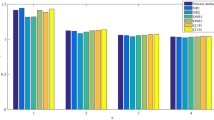
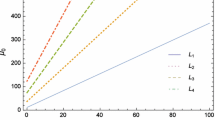
In this article, a modification of Newton’s method with fifteenth-order convergence is presented. The modification of Newton’s method is based on the method of fifth-order convergence of Hu et al. First, we present theoretical preliminaries of the method. Second, we solve some nonlinear equations and then systems of nonlinear equations obtained by means of the finite element method. In contrast to the eleventh-order M. Raza method, the fifteenth-order method needs less function of evaluation per iteration, but the order of convergence increases by four units. Numerical examples are given to show the efficiency of the proposed method.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
S. N. Atluri, Methods of Computer Modeling in Engineering and Sciences, Tec. Sci. Press (2002).
S. N. Atluri, H. T. Liu, and Z. D. Han, “Meshless local Petrov–Galerkin (MLPG) mixed collocation method for elasticity problems,” Comput. Model. Eng. Sci., 14, 141–152 (2006).
S. N. Atluri and S. Shen, “The meshless local Petrov–Galerkin (MLPG) method: a simple and less-costly alternative to the finite and boundary element methods,” Comput. Model. Eng. Sci., 3, 11–51 (2002).
M. Kumar, A. K. Singh, and A. Srivastava, “Various Newton-type iterative methods for solving nonlinear equations,” J. Egypt. Math. Soc., 21, 334–339 (2013).
X. Li, Z. Wu, L. Wang, and Q. Zhang, “A ninth-order Newton-type method to solve systems of nonlinear equations,” J. Res. Rev. App. Sci., 16, 224–228 (2013).
M. Raza, “Eleventh-order convergent iterative method for solving nonlinear equations,” Int. J. Appl. Math., 25, 365–371 (2012).
Z. Hu, L. Guocai, and L. Tian, “An iterative method with ninth-order convergence for solving nonlinear equations,” Int J. Contemp. Math. Sci., 6, 17–23 (2011)
M. A. Noor, W. A. Khan, K. I. Noor, and E. Al-Said, “Higher-order iterative methods free from second derivative for solving nonlinear equations,” Int. J. Phys. Sci., 6, 1887–1893 (2011).
I. A. Al-Subaihi, M. T. Shatnawi, and H. I. Siyyam, “A ninth-order iterative method free from second derivative for solving nonlinear equations,” Int. J. Math. Anal., 5, 2337–2347 (2011).
J. Alberty, C. Carstensen, and S. A. Funken, “Remarks around 50 lines of Matlab: short finite element implementation,” Numer. Algorithms, 20, 117–137 (1999).
M. Kumar, A. Srivastava, and A. K. Singh, “Numerical simulation of singularly perturbed nonlinear elliptic boundary value problems using finite element method,” Appl. Math. Comput., 219, 226–236 (2012).
M. Kumar and P. Kumar, “A finite element approach for finding positive solutions of semilinear elliptic Dirichlet problems’,” Numer. Methods Part. Differ. Equ., 25, 1119–1128 (2009).
M. Kumar and P. Kumar, “Computational method for finding various solutions for a quasilinear elliptic equation of Kirchhoff type,” Adv. Eng. Softw., 40, 1104–1111 (2009).
J. F. Traub, Iterative Methods for the Solution of Equations, Prentice-Hall, Englewood Cliffs, New Jersey (1964).
J. Kou, Y. Li, and X. Wang, “Some variants of Ostrowski’s method with seventh-order convergence,” J. Comput. Appl. Math., 209, 153–159 (2007).
M. T. Darvishi and A. Barati, “Super cubic iterative methods to solve systems of nonlinear equations,” Appl. Math. Comput., 188, 1678–1685 (2007).
W. Bi, H. Ren, and Q. Wu, “New family of seventh-order methods for nonlinear equations,” Appl. Math. Comput., 203, 408–412 (2008).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Srivastava, A. An Iterative Method with Fifteenth-Order Convergence to Solve Systems of Nonlinear Equations. Comput Math Model 27, 497–510 (2016). https://doi.org/10.1007/s10598-016-9339-9
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10598-016-9339-9