Skip to main content
SpringerLink
Log in

Numerical method for soliton solutions

  • Published:
Computational Mathematics and Modeling Aims and scope Submit manuscript

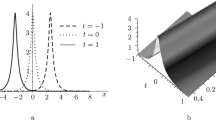
An iterative method is proposed for finding soliton solutions of the Korteweg–de Vries equation. The method also finds soliton solutions of other nonlinear evolution differential equations. The method is virtually independent of the specific nonlinearity of the operator. A feature of the method is the weak dependence of convergence on the form of the initial function.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. R. M. Miura, C. S. Gardner, and M. D. Kruscal, “Korteweg–de Vries equation and generalizations. II. Existence of conservation laws and constants of motion,” J. Math. Phys., 9, 1204–1209 (1968).

    Article  MATH  Google Scholar 

  2. T. V. Dorokhova, N. P. Savenkova, and V. A. Trofimov, “Simulation of soliton solutions in the problem of propagation of a femtosecond pulse in a medium with cubic nonlinearity,” Prikl. Matem. Informat., No. 2, 63–68, MGU (1999).

  3. N. K. Sheklovnikov, “Solitons in fluids,” Nonlinear Processes in Dynamical Systems [in Russian], 3(2), 17–26 (2009).

    Google Scholar 

  4. T. Miwa, M. Jimbo, and E. Date, Solitons: Differential Equations, Symmetries and Infinite Dimensional Algebras, Cambridge University Press (2000) [Russian translation MTsNIO, Moscow (2005)].

Download references

Author information

Authors and Affiliations

  1. Faculty of Computational Mathematics and Cybernetics, Moscow State University, Moscow, Russia

    V. S. Laponin, N. P. Savenkova & V. P. Il’yutko

Authors
  1. V. S. Laponin
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. N. P. Savenkova
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. V. P. Il’yutko
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to V. S. Laponin.

Additional information

Translated from Prikladnaya Matematika i Informatika, No. 38, pp. 18–30, 2011.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Laponin, V.S., Savenkova, N.P. & Il’yutko, V.P. Numerical method for soliton solutions. Comput Math Model 23, 254–265 (2012). https://doi.org/10.1007/s10598-012-9135-0

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10598-012-9135-0

Keywords

Search

Navigation