Skip to main content
SpringerLink
Log in

A generalized time-domain velocity-stress seismic wave equation for composite viscoelastic media with a topographic relief and an irregular seabed

  • Original Paper
  • Published:
Computational Geosciences Aims and scope Submit manuscript

Abstract

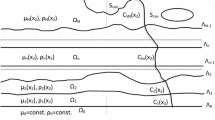
Accurate seismic wave modeling of viscoelastic anisotropic medium is a fundamental tool for seismic data processing, interpretation and full waveform inversion. Also, free water surface, topographic relief and irregular seabed are often encountered in practical seismic surveys. Thus, basing on the General Maxwell Body, we proposed a generalized matrix form of the velocity-stress seismic wave equation, which becomes valid for composite viscoelastic anisotropic media and satisfies the boundary conditions in presence of topographic free surfaces and irregular fluid–solid interfaces. We theoretically show that the viscoelastic effect of a medium may be considered as the intrinsic body sources accumulated in wavefield history and computed by a recursive convolution formula accurately and efficiently. We also demonstrated that such a generalized viscoelastic wave equation may be solved with the curvilinear MacCormack finite difference method and validated the accuracy and feasibility of the proposed method. The modeling results in homogeneous and heterogeneous media match well with the analytical solutions and the references yielded by the spectral element solutions.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Data availability

Data sharing not applicable to this article as no datasets were generated during the current study.

Code availability

The analytical solution code is download from Seismic wave Propagation and Imaging in Complex media: a European network (SPICE) website (EX2DDIR/ EX2DELEL package, http://www.spice-rtn.org/library/software.1.html) The spectral element code is downloaded from the Computational Infrastructure for Geodynamics (CIG) website (SPECFEM2D package, https://geodynamics.org/cig/software/ specfem2d/).

References

  1. Aki, K., Richards, P. G.: Quantitative seismology: Theory and methods, San Francisco, California (1980)

  2. Appelö, D., Petersson, N.A.: A stable finite difference method for the elastic wave equations on complex geometries with free surfaces. Comm. Comput. Phys. 5, 84–107 (2009)

    Google Scholar 

  3. Bai, T., Tsvankin, I.: Time-domain finite-difference modeling for attenuative anisotropic media. Geophysics 81, C69–C77 (2016). https://doi.org/10.1190/geo2015-0424.1

    Article  Google Scholar 

  4. Blanch, J.O., Robertsson, J.O., Symes, W.W.: Modeling of a constant Q; methodology and algorithm for an efficient and optimally inexpensive viscoelastic technique. Geophysics 60, 176–184 (1995). https://doi.org/10.1190/1.1443744

    Article  Google Scholar 

  5. Cao, D., Yin, X.: Equivalence relations of generalized rheological models for viscoelastic seismic-wave modeling. Bull. Seismol. Soc. Am. 104(1), 260–268 (2014). https://doi.org/10.1785/0120130158

    Article  Google Scholar 

  6. Cao, J., Chen, J.B.: A parameter-modified method for implementing surface topography in elastic-wave finite-difference modeling. Geophysics 83, T313–T332 (2018). https://doi.org/10.1190/geo2018-0098.1

    Article  Google Scholar 

  7. Carcione, J. M.: Wave fields in real media: Theory and numerical simulation of wave propagation in anisotropic, anelastic, porous and electromagnetic media. Elsevier, New York (2007)

  8. Chaljub, E., Komatitsch, D., Vilotte, J.P., Capdeville, Y., Valette, B., Festa, G.: Spectral-element analysis in seismology. Adv. Geophys. 48, 365–419 (2007). https://doi.org/10.1016/S0065-2697(06)48007-9

    Article  Google Scholar 

  9. Chen, J.B., Cao, J., Li, Z.: A comparative study on the stress image and adaptive parameter-modified methods for implementing free surface boundary conditions in elastic wave numerical modeling. Geophysics 86, T451–T467 (2021). https://doi.org/10.1190/geo2020-0418.1

    Article  Google Scholar 

  10. de Hoop, A.T.: Pulsed electromagnetic radiation from a line source in a two-media configuration. Radio Sci. 14, 253–268 (1979). https://doi.org/10.1029/RS014i002p00253

    Article  Google Scholar 

  11. de la Puente, J., Ferrer, M., Hanzich, M., Castillo, J.E., Cela, J.M.: Mimetic seismic wave modeling including topography on deformed staggered grids. Geophysics 79(2), T125–T141 (2014). https://doi.org/10.1190/geo2013-0371.1

    Article  Google Scholar 

  12. Dong, S.L., Chen, J.B., Li, Z.: Viscoelastic wave finite-difference modeling in the presence of topography with adaptive free-surface boundary condition. Acta Geophys. 69, 2205–2217 (2021). https://doi.org/10.1007/s11600-021-00666-7

    Article  Google Scholar 

  13. Dong, S.L., Zhou, X.H., Chen, J.B.: Finite-difference modeling with topography using 3D viscoelastic parameter-modified free-surface condition. Geophysics 88, T211–T226 (2023). https://doi.org/10.1190/geo2022-0556.1

    Article  Google Scholar 

  14. Emmerich, H., Korn, M.: Incorporation of attenuation into time-domain computations of seismic wave fields. Geophysics 52, 1252–1264 (1987). https://doi.org/10.1190/1.1442386

    Article  Google Scholar 

  15. Fornberg, B.: The pseudospectral method: Accurate representation of interfaces in elastic wave calculations. Geophysics 53, 625–637 (1988). https://doi.org/10.1190/1.1442497

    Article  Google Scholar 

  16. Graves, R.W.: Simulating seismic wave propagation in 3D elastic media using staggered-grid finite differences. Bull. Seismol. Soc. Am. 86, 1091–1106 (1996)

    Article  Google Scholar 

  17. Hixon, R., Turkel, E.: Compact implicit MacCormack-type schemes with high accuracy. J. Comput. Phys. 158, 51–70 (2000). https://doi.org/10.1006/jcph.1999.6406

    Article  Google Scholar 

  18. Igel, H., Mora, P., Riollet, B.: Anisotropic wave propagation through finite-difference grids. Geophysics 60, 1203–1216 (1995). https://doi.org/10.1190/1.1443849

    Article  Google Scholar 

  19. Jin, C., Zhou B., Greenhalgh, S., Won, M., Riahi, M.K., Zemerly, M. J.: Generalized recursive convolution method for viscoelastic wave modelling. 84th EAGE Annual Conference & Exhibition, (2023). https://doi.org/10.3997/2214-4609.202310142

  20. Kelley, D. F., Luebbers, R. J.: Piecewise linear recursive convolution for dispersive media using FDTD. IEEE Trans. Antennas Propag. 44, 792–797 (1996). https://doi.org/10.1109/8.509882

  21. Konuk, T., Shragge, J.: Tensorial elastodynamics for anisotropic media. Geophysics 86(4), T293–T303 (2021). https://doi.org/10.1190/geo2020-0156.1

    Article  Google Scholar 

  22. Kristek, J., Moczo, P., Galis, M.: Stable discontinuous staggered grid in the finite-difference modelling of seismic motion. Geophys. J. Int. 183, 1401–1407 (2010). https://doi.org/10.1111/j.1365-246X.2010.04775.x

    Article  Google Scholar 

  23. Kristek, J., Moczo, P.: Seismic-wave propagation in viscoelastic media with material discontinuities: A 3D fourth-order staggered-grid finite-difference modeling. Bull. Seismol. Soc. Am. 93, 2273–2280 (2003). https://doi.org/10.1785/0120030023

    Article  Google Scholar 

  24. Lan, H., Zhang, Z.: Three-dimensional wave-field simulation in heterogeneous transversely isotropic medium with irregular free surface. Bull. Seismol. Soc. Am. 101, 1354–1370 (2011). https://doi.org/10.1785/0120100194

    Article  Google Scholar 

  25. Liu, X., Chen, J., Zhao, Z., Lan, H., Liu, F.: Simulating seismic wave propagation in viscoelastic media with an irregular free surface. Pure Appl. Geophys. 175, 3419–3439 (2018). https://doi.org/10.1007/s00024-018-1879-9

    Article  Google Scholar 

  26. Liu, X.: Modeling seismic waves in ocean with the presence of irregular seabed and rough sea surface. J. Geophys. Eng. 20, 49–66 (2023). https://doi.org/10.1093/jge/gxac093

    Article  Google Scholar 

  27. Luebbers, R., Hunsberger, F.P., Kunz, K.S., Standler, R.B., Schneider, M.: A frequency-dependent finite-difference time-domain formulation for dispersive materials. IEEE Trans. Electromagn. Compat. 32, 222–227 (1990). https://doi.org/10.1109/15.57116

    Article  Google Scholar 

  28. MacCormack, R.W.: The effect of viscosity in hypervelocity impact cratering. Frontiers of Computational Fluid Dynamics. 27–43 (2002).  https://doi.org/10.1142/9789812810793_0002

  29. Mavko, G., Mukerji, T., Dvorkin, J.: The rock physics handbook. Cambridge University Press. (2020). https://doi.org/10.1017/9781108333016

  30. Moczo, P., Kristek, J., Galis, M., Pazak, P., Balazovjech, M.: The finite-difference and finite-element modeling of seismic wave propagation and earthquake motion. Acta Phys. Slovaca 57 (2007). https://doi.org/10.2478/v10155-010-0084-x

  31. Moczo, P., Kristek, J., Galis, M.: The finite-difference modelling of earthquake motions: Waves and ruptures. Cambridge University Press. (2014). https://doi.org/10.1017/CBO9781139236911

  32. Moczo, P., Kristek, J., Halada, L.: 3D fourth-order staggered-grid finite-difference schemes: Stability and grid dispersion. Bull. Seismol. Soc. Am. 90, 587–603 (2000). https://doi.org/10.1785/0119990119

    Article  Google Scholar 

  33. Moczo, P., Kristek, J.: On the rheological models used for time-domain methods of seismic wave propagation. Geophys. Res. Lett. 32 (2005) https://doi.org/10.1029/2004gl021598

  34. Moczo, P., Robertsson, J.O., Eisner, L.: The finite-difference time-domain method for modeling of seismic wave propagation. Adv. Geophys. 48, 421–516 (2007). https://doi.org/10.1016/S0065-2687(06)48008-0

    Article  Google Scholar 

  35. Pan, Y., Gao, L., Bohlen, T.: High-resolution characterization of near-surface structures by surface-wave inversions: From dispersion curve to full waveform. Surv. Geophys. 40, 167–195 (2019). https://doi.org/10.1007/s10712-019-09508-0

    Article  Google Scholar 

  36. Qiao, Z., Sun, C., Wu, D.: Theory and modelling of constant-Q viscoelastic anisotropic media using fractional derivative. Geophys. J. Int. 217, 798–815 (2019). https://doi.org/10.1093/gji/ggz050

    Article  Google Scholar 

  37. Robertsson, J.O., Blanch, J.O., Symes, W.W.: Viscoelastic finite-difference modeling. Geophysics 59, 1444–1456 (1994). https://doi.org/10.1190/1.1443701

    Article  Google Scholar 

  38. Sethi, H., Shragge, J., Tsvankin, I.: Mimetic finite-difference coupled-domain solver for anisotropic media. Geophysics 86(1), T45–T59 (2021). https://doi.org/10.1190/geo2020-0092.1

    Article  Google Scholar 

  39. Sethi, H., Shragge, J., Tsvankin, I.: Tensorial elastodynamics for coupled acoustic/elastic anisotropic media: Incorporating bathymetry. Geophys. J. Int. 228, 999–1014 (2022). https://doi.org/10.1093/gji/ggab374

    Article  Google Scholar 

  40. Sun, Y.C., Zhang, W., Chen, X.: 3D seismic wavefield modeling in generally anisotropic media with a topographic free surface by the curvilinear grid finite-difference method 3D seismic wavefield modeling in generally anisotropic media. Bull. Seismol. Soc. Am. 108, 1287–1301 (2018). https://doi.org/10.1785/0120170154

    Article  Google Scholar 

  41. Sun, Y.C., Zhang, W., Chen, X.: Seismic-wave modeling in the presence of surface topography in 2D general anisotropic media by a curvilinear grid finite-difference method. Bull. Seismol. Soc. Am. 106, 1036–1054 (2016). https://doi.org/10.1785/0120150285

    Article  Google Scholar 

  42. Sun, Y.C., Zhang, W., Ren, H., Bao, X., Xu, J.K., Sun, N., Yang, Z., Chen, X.: 3D seismic-wave modeling with a topographic fluid-solid Interface at the sea bottom by the curvilinear-grid finite-difference method. Bull. Seismol. Soc. Am. 111, 2753–2779 (2021). https://doi.org/10.1785/0120200363

    Article  Google Scholar 

  43. Sun, Y.C., Zhang, W., Xu, J.K., Chen, X.: Numerical simulation of 2-D seismic wave propagation in the presence of a topographic fluid–solid interface at the sea bottom by the curvilinear grid finite-difference method. Geophys. J. Int. 210, 1721–1738 (2017). https://doi.org/10.1093/gji/ggx257

    Article  Google Scholar 

  44. Tam, C.K., Webb, J.C.: Dispersion-relation-preserving finite difference schemes for computational acoustics. J. Comput. Phys. 107(2), 262–281 (1993). https://doi.org/10.1006/jcph.1993.1142

    Article  Google Scholar 

  45. Tarrass, I., Giraud, L., Thore, P.: New curvilinear scheme for elastic wave propagation in presence of curved topography. Geophys. Prospect. 59, 889–906 (2011). https://doi.org/10.1111/j.1365-2478.2011.00972.x

    Article  Google Scholar 

  46. Tromp, J., Komatitsch, D., Liu, Q.: Spectral-element and adjoint methods in seismology. Comm. Comput. Phys. 3, 1–32 (2008)

    Google Scholar 

  47. Vavryčuk V.: Asymptotic green’s function in homogeneous anisotropic viscoelastic media. Proc. Math. Phys. Eng. Sci. Proc. R. Soc. A-Math. Phys. 463, 2689–2707 (2007). https://doi.org/10.1098/rspa.2007.1862

  48. Virieux, J., Calandra, H., Plessix, R.É.: A review of the spectral, pseudo-spectral, finite-difference and finite-element modelling techniques for geophysical imaging. Geophys. Prospect. 59, 794–813 (2011). https://doi.org/10.1111/j.1365-2478.2011.00967.x

    Article  Google Scholar 

  49. Virieux, J., Operto, S.: An overview of full-waveform inversion in exploration geophysics. Geophysics 74, WCC1-WCC26 (2009). https://doi.org/10.1190/1.3238367

  50. Wang, N., Li, J., Borisov, D., Gharti, H.N., Shen, Y., Zhang, W., Savage, B.: Modeling three-dimensional wave propagation in anelastic models with surface topography by the optimal strong stability preserving Runge-Kutta method. J. Geophys. Res. Solid Earth 124, 890–907 (2019). https://doi.org/10.1029/2018JB016175

    Article  Google Scholar 

  51. Yang, P., Brossier, R., Métivier, L., Virieux, J.: A review on the systematic formulation of 3-D multiparameter full waveform inversion in viscoelastic medium. Geophys. J. Int. 207, 129–149 (2016). https://doi.org/10.1093/gji/ggw262

    Article  Google Scholar 

  52. Yang, Q., Zhou, B., Riahi, M.K., Al-Khaleel, M.: Frequency-domain seismic data transformation from point source to line source for 2D viscoelastic anisotropic media. Geophysics 87, T85–T98 (2022). https://doi.org/10.1190/geo2021-0166.1

    Article  Google Scholar 

  53. Yang, S. B., Zhou, B., Bai, C. Y.: A generalized 2.5-D Time-domain seismic wave equation to accommodate various elastic media and boundary conditions. Pure Appl. Geophys. 178, 2999–3025 (2021). https://doi.org/10.1007/s00024-021-02775-2

  54. Zhang, W., Chen, X.: Traction image method for irregular free surface boundaries in finite difference seismic wave simulation. Geophys. J. Int. 167, 337–353 (2006). https://doi.org/10.1111/j.1365-246X.2006.03113.x

    Article  Google Scholar 

  55. Zhou, B., Moosoo, W., Greenhalgh, S., Liu, X.: Generalized stiffness reduction method to remove the artificial edge effects for seismic wave modelling in elastic anisotropic media. Geophys. J. Int. 220(2), 1394–1408 (2020). https://doi.org/10.1093/gji/ggz529

    Article  Google Scholar 

  56. Zhou, B., Won, M., Jin, C.: New numerical schemes for time-domain seismic wave modeling in viscoelastic media. Second International Meeting for Applied Geoscience & Energy, 2384–2388 (2022). https://doi.org/10.1190/image2022-3751043.1

  57. Zhou, H.W., Hu, H., Zou, Z., Wo, Y., Youn, O.: Reverse time migration: A prospect of seismic imaging methodology. Earth-Sci. Rev. 179, 207–227 (2018). https://doi.org/10.1016/j.earscirev.2018.02.008

    Article  Google Scholar 

Download references

Acknowledgements

C. J. thanks the Chinese Scholarship Council and Khalifa University for the financial support.

Author information

Authors and Affiliations

  1. Department of Earth Science, Khalifa University of Science and Technology, 127788, Abu Dhabi, United Arab Emirates

    Chao Jin & Bing Zhou

  2. Department of Mathematics, Khalifa University of Science and Technology, 127788, Abu Dhabi, United Arab Emirates

    Mohamed Kamel Riahi

  3. Department of Electrical Engineering and Computer Science, Khalifa University of Science and Technology, 127788, Abu Dhabi, United Arab Emirates

    Mohamed Jamal Zemerly

Authors
  1. Chao Jin
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Bing Zhou
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Mohamed Kamel Riahi
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Mohamed Jamal Zemerly
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Chao Jin.

Ethics declarations

Competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Jin, C., Zhou, B., Riahi, M.K. et al. A generalized time-domain velocity-stress seismic wave equation for composite viscoelastic media with a topographic relief and an irregular seabed. Comput Geosci (2024). https://doi.org/10.1007/s10596-024-10273-2

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s10596-024-10273-2

Keywords

Search

Navigation