Skip to main content
SpringerLink
Log in

Quantitative production analysis and EUR prediction from unconventional reservoirs using a data-driven drainage volume formulation

  • Original Paper
  • Published:
Computational Geosciences Aims and scope Submit manuscript

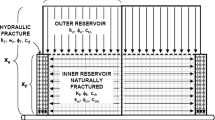
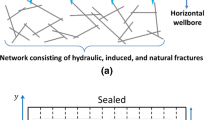
Abstract

A novel data-driven approach was previously introduced for production analysis of unconventional reservoirs without the traditional rate transient analysis/pressure transient analysis assumptions. The approach relied on a w(τ) function, which is drainage volume geometry function to characterize the flow geometry from the transient drainage volume. It has been used to rank refracturing candidates and to determine optimal fracture spacing. In this paper, we generalize the previous study to improve the amount of quantitative reservoir information obtained during the production analysis. Our approach is based upon a transient generalization of the Matthews-Brons-Hazebroek definition of the pseudo-steady state drainage volume. It is obtained from an asymptotic solution of the diffusivity equation in heterogeneous and/or fractured media. Given field pressure and flow rate data, we can calculate the transient well drainage volume with time. The time evolution of the drainage volume can be inverted to estimate w(τ) function, which contains information of underlying flow geometries, and which is then used for quantitative analysis. The power and utility of the proposed methodology is first validated with synthetic examples and then demonstrated using a well from the Montney shale. In the examples studied, we are able to identify linear flow, the onset of fracture interference, complex nonlinear flow, and the development of the stimulated reservoir volume (SRV), leading to the quantitative calculation of matrix permeability, fracture surface area, and volume of the SRV. The proposed approach is a data-driven model-free analysis of production data without the presumption of specific flow regimes. It provides a simple and intuitive understanding of the transient drainage volume and instantaneous recovery efficiency, irrespective of the complexity of the reservoir depletion geometry. We show an improved approach for the w(τ) inversion which yields better physical resolution and which can identify more detailed characteristics of the underlying flow geometry than previous studies, e.g., complex near-fracture flow, linear flow, and fracture interference. The results of the analysis have been used for the characterization of hydraulic fracture and reservoir properties, including the prediction of fracture surface area, matrix permeability, and SRV, and extended to the calculation of estimated ultimate recovery.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Abbreviations

A :

Cross-sectional area (ft2)

An(t):

Pressure amplitude of the n th order in the time domain (1 /h(n+ 2)/2)

\(\tilde {A_{n}}(\vec {{x}})\) :

Pressure amplitude of the n th order in the frequency domain (1 /h(n+ 2)/2)

b :

Decline curve exponent (dimensionless)

\(\bar {{B}}_{\mathrm {g}} \) :

Average gas formation volume factor (Mcf /Mscf)

c t :

Total compressibility (1 /psi)

\(\bar {{c}}_{t} \) :

Average total compressibility (1 /psi)

D :

Decline rate (1 /h)

h :

Payzone thickness (ft)

i :

Imaginary unit

J :

Well productivity (stb /psi / day)

J BDF :

Well productivity under boundary- dominated flow (stb /psi / day)

J PSS :

Well productivity under pseudo-steady state (stb /psi / day)

k :

Permeability (md)

k f :

Fracture permeability (md)

k m :

Matrix permeability (μ d)

K (τ,t):

Diffusion kernel

L res :

Reservoir length (ft)

L w :

Well lateral length (ft)

n basis :

Number of basis functions

n data :

Number of data points in the interval

n f :

Number of hydraulic fractures

n t :

Number of data points in the production history

p :

Pressure (psi)

\(\bar {{p}}\) :

Average pressure (psi)

\(\tilde {{p}}\) :

Pressure in frequency domain (psi)

p a :

Adjusted pressure for gas (psi)

p wf :

Bottomhole flowing pressure (psi)

q :

Flux (stb /day)

q sf :

Flux at sandface (stb /day)

q w :

Flux at surface (stb /day)

q w, cutoff :

Cutoff production rate at surface (Mscf /day)

Q w :

Cumulative production (ft3)

r :

Distance (ft)

r res :

Reservoir radius (ft)

r w :

Wellbore radius (ft)

RNPm,n :

RNP induced at fracture m by fracture n (stb /psi / day)

S :

Skin (dimensionless)

S w :

Water saturation (fraction)

t :

Time (h)

t a :

Adjusted time for gas (h)

t e :

Material balance time (h)

t elf :

Time of end of linear flow (h)

t h :

Production history used for w(τ) inversion (day)

t LOD :

Time to detect round-trip pressure front propagation under LOD (day)

t prod :

Production period (day)

t (a /2,dof):

Student’s t distribution with confidence level (a) and degree of freedom (dof)

T res :

Reservoir temperature (∘F)

V (t):

Generalized time-dependent volume integral (ft3)

V (τ,t):

Generalized incomplete volume integral (ft3)

Vd(t):

Drainage volume (ft3)

V det :

Reservoir pore volume detected during inversion (ft3)

Vp(τ):

Pore volume (ft3)

V res :

Reservoir volume (ft3)

w(τ):

Derivative of pore volume with respect to τ (ft3 /h1/2)

w f :

Fracture width (in)

w res :

Reservoir width (ft)

W(t):

Generalized pressure drop integral (h)

W (τ,t):

Generalized incomplete pressure drop integral (h)

\(\vec {x}\) :

Cartesian spatial coordinate vector

x f :

Fracture half length (ft)

x s :

Fracture spacing (ft)

X (t):

Generalized average pressure drop integral (ft3/h)

X (τ,t):

Generalized incomplete average pressure drop integral (ft3/h)

\(\hat {{y}}\) :

Data estimate from linear regression analysis

α :

Hydraulic diffusivity (ft2 /h)

α k :

Coefficient of the k th basis function

Δp :

Pressure drop (in time) (psi)

Δpm,n :

Pressure drop induced at fracture m by fracture n (psi)

Δp′ :

Well-test derivative (psi)

λ :

Weight of the roughness penalty term

μ :

Fluid viscosity (cp)

\(\bar {{\mu } }_{\mathrm {g}} \) :

Average gas viscosity (cp)

ξ :

Boltzmann variable (dimensionless)

ξ DOI :

Depth of investigation in terms of the Boltzmann variable (dimensionless)

τ :

Diffusive time of flight (h1/2)

τ DOI :

Depth of investigation in terms of the diffusive time of flight (h1/2)

τ fs :

Fracture spacing in terms of the diffusive time of flight (h1/2)

τ LOD :

Limit of detectability in terms of the diffusive time of flight (h1/2)

τ det :

Diffusive time of flight detected during inversion (h1/2)

τ max :

Upper limit of diffusive time of flight during inversion (h1/2)

τ w :

Diffusive time of flight at wellbore radius (h1/2)

τ wf :

Diffusive time of flight at effective radius (h1/2)

τ res :

Diffusive time of flight at reservoir boundary (h1/2)

ϕ :

Porosity (fraction)

ϕk (τ):

The k th basis function

ω :

Frequency of the asymptotic expansion (s− 1)

1-D:

one-dimensional

3-D:

three-dimensional

BDF:

boundary-dominated flow

BLF:

bounded linear flow

BU:

buildup

DOI:

depth of investigation

DTOF:

diffusive time of flight

EUR:

estimated ultimate recovery

FMM:

fast marching method

HF:

hydraulic fracture

LOD:

limit of detectability

MFSS:

modified Friedman’s super smoother

MLRA:

moving linear regression analysis

MTFW:

multiple transverse fracture well

ODE:

ordinary differential equation

PPSS:

pseudo pseudo-steady state

PSS:

pseudo-steady state

PTA:

pressure transient analysis

PV:

pore volume

RNP:

rate-normalized pressure drop

RTA:

rate transient analysis

SRV:

stimulated reservoir volume

UR:

ultimate recovery

References

  1. Arps, J.J.: Analysis of decline curves. Trans. AIME 160(1). https://doi.org/10.2118/945228-G (1945)

  2. Datta-Gupta, A., King, M.J.: Streamline Simulation: Theory and Practice. Society of Petroleum Engineers, Richardson (2007). Original edition. ISBN 978-1555631116

    Google Scholar 

  3. Fetkovich, M.J.: Decline curve analysis using type curves. https://doi.org/10.2118/4629-PA (1980)

  4. Friedman, J.H.: A Variable Span Smoother. Laboratory for Computational Statistics (1984)

  5. Green, P.J., Silverman, B.W.: Nonparametric Regression and Generalized Linear Models a Roughness Penalty Approach. Chapman and Hall/CRC, Boca Raton (1994). Original edition. ISBN 978-0-412-30040-0

    Book  Google Scholar 

  6. Holditch, S.A.: Unconventional oil and gas resource development—let’s do it right. J. Unconventional Oil Gas Resources 1–2, 2–8 (2013). https://doi.org/10.1016/j.juogr.2013.05.001

    Article  Google Scholar 

  7. Jensen, J.L., Lake, L.W., Corbett, P.W.M., et al.: Statistics for Petroleum Engineers and Geoscientists. Prentice Hall PTR, Upper Saddle River (1997). Original edition. ISBN 978-0131318557

    Google Scholar 

  8. King, M.J., Wang, Z., Datta-Gupta, A.: Asymptotic solutions of the diffusivity equation and their applications. In: SPE Europec Featured at 78th EAGE Conference and Exhibition, Vienna, Austria, 30 May–2 June 2016. Society of Petroleum Engineers. https://doi.org/10.2118/180149-MS (2016)

  9. Kuchuk, F.J.: Radius of Investigation for Reserve Estimation from Pressure Transient Well Tests. Society of Petroleum Engineers. https://doi.org/10.2118/120515-MS (2009)

  10. Kulkarni, K.N., Datta-Gupta, A., Vasco, D.W.: A streamline approach for integrating transient pressure data into high-resolution reservoir models. https://doi.org/10.2118/74135-PA (2001)

  11. Lee, J., Rollins, J.N., Spivey, J.P.: Pressure Transient Testing. Society of Petroleum Engineers, Richardson (2003). Original edition. ISBN 978-1555630997

    Google Scholar 

  12. Malone, A., King, M.J., Wang, Z.: Characterization of multiple transverse fractured wells using the asymptotic approximation of the diffusivity equation. In: SPE Europec Featured at the 81st EAGE Conference and Exhibition, London, England, UK, 3–6 June 2019. Society of Petroleum Engineers (2019)

  13. Matthews, C.S., Brons, F., Hazebroek, P.: A method for determination of average pressure in a bounded reservoir. Pet. Trans. 201, 182–191 (1954)

    Google Scholar 

  14. Ramsay, J.O., Hooker, G., Graves, S.: Functional Data Analysis with R and MATLAB. Springer Science + Business Media, LLC, New York (2009). Original edition. ISBN 978-0-387-98184-0

    Book  Google Scholar 

  15. Sethian, J.: Fast marching methods. SIAM Rev. 41(2), 199–235 (1999)

    Article  Google Scholar 

  16. Song, B., Ehlig-Economides, C.A.: Rate-normalized pressure analysis for determination of shale gas well performance. North American Unconventional Gas Conference and Exhibition. Society of Petroleum Engineers. https://doi.org/10.2118/144031-MS (2011)

  17. Vasco, D.W., Keers, H., Karasaki, K.: Estimation of reservoir properties using transient pressure data: an asymptotic approach. Water Resour. Res. 36(12), 3447–3465 (2000)

  18. Virieux, J., Flores-Luna, C., Gibert, D.: Asymptotic theory for diffusive electromagnetic imaging. Geophys. J. Int. 119(3), 857–868 (1994)

    Article  Google Scholar 

  19. Wang, Z., Li, C., King, M.: Validation and Extension of Asymptotic Solutions of Diffusivity Equation and Their Applications to Synthetic Cases. Society of Petroleum Engineers. https://doi.org/10.2118/182716-MS (2017)

  20. Wang, Z., Malone, A., King, M.J.: Quantitative production analysis and EUR prediction from unconventional reservoirs using a data-driven drainage volume formulation. EAGE, Barcelona (2018)

    Book  Google Scholar 

  21. Wattenbarger, R.A., El-Banbi, A.H., Villegas, M.E., et al.: Production analysis of linear flow into fractured tight gas wells. In: SPE Rocky Mountain Regional/Low-Permeability Reservoirs Symposium, Denver, Colorado, 5–8 April 1998. Society of Petroleum Engineers. https://doi.org/10.2118/39931-MS (1998)

  22. Xue, X., Yang, C., Sharma, V.K., et al: Reservoir and fracture flow characterization using a novel W(τ) formulation. In: SPE/AAPG/SEG Unconventional Resources Technology Conference, San Antonio, Texas, 1–3 August 2016. Unconventional Resources Technology Conference. https://doi.org/10.15530/URTEC-2016-2440083 (2016)

  23. Yang, C., Sharma, V.K., Datta-Gupta, A., et al: A novel approach for production transient analysis of shale gas/oil reservoirs. In: Unconventional Resources Technology Conference, San Antonio, Texas, 20–22 July 2015. Unconventional Resources Technology Conference. https://doi.org/10.15530/URTEC-2015-2176280 (2015)

  24. Zhang, Y., Yang, C., King, M.J., et al.: Fast-Marching Methods for Complex Grids and Anisotropic Permeabilities: Application to Unconventional Reservoirs. Society of Petroleum Engineers. https://doi.org/10.2118/163637-MS (2013)

Download references

Acknowledgments

The authors would like to acknowledge the support of Energi Simulation (formerly Foundation CMG) through the Texas A&M chair in Robust Reduced Complexity Modeling with Dr. Eduardo Gildin and the support of the members of the MCERI joint industry project at Texas A&M University.

Author information

Authors and Affiliations

  1. Texas A&M University, Richardson Building, Room 703, College Station, TX, 77840, USA

    Zhenzhen Wang, Andrew Malone & Michael J. King

  2. Chevron ETC, 1500 Louisiana ST, Houston, TX, 77002, USA

    Zhenzhen Wang

Authors
  1. Zhenzhen Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Andrew Malone
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Michael J. King
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Zhenzhen Wang.

Additional information

Publisher’s note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Wang, Z., Malone, A. & King, M.J. Quantitative production analysis and EUR prediction from unconventional reservoirs using a data-driven drainage volume formulation. Comput Geosci 24, 853–870 (2020). https://doi.org/10.1007/s10596-019-09833-8

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10596-019-09833-8

Keywords

Search

Navigation