Abstract
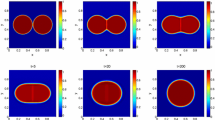
In this paper, we propose an energy-stable evolution method for the calculation of the phase equilibria under given volume, temperature, and moles (VT-flash). An evolution model for describing the dynamics of two-phase fluid system is based on Fick’s law of diffusion for multi-component fluids and the Peng-Robinson equation of state. The mobility is obtained from diffusion coefficients by relating the gradient of chemical potential to the gradient of molar density. The evolution equation for moles of each component is derived using the discretization of diffusion equations, while the volume evolution equation is constructed based on the mechanical mechanism and the Peng-Robinson equation of state. It is proven that the proposed evolution system can well model the VT-flash problem, and moreover, it possesses the property of total energy decay. By using the Euler time scheme to discretize this evolution system, we develop an energy stable algorithm with an adaptive choice strategy of time steps, which allows us to calculate the suitable time step size to guarantee the physical properties of moles and volumes, including positivity, maximum limits, and correct definition of the Helmhotz free energy function. The proposed evolution method is also proven to be energy-stable under the proposed time step choice. Numerical examples are tested to demonstrate efficiency and robustness of the proposed method.
Similar content being viewed by others
References
Cogswell, D.A.: A phase-field study of ternary multiphase microstructures. PhD thesis, MIT USA (2010)
Firoozabadi, A.: Thermodynamics of hydrocarbon reservoirs McGraw-Hill New York (1999)
Jindrová, T., Mikyška, J.: Fast and robust algorithm for calculation of two-phase equilibria at given volume, temperature, and moles. Fluid Phase Equilib 353, 101–114 (2013)
Kou, J., Sun, S., Wang, X.: Efficient numerical methods for simulating surface tension of multi-component mixtures with the gradient theory of fluid interfaces. Comput. Methods Appl. Mech. Eng. 292, 92–106 (2015)
Kou, J., Sun, S.: Numerical methods for a multi-component two-phase interface model with geometric mean influence parameters. SIAM J. Sci. Comput. 37(4), B543–B569 (2015)
Kou, J., Sun, S.: Unconditionally stable methods for simulating multi-component two-phase interface models with Peng-Robinson equation of state and various boundary conditions. J. Comput. Appl. Math. 291(1), 158–182 (2016)
Lake, L.W.: Fundamentals of enhanced oil recovery Society of Petroleum Engineers (1986)
Michelsen, M.L.: The isothermal flash problem. part i. stability. Fluid Phase Equilib. 9(1), 1–19 (1982)
Michelsen, M.L.: The isothermal flash problem. part ii. phase-split calculation. Fluid Phase Equilib. 9(1), 21–40 (1982)
Michelsen, M.L., Mollerup, J.M.: Thermodynamic models: fundamentals & computational aspects Tie-Line Publications Denmark (2004)
Mikyška, J., Firoozabadi, A.: A new thermodynamic function for phase-splitting at constant temperature, moles, and volume. AIChE J 57(7), 1897–1904 (2011)
Mikyška, J., Firoozabadi, A.: Investigation of mixture stability at given volume, temperature, and number of moles. Fluid Phase Equilib. 321, 1–9 (2012)
Jindrová, T., Mikyška, J.: General algorithm for multiphase equilibria calculation at given volume, temperature, and moles. Fluid Phase Equilib. 393, 7–25 (2015)
Miqueu, C., Mendiboure, B., Graciaa, C., Lachaise, J.: Modelling of the surface tension of binary and ternary mixtures with the gradient theory of fluid interfaces. Fluid Phase Equilib. 218, 189–203 (2004)
Peng, D., Robinson, D.B.: A new two-constant equation of state. Ind. Eng. Chem. Fundam. 15(1), 59–64 (1976)
Polívka, O., Mikyška, J.: Compositional modeling in porous media using constant volume flash and flux computation without the need for phase identification. J. Comput. Phys. 272, 149–169 (2014)
Qiao, Z., Sun, S.: Two-phase fluid simulation using a diffuse interface model with Peng-Robinson equation of state. SIAM J. Sci. Comput. 36(4), B708–B728 (2014)
Sun, S., Wheeler, M.F.: Symmetric and nonsymmetric discontinuous Galerkin methods for reactive transport in porous media. SIAM J. Numer. Anal. 43(1), 195–219 (2005)
Sun, S., Firoozabadi, A., Kou, J.: Numerical modeling of two-phase binary fluid mixing using mixed finite elements. Comput. Geosci. 16, 1101–1124 (2012)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Kou, J., Sun, S. & Wang, X. An energy stable evolution method for simulating two-phase equilibria of multi-component fluids at constant moles, volume and temperature. Comput Geosci 20, 283–295 (2016). https://doi.org/10.1007/s10596-016-9564-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10596-016-9564-5